菜鸟追梦旅行

这个屌丝很懒，什么也没留下！

热门标签

LLM高效参数微调方法：从Prefix Tuning、Prompt Tuning、P-Tuning V1/V2到LoRA、QLoRA(含对模型量化的解释)_llm微调

作者：菜鸟追梦旅行 | 2024-03-21 01:58:45

踩

llm微调

前言

学过大模型的都知道，PEFT 方法仅微调少量(额外)模型参数，同时冻结预训练 LLM 的大部分参数，比如Prefix Tuning、P-Tuning V1/V2、LoRA、QLoRA，其实网上介绍这些微调方法的文章/教程不少了，我也看过不少，但真正写的一目了然、一看就懂的还是少，大部分文章/教程差点意思

总之，把知识写清楚、讲清楚并不容易，比如“把知识写清楚”的这个能力我从2010年起，算练了10多年了，如今依然热衷于把知识真正写清晰化，加之今年一直在不断深入大模型相关的技术，写了各种模型的微调，但之前还没好好总结过各类微调方法，而微调方法很重要，故成此文

第一部分微调发展简史：Adapter Tuning、PET、Prefix Tuning

1.1 Google之Adapter Tuning：嵌入在transformer里原有参数不变只微调新增的Adapter

谷歌的研究人员于2019年在论文《Parameter-Efficient Transfer Learning for NLP》提出针对 BERT 的 PEFT 微调方式，拉开了 PEFT 研究的序幕。他们指出

在面对特定的下游任务时，如果进行 Full-fintuning（即预训练模型中的所有参数都进行微调），太过低效
而如果采用固定预训练模型的某些层，只微调接近下游任务的那几层参数，又难以达到较好的效果

于是他们设计了如下图所示的 Adapter 结构

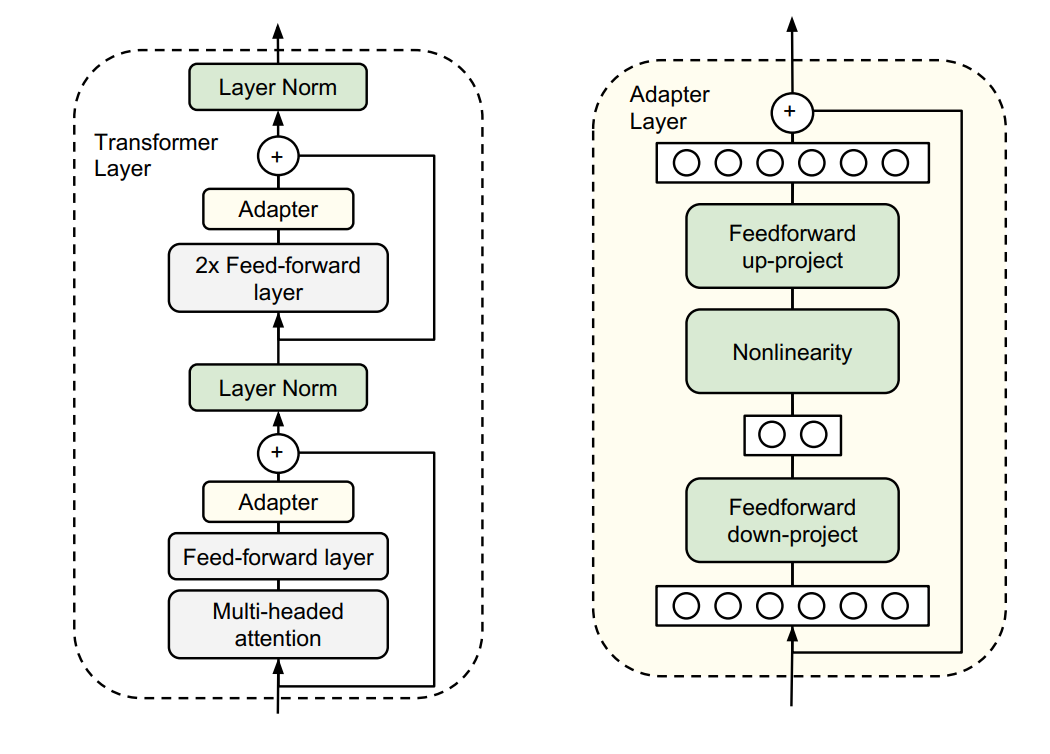
如上图左侧所示，将其嵌入 Transformer 的结构里面，在训练时，固定住原来预训练模型的参数不变，只对新增的 Adapter 结构进行微调
如上图右侧所示，同时为了保证训练的高效性（也就是尽可能少的引入更多参数），他们将 Adapter 设计为这样的结构：
首先是一个 down-project 层将高维度特征映射到低维特征，然后过一个非线形层之后，再用一个 up-project 结构将低维特征映射回原来的高维特征；
同时也设计了 skip-connection 结构，确保了在最差的情况下能够退化为 identity

从实验结果来看，该方法能够在只额外对增加的3.6%参数规模（相比原来预训练模型的参数量）的情况下取得和Full-finetuning接近的效果（GLUE指标在0.4%以内）

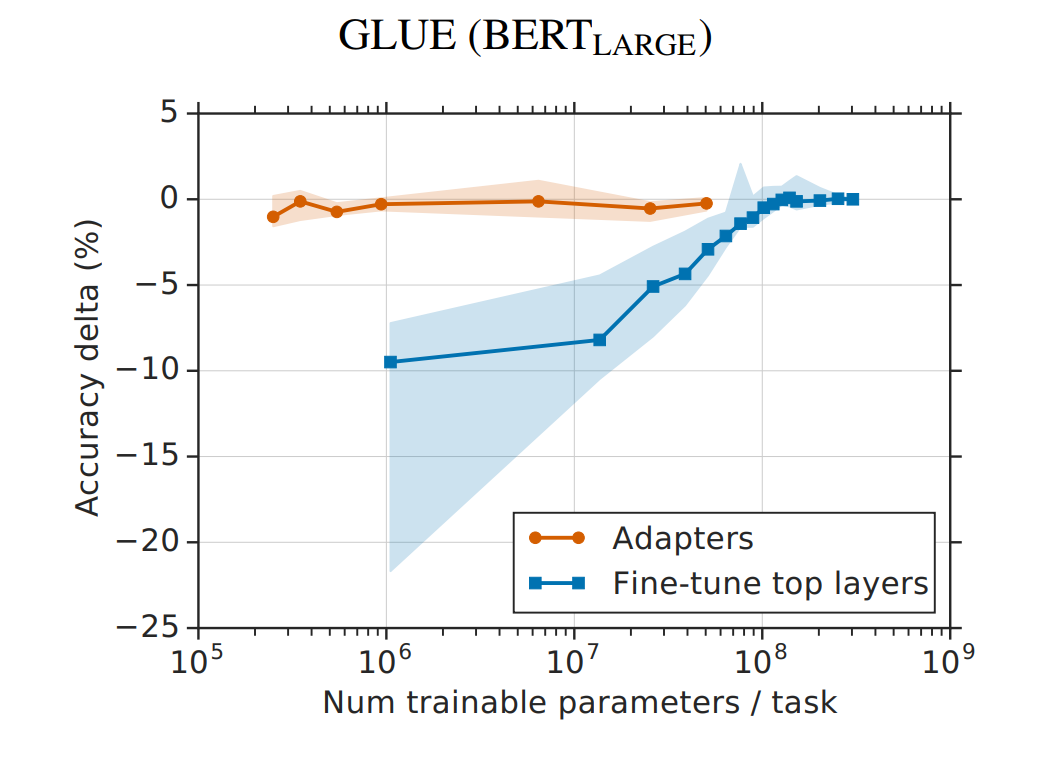
1.2 Pattern-Exploiting Training：人工构建离散模板

想要更好的理解下文将讲的prefix-tuning/P-Tuning，便不得不提Pattern-Exploiting Training(PET)，所谓PET，主要的思想是借助由自然语言构成的模版(英文常称Pattern或Prompt)，将下游任务也转化为一个完形填空任务，这样就可以用BERT的MLM模型来进行预测了。比如下图中通过条件前缀来实现情感分类和主题分类的例子(下图来自参考文献7)：

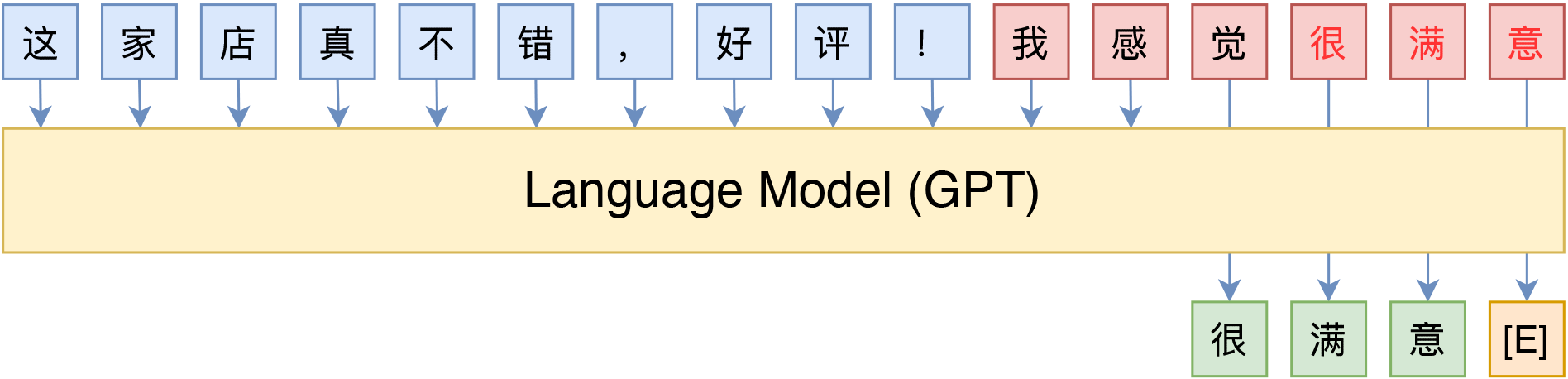
当然，这种方案也不是只有MLM模型可行，用GPT这样的单向语言模型（LM）其实也很简单：

不过由于语言模型是从左往右解码的，因此预测部分只能放在句末了(但还可以往补充前缀说明，只不过预测部分放在最后)

某种意义上来说，这些模版属于语言模型的“探针”，我们可以通过模版来抽取语言模型的特定知识，从而做到不错的零样本效果，而配合少量标注样本，可以进一步提升效果

然而，对于某些任务而言，人工构建模版并不是那么容易的事情，模型的优劣我们也不好把握，而不同模型之间的效果差别可能很大。所以，如何根据已有的标注样本来自动构建模版，便成了一个值得研究的问题了

1.3 斯坦福之Prefix Tuning：通过virtual token构造连续型隐式prompt

在prefix-tuning之前的工作主要是人工设计离散的template或者自动化搜索离散template，问题在于最终的性能对人工设计的template的特别敏感：加一个词或者少一个词，或者变动位置，都会造成很大的变化，所以这种离散化的token的搜索出来的结果可能并不是最优的

因此斯坦福的研究人员Xiang Lisa Li, Percy Liang等人于2021年年初通过此论文《Prefix-Tuning：Optimizing Continuous Prompts for Generation》提出Prefix Tuning方法，其使用连续的virtual token embedding来代替离散的token，且与Full-finetuning更新所有参数的方式不同，如下图所示(注意体会图中fine-tuning与prefix tuning的区别)

该方法是在输入token之前构造一段任务相关的virtual tokens作为Prefix
相当于对于transformer的每一层 (不只是输入层，且每一层transformer的输入不是从上一层输出，而是随机初始化的embedding作为输入)，都在真实的句子表征前面插入若干个连续的可训练的"virtual token" embedding，这些伪token不必是词表中真实的词，而只是若干个可调的自由参数

为了形象说明，举个例子，对于table-to-text任务，context $x$ 是序列化的表格，输出 $y$ 是表格的文本描述，使用GPT-2进行生成；对于文本摘要， $x$ 是原文， $y$ 是摘要，使用BART进行生成
$\rightarrow$ 对于自回归(Autoregressive)模型，在句子前面添加前缀，得到 $z=[P R E F I X ; x ; y]$
这是因为合适的上文能够在fixed LM的情况下去引导生成下文（比如GPT3的 in-context learning）
$\rightarrow$ 对Encoder-Decoder模型来说，Encoder和Decoder都增加了前缀，得到 $z=\left[P R E F I X ; x \mid P R E F I X^{\prime} ; y\right]$
这是因为Encoder端增加前缀是为了引导输入部分的编码 (guiding what to extract from $x$ )，Decoder 端增加前缀是为了引导后续token的生成 (influence the generation of $y$ by steering the next token distribution)
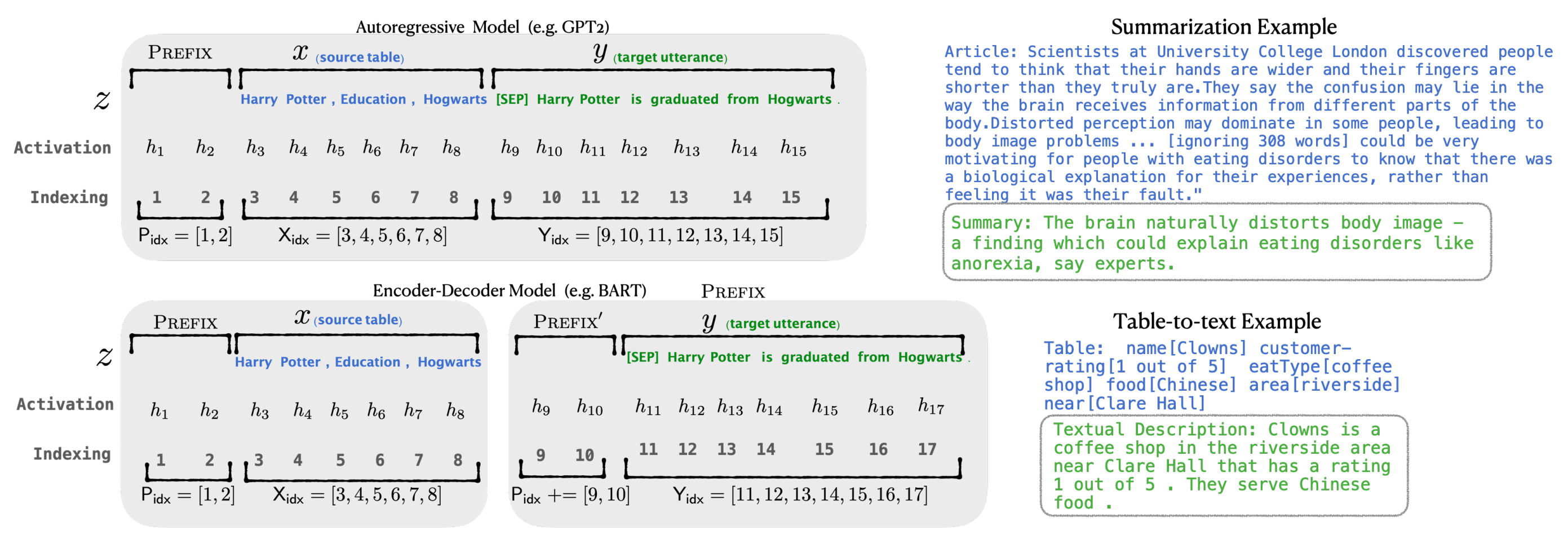
然后训练的时候只更新Prefix部分的参数，而Transformer中的预训练参数固定

对于上述这个过程，有以下几点值得注意

该方法其实和构造Prompt类似，只是Prompt是人为构造的“显式”的提示，并且无法更新参数，而Prefix则是可以学习的“隐式”的提示
同时，为了防止直接更新Prefix的参数导致训练不稳定的情况，特在Prefix层前面加了MLP结构(相当于将Prefix分解为更小维度的Input与MLP的组合后输出的结果)，训练完成后，只保留Prefix的参数
prefix-prompt的效果优于adapter tuning 和 finetune最上面的两层，最终和全参数finetune差不多，且在低资源情况下，效果优于finetune
更长的前缀意味着更多的可微调参数，效果也变好，不过长度还是有阈值限制的(table-to-text是10，summarization是200)
可调参数作为前缀： $[P R E F I X ; x ; y]$ ，比作为中缀 $[x ; I N F I X, y]$ 更好一点。毕竟对于自回归模型，每个位置只能关注到它之前的位置，那么中缀中的 $x$ 其实是关注不到INFIX的

第二部分 Prompt Tuning

还是2021年4月，Google Research通过此篇论文《The Power of Scale for Parameter-Efficient Prompt Tuning》提出了Prompt Tuning(该论文4月首次提交，后于当年9月提交V2版本)

该方法可以看做是21年年初提出的Prefix Tuning的简化版本「Our method can be seenas a simplification of the recently proposed“prefix tuning” of Li and Liang (2021)」

对于prefix tuning，其 learning a sequence of prefixes that are prepended at every transformer layer. This is akin to learning transformer activations that are fixed across exam-ples at every network layer
相比之下，prompt tuning使用单个提示表示，该表示前置于嵌入式输入。除了需要更少的参数外，所提出方法允许transformer更新中间层任务表示，通过输入示例进行上下文化
In contrast, prompt tuning uses a single prompt representation thatis prepended to the embedded input. Beyond re-quiring fewer parameters, our approach allows thetransformer to update the intermediate-layer taskrepresentations, as contextualized by an input ex-ample
且When using BART, prefix tuning includes prefixes on both the encoder and decoder network,while prompt tuning only requires prompts on the encoder

此外，Li和Liang(2021)提出的prefix tuning也依赖于前缀的重新参数化来稳定学习，这在训练期间增加了大量参数，而prompt tuning的配置不需要这种重新参数化，并且在SuperGLUE任务和模型尺寸上都是鲁棒的
Li and Liang (2021) also rely on a repa-rameterization of the prefix to stabilize learning,which adds a large number of parameters duringtraining, where as our configuration does not re-quire this reparameterization and is robust acrossSuperGLUE tasks and model size
它冻结整个预训练模型，只允许每个下游任务在输入文本前添加额外的k个可调tokens(意味着它给每个任务都定义了自己的Prompt，在输入层加入prompt tokens，即We freeze the entire pre-trained model and only al-low an additional k tunable tokens per downstreamtask to be prepended to the input text)

具体而言，如下图所示

Model tuning需要为每个下游任务生成整个预训练模型的任务特定副本，并且推理必须分批执行
Model tuning requires making a task-specific copy of the entire pre-trained model for eachdownstream task and inference must be performed inseparate batches
Prompt tuning只需要为每个任务存储一个小的特定于任务的提示，并使用原始的预训练模型支持混合任务推理
Prompt tuning only requires stor-ing a small task-specific prompt for each task, andenables mixed-task inference using the original pre-trained model

对于T5“XXL”模型，对tuned model而言，每个副本需要110亿个参数，相比之下，对tuned prompts而言，每个任务只需要20,480个参数—假设提示长度为5个tokens，则减少了5个数量级以上(With a T5 “XXL” model, each copyof the tuned model requires 11 billion parameters. Bycontrast, our tuned prompts would only require 20,480parameters per task—a reduction of over five orders ofmagnitude—assuming a prompt length of 5 tokens)

且通过实验发现，随着预训练模型参数量的增加，Prompt Tuning的方法会逼近全参数微调的结果

第三部分 P-Tuning V1/V2

3.1 P-Tuning V1：将自然语言的离散模版转化为可训练的隐式prompt (连续参数优化问题)

清华大学的研究者于2021年3月通过此篇论文《GPT Understands, Too》提出P-Tuning，其与prefix tuning类似：比如考虑到神经网络本质上是连续的，故离散提示可能不是最优的(sinceneural networks are inherently continuous, discrete promptscan be sub-optimal )，从而也采取连续的提示

总之，P-Tuning成功地实现了模版的自动构建，且借助P-tuning，GPT在SuperGLUE上的成绩首次超过了同等级别的BERT模型，这颠覆了在那年之前“GPT不擅长NLU”的结论，也是该论文命名的缘由

P-tuning和prefix tuning类似，也放弃了“模版由自然语言构成”这一常规要求，从而将模版的构建转化为连续参数优化问题

下图是一个prompt search针对“The capital of Britain is [MASK]”(英国的首都是哪个城市)的例子
即给定上下文(蓝色区域，“英国”)和目标(红色区域，“[MASK]”)，橙色区域指的是提示符号prompt tokens

在(a)中，提示生成器只收到离散的奖励
In (a), the prompt generator only receives discrete rewards
在(b)中，伪prompt和prompt encoder可以以可微的方式进行优化，有时，在(b)中添加少量与任务相关的anchor tokens(如“capital”)将带来进一步的改进
in (b) the pseudo prompts and prompt encoder can be optimized in a differentiable way. Sometimes, adding few task-related anchor tokens(such as “capital” in (b)) will bring further improvement

换言之，P-tuning做法是用一些伪prompt代替这些显式的prompt (说白了，将自然语言提示的token，替换为可训练的嵌入)
具体的做法是可以用预训练词表中的unused token作为伪prompt「BERT的vocab里有unused 1 ~ unused99，就是为了方便增加词汇的」，然后通过训练去更新这些token的参数
也就是，P-tuning的prompt Prompt不是显式的，不是我们可以看得懂的字符，而是一些隐式的、经过训练的、模型认为最好的prompt token

但相比prefix-tuning

P-Tuning加了可微的virtual token，但是仅限于输入，没有在每层加
且virtual token的位置也不一定是前缀，插入的位置是可选的，这里的出发点实际是把传统人工设计模版中的真实token替换成可微的virtual token

优化virtual token的挑战：经过预训练的LM的词嵌入已经变得高度离散，如果随机初始化virtual token，容易优化到局部最优值；这些virtual token理论是应该有相关关联的，如何建模这种关联也是问题
当然实际在实验中，作者发现的是用一个prompt encoder来编码收敛更快，效果更好。也就是说，用一个LSTM+MLP去编码这些virtual token以后，再输入到模型「And in practice, we choose a bidi-rectional long-short term memory networks (LSTM), with a ReLU activated two-layer multilayer perceptron (MLP) toencourage discreteness. Formally speaking, the real inputembeddings $\mathrm{h}_{\mathrm{i}}^{0}$ to the language model M is derived from」
换言之，P-tuning并不是随机初始化几个新token然后直接训练的，而是通过一个小型的LSTM模型把这几个Embedding算出来，并且将这个LSTM模型设为可学习的
$\begin{aligned} h_{i} & =\operatorname{MLP}\left(\left[\overrightarrow{h_{i}}: \overleftarrow{h_{i}}\right]\right) \\ & =\operatorname{MLP}\left(\left[\operatorname{LSTM}\left(h_{0: i}\right): \operatorname{LSTM}\left(h_{i: m}\right)\right]\right) \end{aligned}$

所以说，当预训练模型足够大的时候，可能无法finetune整个模型，而P-tuning可以选择只优化几个Token的参数，因为优化所需要的显存和算力都会大大减少，所以P-tuning实则上给了我们一种在有限算力下调用大型预训练模型的思路

且如苏剑林所说：“在P-tuning中，如果我们不将新插入的token视为“模版”，是将它视为模型的一部分，那么实际上P-tuning也是一种类似Adapter的做法，同样是固定原模型的权重，然后插入一些新的可优化参数，同样是只优化这些新参数，只不过这时候新参数插入的是Embedding层，因此，从这个角度看，P-tuning与Adapter有颇多异曲同工之处”

3.2 P-Tuning V2：在输入前面的每层加入可微调的参数

然P-tuning依然在下面两点上有其对应的局限

规模通用性：在Fixed LM Prompt Tuning并采用全量数据的前提下，Prompt Tuning (The Power of Scale for Parameter-Efficient Prompt Tuning) 被证明能够匹敌Fine-tuning的效果，而只需要很少的参数微调：但是要求是10B以上的参数量的预训练模型，以及特殊的初始化技巧等
对于普通模型，能不能在Fixed LM Prompt Tuning+全量数据情况下匹敌Fine-tuning？
任务通用性：尽管P-tuning在SuperGLUE上表现很好，对于一些比较难的token-level的任务表现就差强人意了，比如阅读理解和NER，当然现在也有一些工作在用prompt做序列标注（template-NER，lightNER，template-free NER）
还有一个问题是，不是所有标签都有明确的语义，verbalizer这边映射的label words都是有具体含义的，对于一些没有label语义的分类任务应该怎么办，比如用户评论的聚类等

为了解决上面两个痛点，发表于2022年的此篇论文《P-Tuning v2: Prompt Tuning Can Be Comparable to Fine-tuning Universally Across Scales and Tasks》提出了P-tuning的V2版本

其有以下几个特点

Deep Prompt Tuning on NLU
采用Prefix-tuning的做法，在输入前面的每层加入可微调的参数
去掉重参数化的编码器
以前的方法利用重参数化功能来提高训练速度和鲁棒性（例如，用于prefix-tunning的 MLP 和用于 P-tuning的 LSTM）。在 P-tuning v2 中，作者发现重参数化的改进很小，尤其是对于较小的模型，同时还会影响模型的表现
可选的多任务学习
Deep Prompt Tuning的优化难题可以通过增加额外的任务数据或者无标注数据来缓解，同时可微调的prefix continuous prompt也可以用来做跨任务的共享知识。比如说，在NER中，可以同时训练多个数据集，不同数据集使用不同的顶层classifer，但是prefix continuous prompt是共享的
回归传统的CLS和token label classifier
主要是为了解决一些没有语义的标签的问题

// 待更

第四部分 LoRA: Low-Rank Adaptation of Large Language Models

4.1 什么是LoRA

如此文《LLaMA的解读与其微调：Alpaca-LoRA/Vicuna/BELLE/中文LLaMA/姜子牙/LLaMA 2》中的2.2.3节Alpaca-LoRA：通过PEFT库在消费级GPU上微调「基于LLaMA的Alpaca」所述，在神经网络模型中，模型参数通常以矩阵的形式表示。对于一个预训练好的模型，其参数矩阵已经包含了很多有用的信息。为了使模型适应特定任务，我们需要对这些参数进行微调

而当预训练比较大的模型时，微调模型的所有参数不太可行。以 GPT-3 175B 为例——部署微调模型的独的成本极其昂贵。为此，微软的研究者们于2021年通过论文《LoRA: Low-Rank Adaptation of Large Language Models》提出了低秩适应LoRA

它冻结了预训练的模型权重，并将可训练的秩分解矩阵注入到 Transformer 架构的每一层中，大大减少了下游任务的可训练参数的数量
We propose Low-Rank Adaptation, or LoRA, which freezes the pre-trained model weights and injects trainable rank decomposition matrices into each layer of the Transformer architecture, greatly reducing the number of trainable parameters for downstream tasks.
与使用 Adam 微调的 GPT-3 175B 相比，LoRA 可以将可训练参数数量减少 10,000 倍，GPU 内存需求减少 3 倍
Compared to GPT-3 175B fine-tuned with Adam, LoRA can reduce the number of trainable parameters by 10,000 times and the GPU memory requirement by 3 times

简言之，LoRA的核心思想是用一种低秩的方式来调整这些参数矩阵。在数学上，低秩意味着一个矩阵可以用两个较小的矩阵相乘来近似，可知

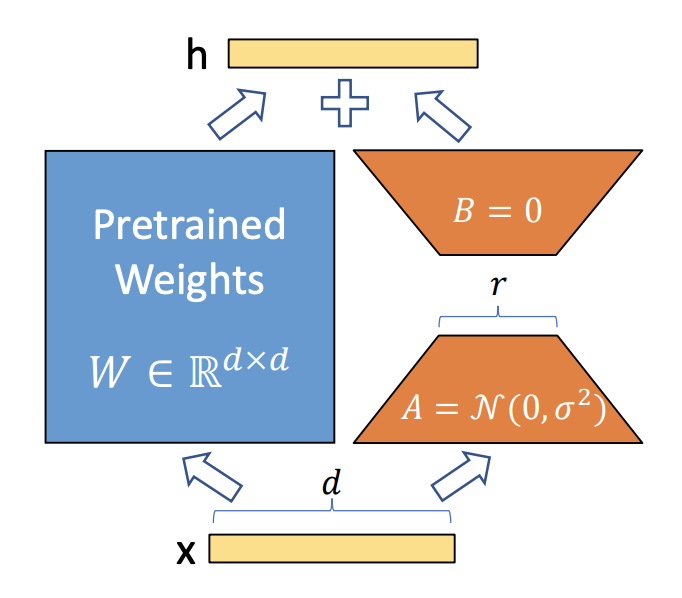
选择目标层：首先，在预训练神经网络模型中选择要应用LoRA的目标层。这些层通常是与特定任务相关的，如自注意力机制中的查询Q和键K矩阵

值得注意的是，原则上，我们可以将LoRA应用于神经网络中权矩阵的任何子集，以减少可训练参数的数量。在Transformer体系结构中，自关注模块(Wq、Wk、Wv、Wo)中有四个权重矩阵，MLP模块中有两个权重矩阵。我们将Wq(或Wk，Wv)作为维度 $d_{model} \times d_{model}$ 的单个矩阵，尽管输出维度通常被切分为注意力头
In principle, we can apply LoRA to any subset of weight matrices in a neural network to reduce thenumber of trainable parameters. In the Transformer architecture, there are four weight matrices inthe self-attention module (Wq, Wk, Wv, Wo) and two in the MLP module. We treat Wq (or Wk, Wv)as a single matrix of dimension $d_{model} \times d_{model}$ , even though the output dimension is usually slicedinto attention heads
不过，为了简单和参数效率，我们将研究限制为仅适应下游任务的注意力权重，并冻结MLP模块(因此它们不接受下游任务的训练)
We limit our study to only adapting the attention weights for downstreamtasks and freeze the MLP modules (so they are not trained in downstream tasks) both for simplicityand parameter-efficiency
初始化映射矩阵和逆映射矩阵：为目标层创建两个较小的矩阵 $A$ 和 $B$ ，然后进行变换
$\rightarrow$ $A$ 是映射矩阵(一般用随机高斯分布初始化，当然实际代码实现时，比如微软的deepspeed chat在用到LoRA时，一开始通过0矩阵占位，然后调用搭配ReLU激活函数的kaiming均匀分布初始化，虽与LoRA原始定义所用的高斯分布初始化不同，但此两种初始化方式都可以工作，更多介绍见下面deepspeed chat的代码 )，维度上是降维
$\rightarrow$ $B$ 是逆映射矩阵(用0矩阵初始化)，维度上是升维
之后做参数变换：将目标层的原始参数矩阵W通过映射矩阵A和逆映射矩阵B进行变换，计算公式为： $W' = W + A * B$ ，这里W'是变换后的参数矩阵

其中，矩阵的大小由LoRA的秩(rank)和alpha值确定
即实际实现时，会对 $AB$ 的结果通过 $\frac{\alpha }{r}$ 进行缩放 (在下节你会看到，self.lora_scaling = lora_scaling / lora_dim，其中可默认 lora_scaling=1，而lora_dim 可人为设定，比如128维 )
微调模型：使用新的参数矩阵 $W'$ 替换目标层的原始参数矩阵 $W$ ，然后在特定任务的训练数据上对模型进行微调
梯度更新：在微调过程中，计算损失函数关于映射矩阵A和逆映射矩阵B的梯度，并使用优化算法(如Adam、SGD等)对A和B进行更新
注意，在更新过程中，原始参数矩阵W保持不变，说白了，训练的时候固定原始PLM的参数，只训练降维矩阵A与升维矩阵B
(W is frozen and does not receive gradient updates, while A and B contain trainableparameters )
重复更新：在训练的每个批次中，重复步骤3-5，直到达到预定的训练轮次(epoch)或满足收敛条件

且当需要切换到另一个下游任务时，可以通过减去B A然后添加不同的B' A'来恢复W，这是一个内存开销很小的快速操作(When we need to switch to another downstream task, we can recover W0 by subtracting BA andthen adding a different B0A0, a quick operation with very little memory overhead )

总之，LoRA的详细步骤包括选择目标层、初始化映射矩阵和逆映射矩阵、进行参数变换和模型微调。在微调过程中，模型会通过更新映射矩阵U和逆映射矩阵V来学习特定任务的知识，从而提高模型在该任务上的性能

4.2 微软DeepSpeed-Chat中对LoRA微调的实现

继续说一下，这个LoRA的应用还是挺广的，比如后续微软推出的DeepSpeed-Chat便用了这个方法

DeepSpeed-Chat的实现中，当设置LoRA的低秩维度lora_dim（如lora_dim=128）时，即认为启用了LoRA训练，则将原始模型中名称含有“deoder.layers.”且为线性层修改为LoRA层，具体操作为：

将原始结构的weight参数冻结；
新引入了2个线性层lora_right_weight和lora_left_weight (分别对应上图中的降维矩阵A、升维矩阵B )，可实现先降维至lora_dim再升维回原维度；
LoRA层主要实现了两分支通路，一条分支为已被冻结weight参数的原始结构、另一条分支为新引入的降维再升维线性层组

核心代码如下(小部分取自training/step1_supervised_finetuning/main.py，大部分取自training/utils/module/lora.py)


# applications/DeepSpeed-Chat/training/step1_supervised_finetuning/main.py
# 判断是否启用LoRA模式
if args.lora_dim > 0:
"""
如果启用，则对名称中含有“decoder.layers.”且为线性层的结构部分引入LoRA旁路（实现先降维后升维的2个线性层），
这类结构基本都是attention、信息交互用的inner线性层，
这类结构的Weight参数将被冻结，转而优化LoRA旁路的参数。
"""
    args.lora_module_name = "decoder.layers."
    model = convert_linear_layer_to_lora(model, args.lora_module_name,
                                         args.lora_dim)
 
# applications/DeepSpeed-Chat/training/utils/module/lora.py
def convert_linear_layer_to_lora(model,
                                 part_module_name,
                                 lora_dim=0,
                                 lora_scaling=1,
                                 lora_droppout=0):
    """
	将名称中带有"decoder.layers."的线性层转换为lora层
	"""
	"""取出模型中参数名含有decoder.layers.的线性层"""
    repalce_name = []
    for name, module in model.named_modules():
        if isinstance(module, nn.Linear) and part_module_name in name:
            repalce_name.append(name)
 
    for name in repalce_name:
    	"""recursive_getattr实现了从model中根据属性名取出对应原始结构"""
        module = recursive_getattr(model, name)
 
        """纳入原始结构的参数，实例化lora层"""
        tmp = LinearLayer_LoRA(
            module.weight, lora_dim, lora_scaling, lora_droppout,
            module.bias).to(module.weight.device).to(module.weight.dtype)
 
        """recursive_getattr实现了将model对应属性的结构换成lora层实例"""
        recursive_setattr(model, name, tmp)
    return model
    
# applications/DeepSpeed-Chat/training/utils/module/lora.py
class LinearLayer_LoRA(nn.Module):
	"""具体的lora层"""
	def __init__(...):
		...
		"""此处的weight和bias即为原始结构中的参数"""
		self.weight = weight
		self.bias = bias
		···
 
		"""冻结weight部分的参数"""
		self.weight.requires_grad = False
		···
		self.lora_right_weight = nn.Parameter(torch.zeros(columns, lora_dim))
	    self.lora_left_weight = nn.Parameter(torch.zeros(lora_dim, rows))
        ...
 
	    """初始化LoRA线性层的参数"""
	    self.reset_parameters()
 
    # 调用reset_parameters(self)做初始化
    def reset_parameters(self):
    	# 降维矩阵与LoRA原始定义所用的(0,\sigma^2)正态分布初始化不同，而是使用的kaiming均匀分布初始化
    	# kaiming服从均匀分布U(-\sqrt{1/in_feature}, +\sqrt{1/in_feature})
        # f_i是矩阵的输入维度，就是nn.Linear(in_features, out_features)中的in_features
        # 对应上面代码中的columns，而这个columns相当于基座模型的hidden_size
        nn.init.kaiming_uniform_(self.lora_right_weight, a=math.sqrt(5))
 
        # 升维矩阵使用全0初始化
        nn.init.zeros_(self.lora_left_weight)
 
    def forward(self, input):
    	"""LoRA的正向传播"""
    	···
    	else:
            # F.linear(input, self.weight, self.bias)是使用给定的权重self.weight和偏差self.bias对输入数据input进行线性变换
            # 这个操作等价于input @ self.weight.t() + self.bias，其中@表示矩阵乘法，.t()表示矩阵转置
	    	return F.linear(input, self.weight, self.bias) 
                    # 1，self.lora_dropout(input)对输入进行了随机的dropout操作，这是一种正则化手段
                    # 2，对结果进行两次线性变换，一次是@ self.lora_right_weight，然后是@ self.lora_left_weight
                    # 3，乘法部分* self.lora_scaling是对加号后面部分的结果进行缩放
	    			+ (self.lora_dropout(input) @ self.lora_right_weight @ self.lora_left_weight) * self.lora_scaling

再额外分析下这段代码的最后部分


# applications/DeepSpeed-Chat/training/utils/module/lora.py
class LinearLayer_LoRA(nn.Module):
	"""具体的lora层"""
	···
    def forward(self, input):
    	"""LoRA的正向传播"""
    	···
    	else:
	    	return F.linear(
	                input, self.weight,
	                self.bias) + (self.lora_dropout(input) @ self.lora_right_weight
	                              @ self.lora_left_weight) * self.lora_scaling

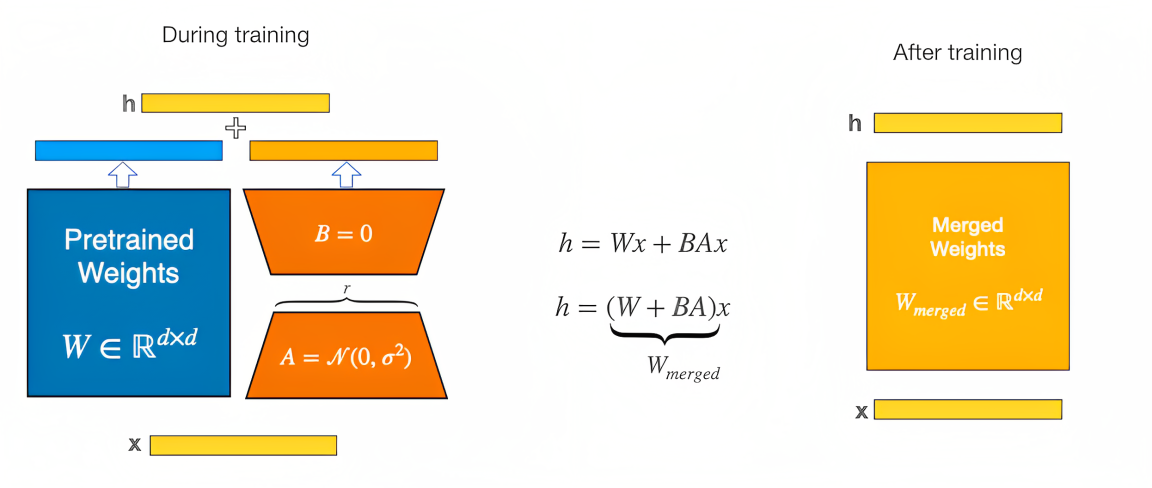
常规部分的正向传播由transformers所定义，而LoRA部分的正向传播则由LinearLayer_LoRA(nn.Module)的forward()所定义，即“LoRA层的两条分支结果进行加和”，如下图所示『图源：LoRA，相当于在训练期间，较小的权重矩阵(下图中的A和B)是分开的，但一旦训练完成，权重可以合并到一个新权重矩阵中 』

在代码中体现为

F.linear(input, self.weight, self.bias) + (self.lora_dropout(input) @ self.lora_right_weight @ self.lora_left_weight) * self.lora_scaling

加号左侧为原结构支路，加号右侧为新增支路，self.lora_right_weight 和self.lora_left_weight 分别为两个新引入线性层的参数

4.3 Huggingface上PEFT库对LoRA、Prefix Tuning、P-Tuning的封装

而Huggingface公司推出的PEFT(Parameter-Efficient Fine-Tuning，即高效参数微调之意) 库也封装了LoRA这个方法，PEFT库可以使预训练语言模型高效适应各种下游任务，而无需微调模型的所有参数，即仅微调少量(额外)模型参数，从而大大降低了计算和存储成本

Model	Full Finetuning	PEFT-LoRA PyTorch	PEFT-LoRA DeepSpeed with CPU Offloading
bigscience/T0_3B (3B params)	47.14GB GPU / 2.96GB CPU	14.4GB GPU / 2.96GB CPU	9.8GB GPU / 17.8GB CPU
bigscience/mt0-xxl (12B params)	OOM GPU	56GB GPU / 3GB CPU	22GB GPU / 52GB CPU
bigscience/bloomz-7b1 (7B params)	OOM GPU	32GB GPU / 3.8GB CPU	18.1GB GPU / 35GB CPU

且PEFT库 (peft/src/peft/peft_model.py at main · huggingface/peft · GitHub)支持以下流行的方法

LoRA，PEFT对LoRA的实现封装见：peft/src/peft/tuners/lora.py at main · huggingface/peft · GitHub，比如对权重的合并代码 (和上面DSC对LoRA权重合并的实现，在本质上是一致的)


def merge(self): 
    # 检查当前激活的适配器是否在lora_A的键中，如果不在则终止函数
    if self.active_adapter not in self.lora_A.keys():  
        return  
 
    if self.merged:  
        warnings.warn("Already merged. Nothing to do.")
        return  
 
    # 如果激活适配器的r值大于0，表示有可以合并的权重
    if self.r[self.active_adapter] > 0: 
        # 在当前的权重上加上计算得到的新权重
        self.weight.data += (  
            # 转置运算
            transpose(  
                # 通过矩阵乘法计算新的权重
                self.lora_B[self.active_adapter].weight @ self.lora_A[self.active_adapter].weight, 
 
                # 这是转置运算的维度参数
                self.fan_in_fan_out,  
            )
 
            # 然后将计算得到的权重乘以对应的缩放因子
            * self.scaling[self.active_adapter]  
        )
        self.merged = True

Prefix Tuning: Prefix-Tuning: Optimizing Continuous Prompts for Generation, P-Tuning v2: Prompt Tuning Can Be Comparable to Fine-tuning Universally Across Scales and Tasks
P-Tuning: GPT Understands, Too
Prompt Tuning: The Power of Scale for Parameter-Efficient Prompt Tuning

第五部分 QLoRA：结合模型量化Quant 和 LoRA 参数微调

QLoRA于今23年5月份通过此篇论文《QLORA: Efficient Finetuning of Quantized LLMs》被提出，本质是对LoRA的改进，相比LoRA进一步降低显存消耗，话怎讲？

因为LoRa为LLM的每一层添加了少量的可训练参数(适配器)，并冻结了所有原始参数。这样对于微调，只需要更新适配器权重，这可以显著减少内存占用
而QLoRa更进一步，引入了4位量化、双量化和利用nVidia统一内存进行分页(细节下文详解)
所有这些步骤都大大减少了微调所需的内存，同时性能几乎与标准微调相当

下图总结了不同的微调方法及其内存需求，其中的QLoRA通过将模型量化到4位精度并使用分页优化器管理内存峰值来改进LoRA

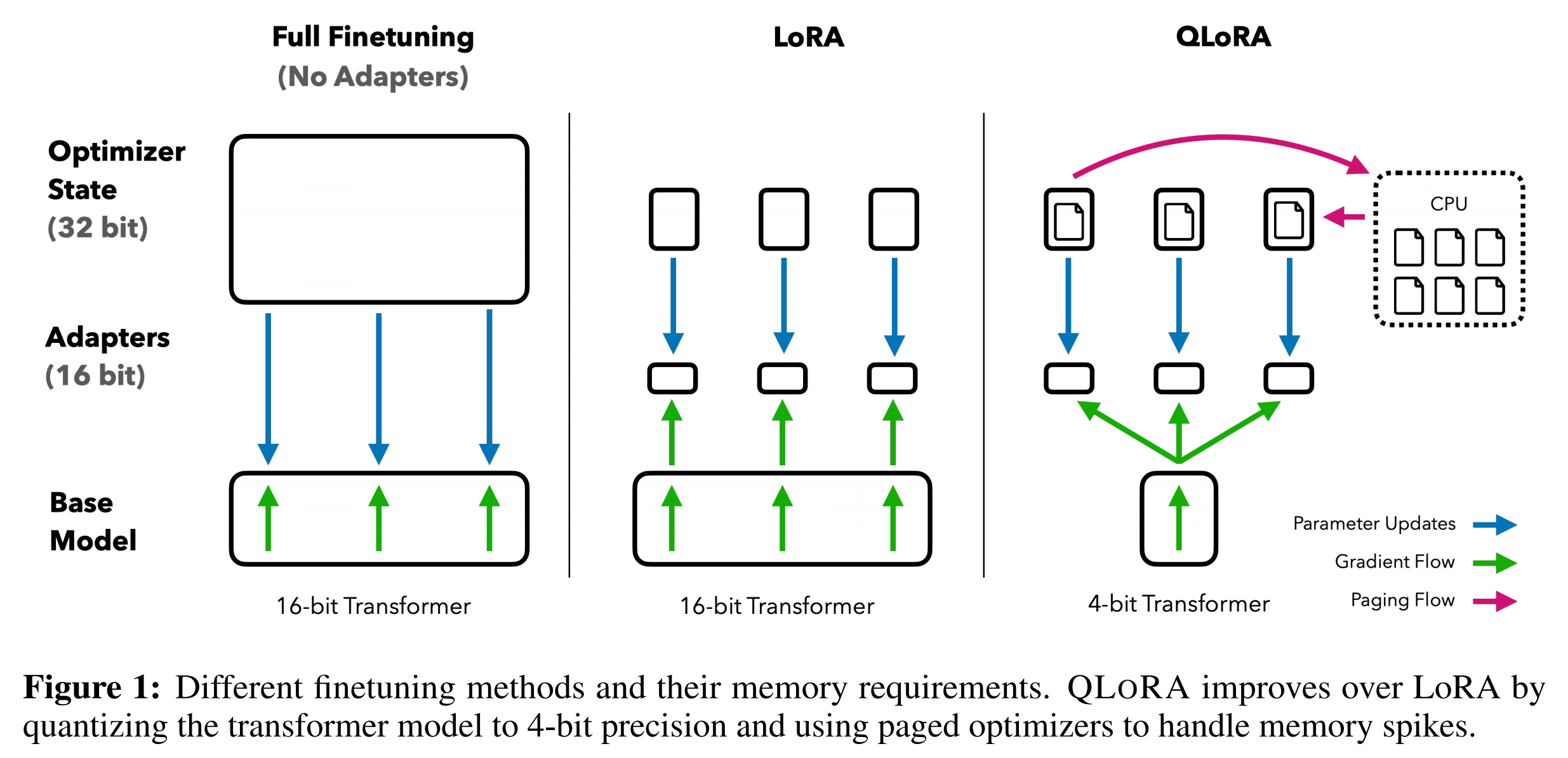
可能论文中的这个图还不够一目了然，那可以对比下图

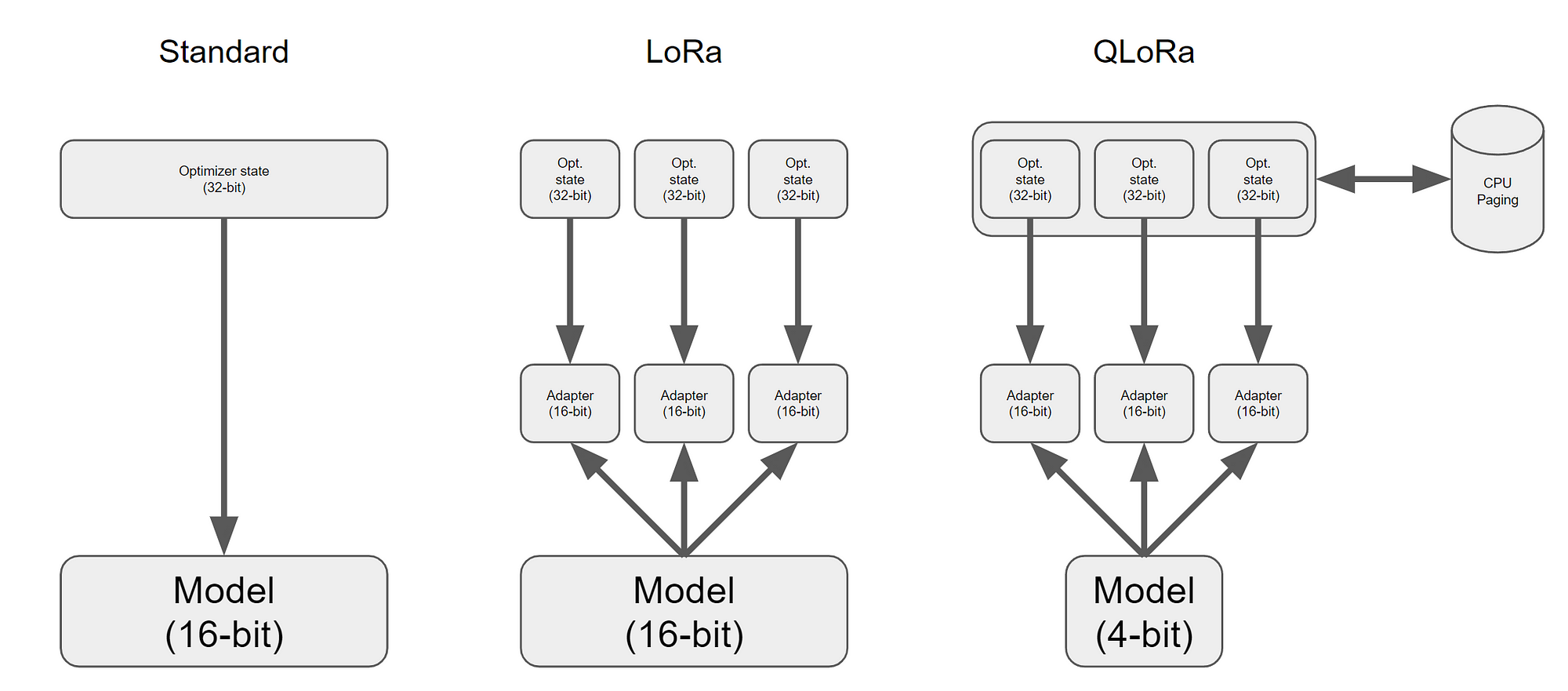
Comparison between standard, LoRa, and QLoRa for fine-tuning an LLM such as GPT.

5.1 模型量化到底是怎么一回事？

5.1.1 什么是模型量化及其好处

上文提到，QLoRa中用到了4位NormalFloat量化和双量化，那到底什么是量化呢？

第一，简单来讲，模型量化是将浮点数值转化为定点数值，同时尽可能减少计算精度损失的方法
具体而言，模型量化是一种压缩网络参数的方式，它将神经网络的参数(weight)、特征图(activation)等原本用浮点表示的量值换用定点(整型)表示，在计算过程中，再将定点数据反量化回浮点数据，得到结果，如下图所示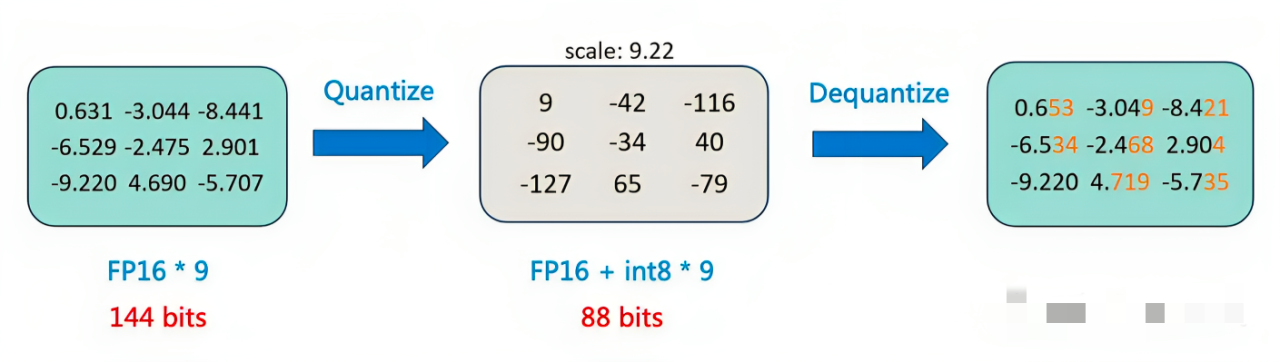
第二，综合而言，我们可以对模型参数(weight)、激活值(activation)或者梯度(gradient)做量化。通常而言，模型的参数分布较为稳定，因此对参数 weight 做量化较为容易(比如，QLoRA便是对weight做量化)
至于模型的激活值往往存在异常值，直接对其做量化，会降低有效的量化格点数，导致精度损失严重，因此，激活值的量化需要更复杂的处理方法(如SmoothQuant)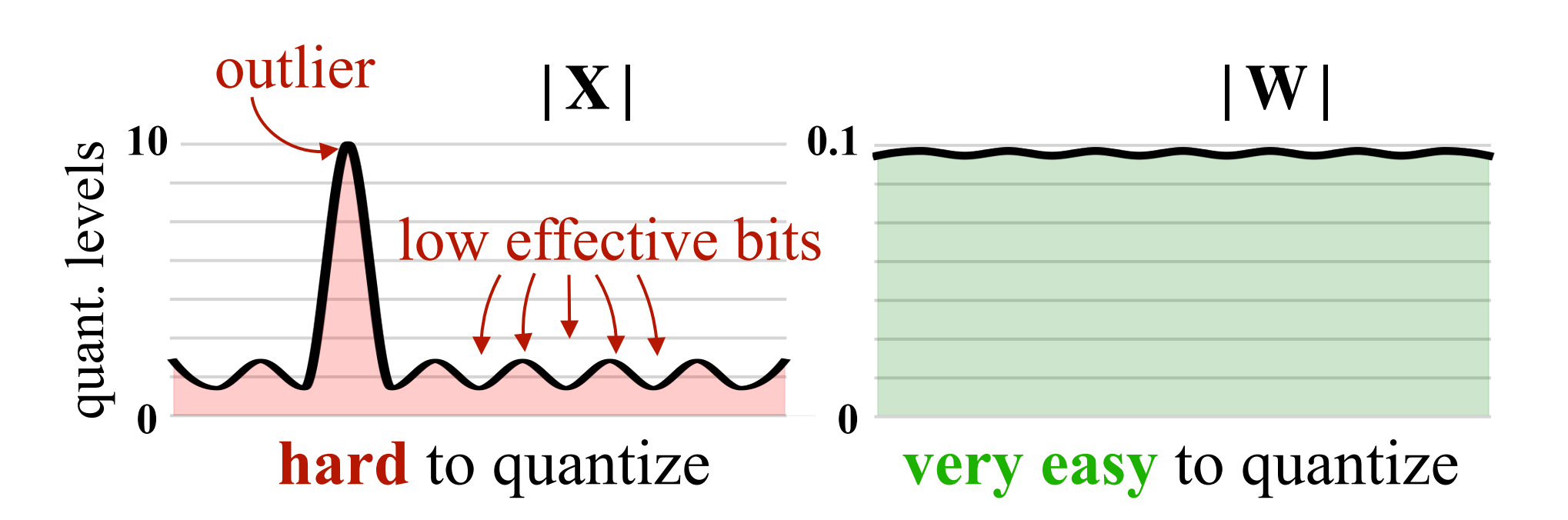
第三，通常可以将模型量化为 int4、int8 等整型数据格式
在大模型方向上，模型的计算一般采用 16-bit 精度(FP16、BF16等)，所以通常我们需要将 int4/int8 转化为 FP16/BF16，然后再进行计算
如果我们自己实现了 int4/int8 的 cuda kernel，或者 GPU 有 int4/int8 的矩阵运算支持，也可以在低精度下直接运算
除此之外，NVIDIA Hopper 框架支持了 FP8 的低精度运算，可以在硬件层面上实现模型的高效训练和推理

模型量化实现建立在深度网络对噪声具有一定的容忍性上，模型量化相当于对深度网络增加了一定的噪声(量化误差)，如果量化位数合适，模型量化基本不会造成较大的精度损失，但模型量化的好处多多

简言之，模型量化既能减少资源消耗，也能提高运行速度，使大规模推理服务的性能提升

展开讲，模型量化的好处主要有：

可以减少内存和显存占用，给模型瘦身，降低大模型的使用门槛和资源消耗；
如果将16B参数的 MOSS 模型做int4量化，加载模型所需显存就可以从 32GB 降低到10GB，使得 MOSS 能在普通的消费级显卡上跑推理
能够提高运行速度，这可以从两方面理解：
i) 在适配低精度的硬件下，量化模型的运算能直接用 int8 GEMM kernel 计算
ii) 量化减少了单位数据的 bit 数，因而可以减少计算过程中的 IO 通信量
由于以上两点，做模型推理时，可以增大 batch size，同时也能加快计算速度，因此规模化的模型推理就能既快速又高效
可以参考 vLLM 大规模推理服务的实践：vLLM 提出的 PagedAttention 能够减少显存碎片和实现显存共享，既使得一次推理的 batch size 增大，也同时实现了高效的并行推理。

5.1.2 量化方法有哪些分类？

根据量化方案的不同，可以分为量化感知训练(QAT)和后训练量化(PTQ)

QAT(Quant-Aware Training)也可以称为在线量化(On Quantization)。它需要利用额外的训练数据，在量化的同时结合反向传播对模型权重进行调整，意在确保量化模型的精度不掉点
PTQ (Post Training Quantization)也可以称为离线量化(Off Quantization)。它是在已训练的模型上，使用少量或不使用额外数据，对模型量化过程进行校准，可能伴有模型权重的缩放。其中：
训练后动态量化(PostDynamic Quantization)，不使用校准数据集，直接对每一层 layer 通过量化公式进行转换，QLoRA 就是采用这种方法
训练后校正量化(Post Calibration Quantization)，需要输入有代表性的数据集，根据模型每一层 layer 的输入输出调整量化权重，GPTQ 就是采用这种方法。

Pytorch 对上述三种量化方式，都提供了相应的 API

根据量化公式的不同，可以分为线性量化和非线性量化，也可以分为对称量化和非对称量化

在线性量化下，浮点数 $R$ 与定点数 $Q$ 之间的转换公式如下：

$Q=\frac{R}{S}+Z$

变换一下，则可得：

$R=(Q-Z) * S$

R 表示量化前的浮点数，Q 表示量化后的定点数，S(Scale)表示缩放因子的数值，Z(Zero)表示零点的数值

一般的文章讲到上述程度便不错了，但July我还是得再深入解释下，其实，将模型从FP32转换为INT8用下面这个公式来表示可能更好理解些，即

$x_{\text {quant }}=\operatorname{round}\left(\frac{x_{\text {float }}}{s}\right)+z$

其中， $x_{\text {quant }}$ 是量化后的结果(整数形式)， $x_{\text {float }}$ 是原始的浮点数值， $s$ 是量化尺度(可理解为一个缩放因子)， $z$ 是量化零点(可以理解为一个位移量)，至于公式中的 $round$ 函数表示对数据进行四舍五入

相当于先将原始的浮点数值 $x_{\text {float }}$ 除以量化尺度 $s$ ，然后对结果进行四舍五入，最后加上量化零点 $z$ 。这样就完成了从浮点数到整数的量化过程，下文会有具体的计算例子

对称量化中(如下图左侧所示)，量化前后的 0 点是对齐的，因此不需要记录零点。它适合对分布良好且均值为 0 的参数进行量化，因此对称量化常用于对 weight 量化
非对称量化中(如下图右侧所示)，量化前后 0 点不对齐，需要额外记录一个 offset，也就是零点。非对称量化常用于对 activation 做量化

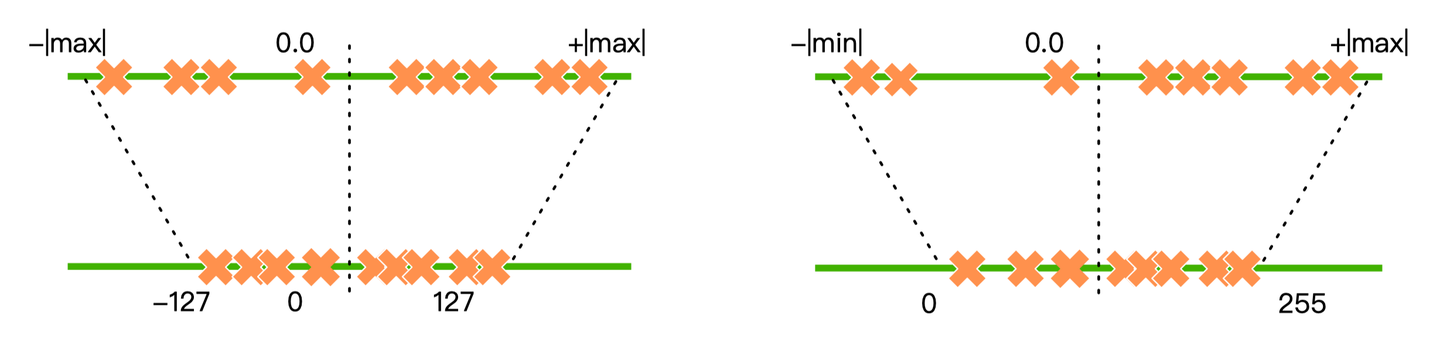
因QLoRA 和 GPTQ 都是对 weight 做量化，因此均采用对称量化的方法

5.1.3 全网最详细的模型量化实现示例

对称量化中，零点 Z = 0，一般不记录，我们只需要关心如何求解 Scale，怎么求解呢？

由于 weight 几乎不存在异常值，因此我们可以直接取 Scale 为一个 layer 或 block 内所有参数的最大绝对值，于是所有的参数都在 [-1, 1] 的区间内
随后，这些参数将找到最近的量化格点，并转化成定点数

举个例子，比如下图展示的是量化到 int8，首先把所有数值Scale它们中的最大绝对值9.22「相当于所有数值除以9.22，使得所有的参数都在 [-1, 1] 的区间内」，然后做Round to Grid，具体分两步：先乘以 127「相当于2^(8-1)-1」，后 round 到最近的整数

考虑到如果是一位中学生阅读此文，可能会因为没有相关的背景知识则造成阅读卡壳，故一为扫清任何理解上的障碍，二为坚持July行文必须通俗易懂，特此解释以下几点

首先，什么是INT 8呢
int8 是一个 8 位的有符号整数。这意味着它由 8 个二进制位组成，其中最高位(称为最高有效位，MSB)用作符号位
当符号位为 0 时，整数为正；当符号位为 1 时，整数为负

现在，考虑没有符号位的剩余 7 位：
$\rightarrow$ 它们的最大正数值是(回忆下二进制到十进制的转换) $1111111_2 = 127_{10}$
$\rightarrow$ 它们的最大负数值(在二进制补码表示中)是 $10000000_2$ ，这在十进制中等于 -128，为什么是这样？在补码表示法中，为了得到一个数的负表示，你需要取其正值的二进制补码
举个例子，对于 1，它的二进制表示是 $0000001_2$ 。其补码是取反所有位，然后加 1，得到 $1111111_2$ ，即：-1

当你用这种方式继续到 $10000000_2$ ，即得到 -128，这是 8 位二进制数可以表示的最小整数
因此，由于这 8 位的约束和补码的表示，int8 的范围是 -128 到 127
Round to Grid：这是一个通用术语，意思是将一个值四舍五入到某个“网格”上。在这个上下文中，它意味着我们想将浮点数四舍五入到最近的整数值
先乘以 127：这是一个缩放步骤。乘以127是为了使得1.0(或者接近于1.0的值)映射到int8的最大值127
然后 round 到最近的整数：这意味着在乘以127之后，我们将结果四舍五入到最近的整数
范围限制：最后，我们将a限制在-90和79之间。如果a小于-90，我们就将其设置为-90；如果a大于79，我们就将其设置为79。得到的结果b就是我们的输出值
计算公式：b = min(max(a, -90), 79)

所以，简而言之，上面那个例子描述了如何通过缩放和四舍五入来将浮点数转换为int8整数

进一步，为考虑其他更多情况，需要引入一种新的量化策略：Block-wise quantization(块级量化)

通常情况，为了避免异常值(outlier)的影响，我们会将输入tensor(通常是神经网络的权重或激活值)分割成多个块(block)，然后每个块(block)单独做量化，有单独的缩放因子scale和零点zero
这种块级量化的好处是可以为不同的数据块选择不同的量化策略。例如，某些块可以用更高的位宽量化，而其他块则可以用更低的位宽
当然，尽管块级量化可以提供更好的精度，但由于每个块都有自己的量化参数，这可能会增加计算和存储的开销

总之，块级量化最终能使量化的精度损失减少(见下图橙色的误差部分)

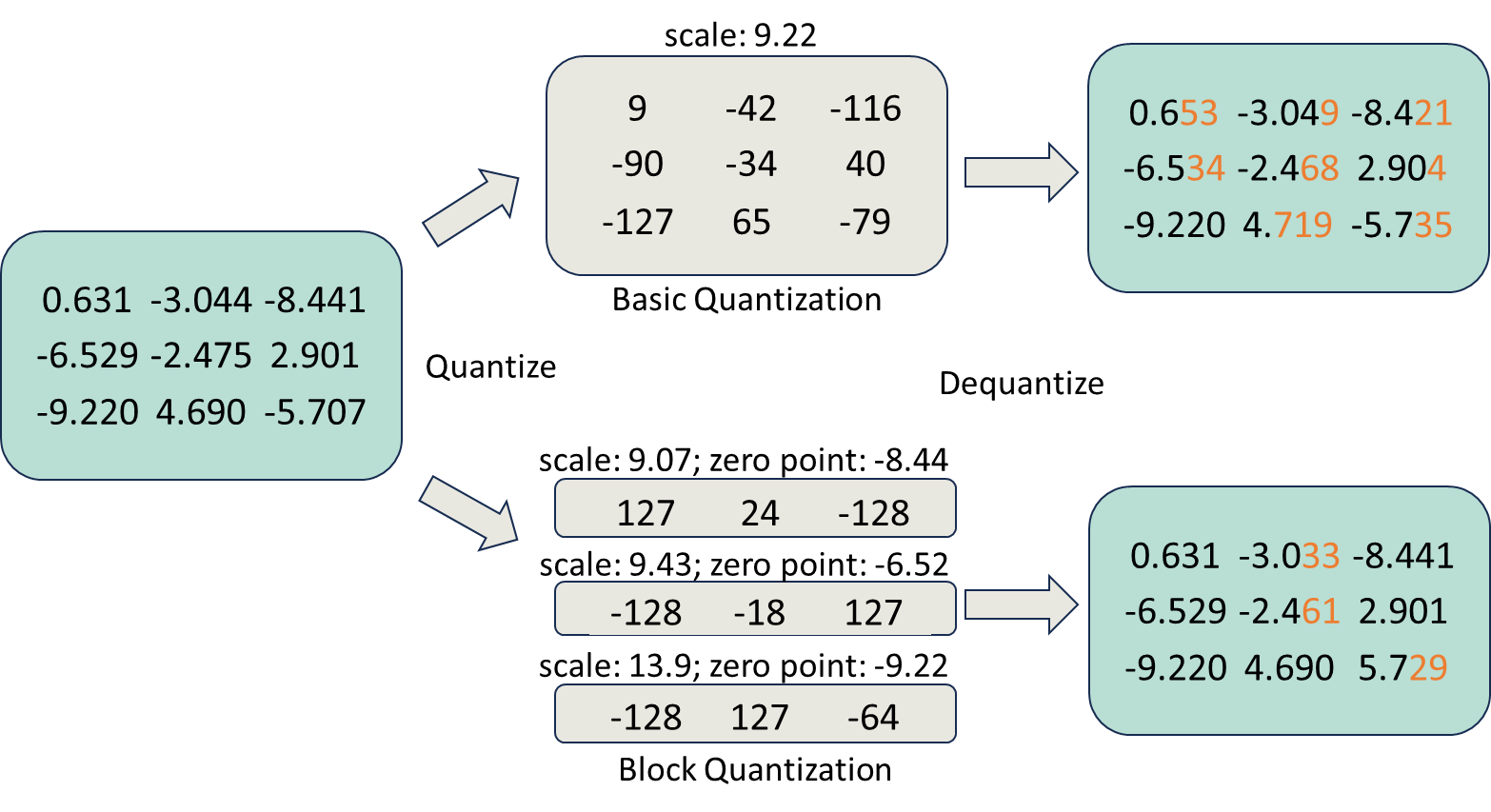
为保持July行文通俗易懂的特点起见，还是得再补充说明下

图的上半部分是先做了基本量化，然后再做反量化
基本量化的操作如上上图所示
$\rightarrow$ 缩放：我们首先将x除以最大绝对值9.22，得到一个新的值y。这个步骤可以确保y在-1和1之间
计算公式：y = x / 9.22
$\rightarrow$ 乘以比例尺：然后，我们将y乘以127（相当于2^(8-1)-1），得到一个新的值z。这个步骤可以确保z在-127和127之间
计算公式：z = y * 127
$\rightarrow$ 四舍五入：接下来，我们将z四舍五入到最近的整数，得到一个新的值a
计算公式：a = round(z)
$\rightarrow$ 范围限制：最后，我们将a限制在-90和79之间。如果a小于-90，我们就将其设置为-90；如果a大于79，我们就将其设置为79。得到的结果b就是我们的输出值
计算公式：b = min(max(a, -90), 79)

再之后，再做反量化到浮点数
$\rightarrow$ 范围反转：我们首先将量化后的值从-90和79的范围反转回-127和127的范围。如果值是-90，我们就将其设置为-127；如果值是79，我们就将其设置为127
$\rightarrow$ 除以比例尺：然后，我们将这个值除以127（相当于2^(8-1)-1），得到一个新的值
$\rightarrow$ 反缩放：最后，我们将这个新的值乘以最大绝对值9.22，得到原始的浮点数

最终可以通过对比最初的浮点数与最后的浮点数的差异，得出具体的误差(橙色部分表示误差)
图的下半部分是做块级量化
对于原始的浮点数，总共三行，每一行都可以采取不同的缩放因子scale和零点zero分别做量化，最后再做反量化

截止到23年十一之前，网上几乎所有文章可能说到上面那便戛然而止了，但到底是怎么一个具体的计算过程呢？打破砂锅问到底，在和我司杜老师讨论之后，咱们来逐一计算下吧

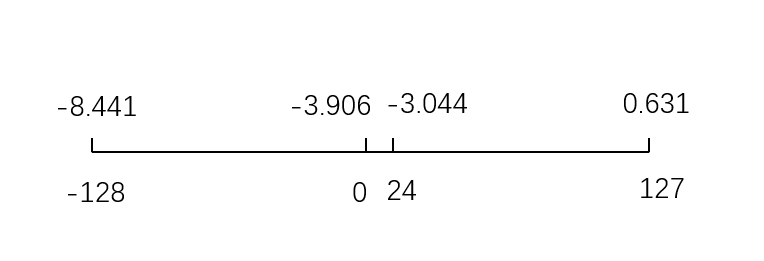
首先，如何做量化，使得
0.631 -3.044 -8.441
在scale: 9.07; zero point: -8.44下,得到
127 24 -128

简言之，通过等比计算把最小值-8.441到0.631这一共9.07的范围映射到-128到127范围内

首先，将实值乘以一个缩放因子，然后舍入到最近的整数；其次，将结果从[0, 255]映射到[-128, 127]范围
使用此策略，具体步骤如下：
量化：Q′ = round {[(real_value−zero_point)/scale] ×255}
映射到[-128, 127]：Q=Q′−128，即

其中
浮点数的最大值减去最小值则是实值范围定义为Realrange，即scale
INT8的量化范围Qrange=127−(−128)=255
故缩放因子最终为： $\frac{scale}{255}$
偏移量被定义为zero_point
最后减去128，是为了映射到[-128, 127]范围

故当给定：
scale=9.07
zero_point=−8.44
便可计算出每一个值
1) 对于 0.631:
Q′=round { [(0.631- -8.44)/9.07] × 255 }
Q′=round(255)=255
映射到[-128, 127]范围: Q=255−128=127
2) 对于 -3.044:
Q′=round{ [(−3.044- -8.44)/9.07] × 255 }
Q′=round(152.474)=152
映射到[-128, 127]范围: Q=152−128=24
3) 对于 -8.441:
Q′=round{ [(−8.441- -8.44)/9.07] × 255 }
Q′=round(0.0022×255)=0
映射到[-128, 127]范围: Q=0−128=−128
所以，使用这个稍微调整过的量化策略，我们得到了期望的量化结果：127, 24, -128
其次，如何做量化，使得
-6.529 -2.475 2.901
在scale: 9.43; zero point:-6.52下
得到 -128 -18 127

现在，依然使用下述公式进行量化
Q = round { [(real_value+zero_point)/scale]×255} - 128

1) 对于 -6.529:
Q=round{ [ (−6.529- -6.52)/9.43 ] × 255 } - 128
Q=round(0) - 128 = 0−128 = −128
2) 对于 -2.475:
Q=round{ [ (−2.475- -6.52)/9.43 ] × 255 } - 128
Q=round(109.5676) - 128 = 110 −128 = −18
3) 对于 2.901:
Q=round{ [ (2.901- -6.52)/9.43 ] × 255 }
Q=round(254.3243) - 128 = 254 −128 = 126
所以，最终的量化值是 -128, -18 和 126。我们发现第三个值有1的偏差，可能是由于四舍五入的结果造成的
最后，如何做量化，使得
-9.220 4.690 -5.707
在scale: 13.9; zero point:-9.22下，得到
-128 127 -64

原因很简单，还是依据如下计算公式
Q=round { [(real_value+zero_point)/scale] ×255}−128

1) 对于 -9.220:
Q=round{ [(9.220- -9.22)/13.9]×255}−128
Q=round(0×255)−128
Q=−128
2) 对于 4.690:
Q=round{ [(4.690- -9.22)/13.9]×255}−128
Q=round(1×255)−128
Q=127
3) 对于 -5.707:
Q=round{ [(−5.707- -9.22)/13.9]×255}−128
Q=round(0.253×255)−128
Q=round(64.515)−128
Q=−64

最后，模型量化需要关注哪些指标呢？事实上，模型量化可以看成模型的压缩/解压过程，也可以理解成模型加密/解密的过程

既然量化算法相当于一个压缩算法，自然我们需要关注：

压缩比，也就是说，一种量化方法能减少多少内存/显存占用？
原因在于当我们确定了量化精度(例如 int4)，确定了量化方法，以及需要量化模型的哪些 layer，其内存和显存占用就基本确定下来了
大部分情况下，我们都只去量化 nn.Linear 层，目前几乎所有量化策略都是这么做的，而且量化模型的显存占用较少，因此我们几乎不会去考虑怎么进一步减少量化模型的体积
压缩/解压缩的速度，这影响量化模型推理的速度，也是我们需要重点优化之处
原因在于我们着重于模型forward、backward计算过程的解压缩速度。由于这些计算基本都在 GPU 上进行，所以我们就需要去优化 GPU 的 op 了

5.2 QLoRA：4位NormalFloat量化/双量化/统一内存分页——进一步降低显存消耗

QLoRA 同时结合了模型量化 Quant 和 LoRA 参数微调两种方法，因此可以在单张48GB的 GPU 上对一个65B 的大模型做 finetune。QLoRA 的量化方法(由 bitsandbytes 库提供 backend)也是 Transformers 官方的模型量化实现。

运用 QLoRA 的微调方法训练的模型 Guanaco 在多项任务上表现强劲，截止2023.07.14，Guanaco-65B 模型在 Open LLM Leaderboard 排名第二(当然，排行榜的指标仅是一种参考。比如现在的 LeaderBoard 已经被 Llama 2 等一众模型超越了)，大幅超越了原始的 llama-65B

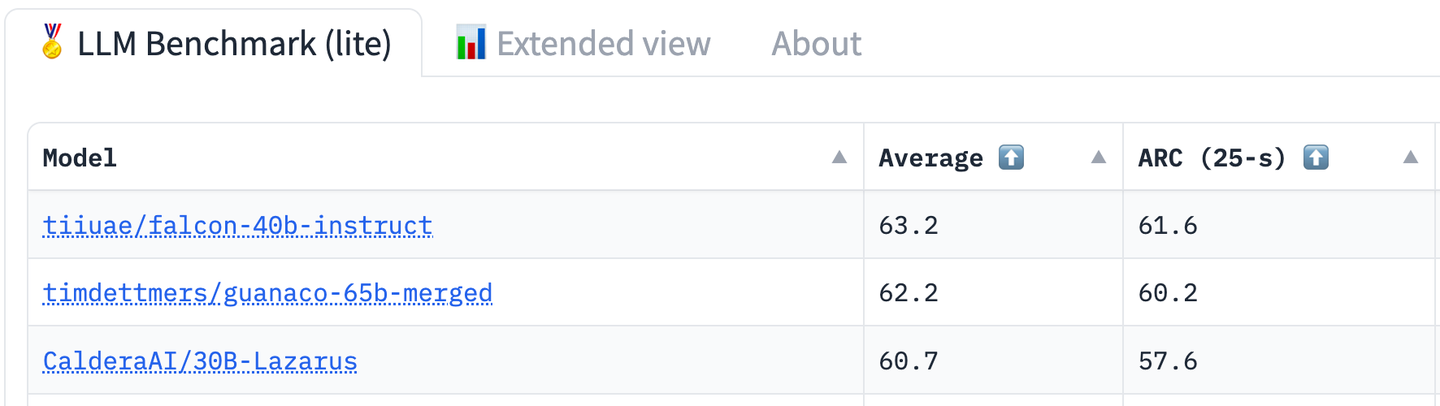
正因为 QLoRA 的高效训练方法和在下游任务的优秀表现，自公开 Guanaco 模型后，QLoRA 的这套方法也开始得到许多人的关注

QLoRA 针对模型权重(weight)做量化，采用的是对称量化算法，量化过程基本同上面讲述的方法一致，我们主要来看它的量化创新点，如之前所述，包括

4位NormalFloat量化：这是一种改进量化的方法。它确保每个量化仓中有相同数量的值
即采用新的 NF (NormalFloat)数据类型，它是对于正态分布权重而言信息理论上最优的数据类型，同时，NF 类型有助于缓解异常值的影响
双量化：QLoRa的作者将其定义如下：“对量化常量再次量化以节省额外内存的过程。”
即Double Quant，对于量化后的 scale 数据做进一步的量化

此外，除了以上量化部分的创新点之外，QLoRa还有统一内存分页：它依赖于NVIDIA统一内存管理，自动处理CPU和GPU之间的页到页传输，它可以保证GPU处理无错，特别是在GPU可能耗尽内存的情况下

5.2.1 NF4 数据类型：格点分布与数据分布一致

新的数据类型，可以看成新的格点分配策略。我们用一张图说明 int4 数据类型和 NF4 数据类型的区别

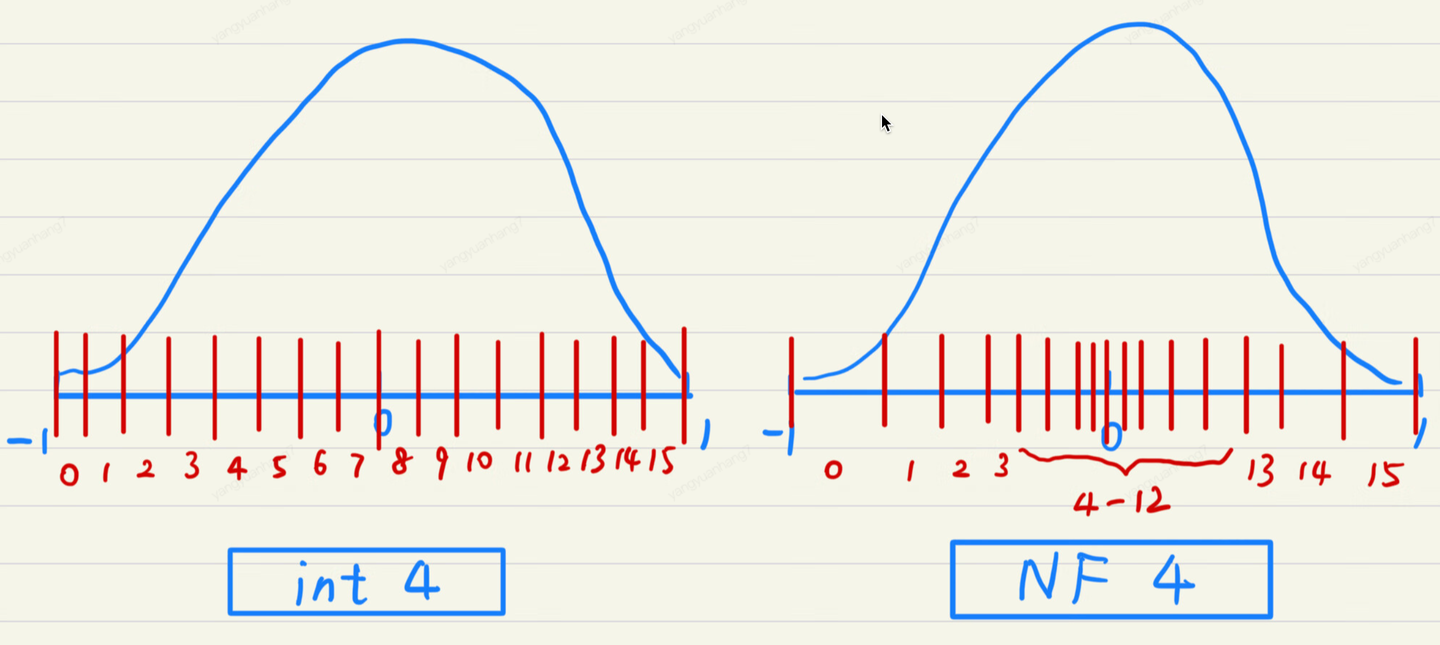
int4 的格点分布是均匀的，然而模型的权重通常服从均值为 0 的正态分布，因此格点的分布和数据的分布不一致。这会导致格点“供需”的不匹配，具体表现在
$\rightarrow$ 靠近 0 点的数据很多，但可用的格点数就相对较少，这样大量参数 round 的粒度较粗，会导致模型量化的精度受损；
$\rightarrow$ 远离 0 点的数据较少，而可用的格点数相对多，这部分的少量数据不需要太高的量化精度，因此部分格点就被浪费了
NF4 的格点按照正态分布的分位数截取，格点分布两端稀疏，中间密集，格点分布与数据分布一致。这样格点分配的效率就大大增加了，同时精度受损也不会太大

5.2.2 Double Quant：进一步降低显存消耗

QLoRA 将每 64 个参数为做一个 block，即 block_size = 64，每个 block 计算一个 Scale。由于量化后的 Scale 通常以 FP32 存储，在 block 数众多的情况下，Scale 占用的显存也不可忽视。因此，QLoRA 对 Scale 进一步量化成 FP8，取 Double Quant 的 block size = 256，因而进一步降低了显存消耗。

Double Quant 前，每个参数做量化会需要额外的 32/64 = 0.5 bits 显存；
Double Quant 后，每个参数做量化只需要额外的 8/64 + 32 / (64*256) = 0.127 bits 显存