智能营销模型-Uplift Model详解及Python使用

1. 背景概览

  在营销场景中，需要给不同的用户给出不同的营销动作，从而提升收益，如触达方式、广告投放或发放优惠券等。但往往我们无法同一时间观察实施不同动作下能带来的收益。Uplift Model是因果推断(Causal Inference)的一种应用，是根据A/B实验，对相似用户在不同营销动作下的增益，作为用户在不同营销动作下的增益，就如在不同的平行世界观察观察对不同营销动作的反应。

2. 方法介绍

  Uplift Model是需要基于以往AB实验的数据积累，将无营销动作（对照组）和有营销动作（实验组）构建模型，如下图所示。其中，在AB实验时实验组和对照组用户同分布。目前，Ulift Model的库CausalML、EconML和pylift等，本文后续Uplift Model使用均CausalML。后续主要介绍Uplift Model中的T-Learner、S-Learner、X-Learner和Causal Tree，除了这几种方法之外，还有R-Learner，NN中的TARNet、SITE和DragonNet等等

2.1 T-Learner

论文地址：https://arxiv.org/pdf/1706.03461.pdf
  T-Learner （Two Model）是将对照组和实验组分开建模，然后实验组模型与对照组模型响应概率的差即为提升值。以下是单Treatment场景的具体流程：

  步骤1: 使用对照组数据X和对应标签Y，训练模型
$${\mu }_0(x)=\mathbb{E}[Y(0)|X=x]$$
  步骤2: 使用实验组数据X和对应标签Y，训练模型
$${\mu }_1(x)=\mathbb{E}[Y(1)|X=x]$$
  步骤3: 计算样本x的动作带来的Uplift Score
$${\hat{\tau }}_T={\hat{\mu }}_1(x)-{\hat{\mu }}_0(x)$$

  在多实验场景中，如优惠券金额有多种，是将不同的实验组模型与对照组模型做差，得到不同动作下的uplift socre，然后，在根据不同约束从中选择最合适的动作。
  T-Learner方法具简单直观，但同时模型对样本利用不充分，对照组和实验组模型无法利用对方样本，且双模型存在累积误差，对数据不平衡响应较大

T-Learner Python使用

from xgboost.sklearn import XGBClassifier
from causalml.inference.meta import BaseTClassifier
from causalml.dataset import make_uplift_classification
from sklearn.model_selection import train_test_split
df, x_names = make_uplift_classification(treatment_name=['control', 'treatment'])
df_train, df_test = train_test_split(df, test_size=0.2, random_state=111)
base_model = XGBClassifier()
clf = BaseTClassifier(learner=base_model,control_name='control')
clf.fit(df_train[x_names].values,
                 treatment=df_train['treatment_group_key'].values,
                 y=df_train['conversion'].values)
y_pred = clf.predict(df_test[x_names].values)
1
2
3
4
5
6
7
8
9
10
11
12

2.2 S-Learner

论文地址：https://arxiv.org/pdf/1706.03461.pdf
  S-Learner是指单一模型，把对照组和实验组放在一起建模，把营销动作作为一个特征（如将对照组），特征加入训练特征，如下图所示。在预测时，改变不同的W值计算相应率，从而与对照组相减得到uplift score。

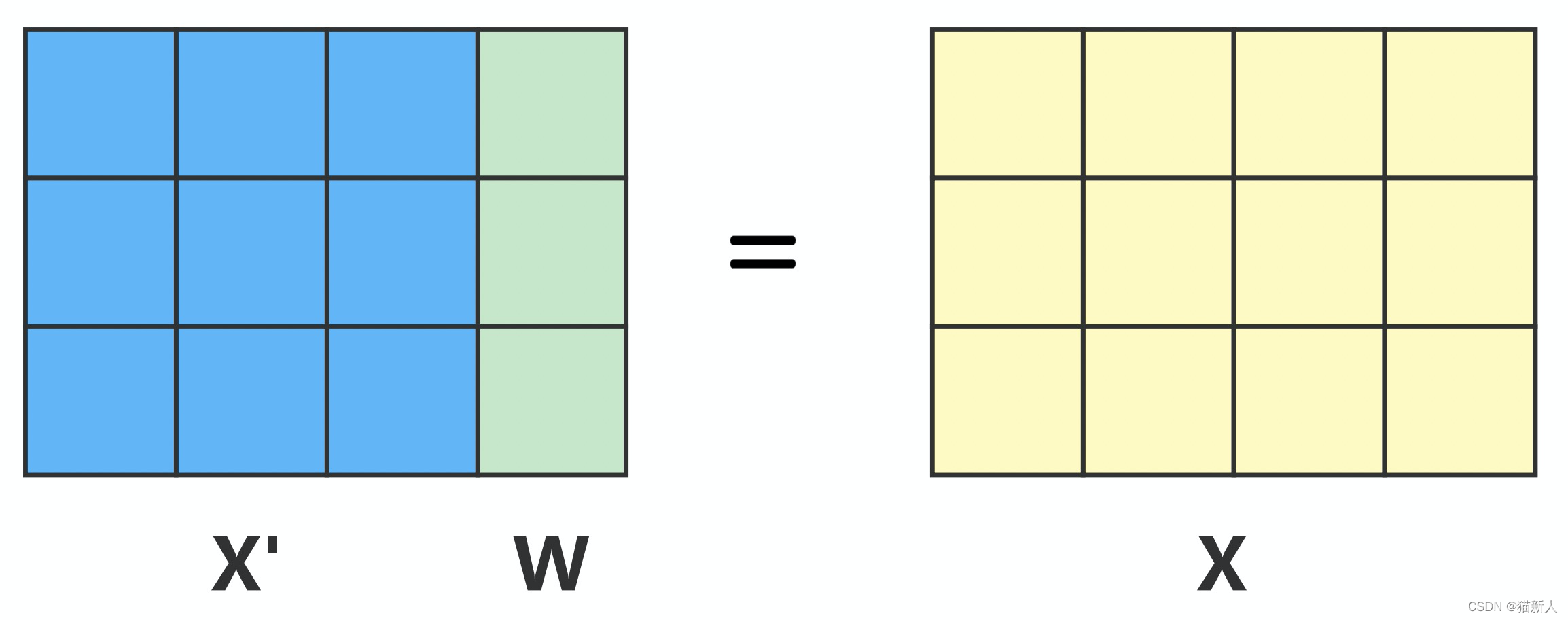
模型流程如下：
  步骤1: 将样本X’和W(干预动作)合并，训练模型
$$\mu (x,\omega ):=\mathbb{E}[Y^{obs}|X=x,W=\omega ]$$
  步骤2: 将待计算样本x，加入不同W取值，从而计算实验组所带来的提升（不同实验组响应率-对照组响应率）
$${\hat{\tau }}_S(x)=\hat{\mu }(x,1)-\hat{\mu }(x,0)$$

  S-Learner方法简单，且也可以使用常见模型作为基模型如XGBoost、LightBGM和NN等，但其本身仍然是响应模型，模型的效果取决于特征W的贡献度，若W的贡献度较低，则有可能会被模型过滤，导致Uplift Score为0。

S-Learner Python使用

from xgboost.sklearn import XGBClassifier
from causalml.inference.meta import BaseSClassifier
from causalml.dataset import make_uplift_classification
from sklearn.model_selection import train_test_split
df, x_names = make_uplift_classification(treatment_name=['control', 'treatment'])
df_train, df_test = train_test_split(df, test_size=0.2, random_state=111)
base_model = XGBClassifier()
clf = BaseSClassifier(learner=base_model,control_name='control')
clf.fit(df_train[x_names].values,
                 treatment=df_train['treatment_group_key'].values,
                 y=df_train['conversion'].values)
y_pred = clf.predict(df_test[x_names].values)
1
2
3
4
5
6
7
8
9
10
11
12

2.3 X-Learner

论文地址：https://arxiv.org/pdf/1706.03461.pdf
  X-Learner是在T-Learner的基础上优化的一种方法，利用了全量的数据进行预测，且对于Treatment和Control样本不平衡时，也有较好的效果。模型步骤如下：
  步骤1: 使用实验组和对照组数据分别训练模型(此处与T-learner一样)：
$$\begin{gathered} {\mu }_0(x)=\mathbb{E}[Y(0)|X=x] \\ {\mu }_1(x)=\mathbb{E}[Y(1)|X=x] \end{gathered}$$
  步骤2: 分别将实验组模型在对照组上的uplift和对照组模型在实验组上的uplift ：
$$\begin{gathered} {\tilde{D}}_i^1:=Y_i^1-{\hat{\mu }}_0(X_i^1) \\ {\tilde{D}}_i^0:=Y_i^0-{\hat{\mu }}_1(X_i^0) \end{gathered}$$
  步骤3: 根据步骤2中得到uplift score，使用回归算法拟合：
$$\begin{gathered} {\hat{\tau }}_0(x)=\mathbb{E}[{\tilde{D}}^0|X=x] \\ {\hat{\tau }}_1(x)=\mathbb{E}[{\tilde{D}}^1|X=x] \end{gathered}$$
  步骤4: 加权计算CATE估计量：
$${\hat{\tau }}_X(x)=g(x){\hat{\tau }}_0(x)+(1-g(x)){\hat{\tau }}_1(x)$$
  其中，g取值在[0,1]之间

X-Learner Python使用

from xgboost.sklearn import XGBClassifier,XGBRegressor
from causalml.inference.meta import BaseXClassifier
from causalml.dataset import make_uplift_classification
from sklearn.model_selection import train_test_split
df, x_names = make_uplift_classification(treatment_name=['control', 'treatment'])
df_train, df_test = train_test_split(df, test_size=0.2, random_state=111)

clf = BaseXClassifier(outcome_learner=XGBClassifier(),effect_learner=XGBRegressor(),control_name='control')
clf.fit(df_train[x_names].values,
                 treatment=df_train['treatment_group_key'].values,
                 y=df_train['conversion'].values)
y_pred = clf.predict(df_test[x_names].values)
1
2
3
4
5
6
7
8
9
10
11
12

2.4 Causal Tree

论文地址：https://link.springer.com/content/pdf/10.1007%2Fs10115-011-0434-0.pdf
  推理树是一种直接优化uplift的方法，算法是在决策树的基础上，改变叶节点的分裂方法，从而得到Uplift Tree。在预测环节，计算样本所在叶节点的实验组与对照组的差作为uplift score，公式如下所示（单Treatment）：
$$\hat{\tau }(x)=\frac{{\sum }_{i:T_i=1,X_i\in l}{Y}_i}{|i:T_i=1,X_i\in l|}-\frac{{\sum }_{i:T_i=0,X_i\in l}{Y}_i}{|i:T_i=0,X_i\in l|}$$
  其中，T=0为对照组，T=1为实验组，$X_i\in l$为落在叶节点l上的样本
  叶节点的分裂标准有多种，本文主要介绍Rzepakowski 和Jaroszewicz提出的基于信息论的分裂方法，公式如下。
$$D_{gain}(A)=D(P^T(Y):P^C(Y)|A)-D(P^T(Y):P^C(Y))$$
  其中，Pt和Pc是实验组和对照组的概率分布，函数D()评估实验组和对照组样本的差异，从而计算出分裂前后的发散增益程度。目前，评估叶节点的差异评估方法有相对殇（Kullback）、欧式距离（Euclidean）、卡方检验（Chi-Squared）和CTS，公式如下：
$$\begin{gathered} KL(P:Q)=\sum _{i=left,right}{p}_{i}log\frac{p_i}{q_i} \\ E(P:Q)=\sum _{i=left,right}(p_i-q_i{)}^2 \\ {\chi }^2(P:Q)=\sum _{i=left,right}\frac{(p_i-q_i{)}^2}{q_i} \end{gathered}$$
Causal Tree Python使用

from causalml.inference.tree import UpliftTreeClassifier
from causalml.dataset import make_uplift_classification
from sklearn.model_selection import train_test_split
df, x_names = make_uplift_classification(treatment_name=['control', 'treatment'])
df_train, df_test = train_test_split(df, test_size=0.2, random_state=111)

clf = BaseXClassifier(outcome_learner=XGBClassifier(),effect_learner=XGBRegressor(),control_name='control')
clf.fit(df_train[x_names].values,
                 treatment=df_train['treatment_group_key'].values,
                 y=df_train['conversion'].values)
y_pred = clf.predict(df_test[x_names].values)
1
2
3
4
5
6
7
8
9
10
11

参考

[1]Künzel S R, Sekhon J S, Bickel P J, et al. Metalearners for estimating heterogeneous treatment effects using machine learning[J]. Proceedings of the national academy of sciences, 2019, 116(10): 4156-4165.
[2]Rzepakowski P, Jaroszewicz S. Decision trees for uplift modeling with single and multiple treatments[J]. Knowledge and Information Systems, 2012, 32(2): 303-327.