热门标签
当前位置: article > 正文
【机器人工具箱学习笔记】第二章 位置与姿态描述_transl机器人工具箱
作者:花生_TL007 | 2024-02-16 21:19:41
赞
踩
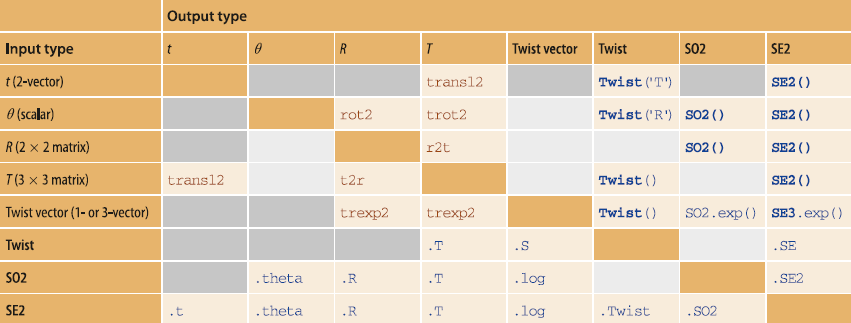
transl机器人工具箱
- rot2()%旋转矩阵
- det()%矩阵的模
- syms %定义变量
- simplify() %简述
- logm() %矩阵对数
- expm() %矩阵指数
- skew() %构造反对称指数
- vex() %skew()的逆运算
- transl2()%二维平移
- trot2()%二维旋转
- SE2() %齐次变换
- axis() %绘制坐标
- plotvol()%绘制坐标
- trplot2() %绘制二维齐次变换
- P=[] %定义一个点
- plot_point() %加入图中
- inv()%矩阵求逆
- double(inv())*[P;1] %求点相对于坐标系的坐标
- h2e() %e2h将欧几里得点转换为齐次坐标形式,h2e进行逆转换
- homtrans(T,P) %将齐次变换T应用于按列存储在P中的点
- eye() %单位矩阵
- Twist() %Twist就是Twist
- tw.T()%将Twist tw转为SE()
- tw.pole%求Twist tw的旋转中心点
- rotx() %以x为转轴的旋转矩阵
- trplot() %绘制相应的三维坐标系
- tranimate() %旋转动画
- eul2r() %ZYZ欧拉角表示的旋转矩阵
- tr2eul() %找到给定矩阵的欧拉角
- rpy2r() %RPY角表示的旋转矩阵
- tr2rpy() %找到给定矩阵的rpy角
- oa2r() %利用双向量表示法定义坐标系
- tr2angvec() %由旋转矩阵定义旋转的角度大小和绕其旋转的向量
- eig() %求矩阵的特征值和特征向量
- angvec2r() %从角度和向量计算出相应的旋转矩阵
- trlog() %分别返回旋转轴和旋转角
- UnitQuaternion() %单位四元数
- q.norm %四元数的大小
- q*q %四元数的乘法
- q.inv() %求四元数的共轭
- q.R %四元数转化为一个正交旋转矩阵
- q.plot() %绘制一个四元数所指的方向
- trotx()%绕x轴旋转()的齐次变换矩阵
- t2r() %提取旋转部分
- transl() %提取平移部分
- trnorm()%规范化

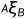 {B}相对于A的相对位姿/对{A}施加平移和旋转使它转化为{B}
{B}相对于A的相对位姿/对{A}施加平移和旋转使它转化为{B}
2.1标准正交旋转矩阵
- >> R = rot2(0.2) %弧度为2的旋转矩阵
- >> det(R) %矩阵的模
- >> det(R*R) %相乘后模仍为1
- ans =
- 1
- >> syms theta %工具箱支持符号变量
- >> R = rot2(theta)
- >> simplify(R*R) %简明表示
- >> simplify(det(R))
2.2矩阵指数
- >> R = rot2(0.3)
- R =
- 0.9553 -0.2955
- 0.2955 0.9553
- >> skew(2) %构造反对称矩阵
- ans =
- 0 -2
- 2 0
- >> vex(ans) %反对称矩阵的逆运算
- ans =
- 2
- %可使用logm和vex找到旋转矩阵的旋转角
- >> S = logm(R) %计算矩阵R的对数
- S =
- 0 -0.3000
- 0.3000 0
- >> vex(S) %找到反对称矩阵的元素
- ans =
- 0.3000
- >> expm(S) %logm的逆运算 构造标准正交旋转矩阵
- ans =
- 0.9553 -0.2955
- 0.2955 0.9553
- >> R = rot2(0.3);
- >> R = expm( skew(0.3) ); %与rot2(0.3)等价

由【3B1B笔记】e的矩阵指数——怎么算?为什么?知: ,即R = expm(skew(θ) ),也即
,即R = expm(skew(θ) ),也即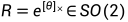
2.3齐次变换矩阵
- >> T1=SE2(1,2,30*pi/180)
- 或>> T1 = transl2(1, 2) * trot2(30, 'deg')
- >> axis([0 5 0 5]);
- 或>> plotvol([0 5 0 5]); %创建2D图并设置边界
- >> trplot2(T1, 'frame', '1', 'color', 'b') %绘制齐次变换
- >> T2 = transl2(2, 1)
- >> trplot2(T2, 'frame', '2', 'color', 'r');
- %复合运算的不可交换性
- >> T3 = T1*T2
- >> trplot2(T3, 'frame', '3', 'color', 'g');
- >> T4 = T2*T1;
- >> trplot2(T4, 'frame', '4', 'color', 'c');
- >> P = [3 ; 2 ]; %定义一个点
- >> plot_point(P, 'label', 'P', 'solid', 'ko'); %求在该点相对于坐标系1的坐标
- >> P1 = inv(T1) * [P; 1] %对点P附加一个1将欧几里得点转换为齐次形式
- >> h2e( inv(T1) * e2h(P) ) % e2h将欧几里得点转换为齐次坐标形式,h2e进行逆转换
- >> homtrans( inv(T1),P) %将齐次变换inv(T1)应用于按列存储在P中的点

2.4旋转
- >> plotvol([-5 4 -1 5]);
- >> T0 = eye(3,3);
- >> trplot2(T0, 'frame', '0');
- >> X = transl2(2, 3);
- >> trplot2(X, 'frame', 'X');
- >> R = trot2(2);
- >> trplot2(R*X, 'framelabel', 'RX', 'color', 'r');
- >> trplot2(X*R, 'framelabel', 'XR', 'color', 'r');
- >> C = [1 2]';
- >> plot_point(C, 'label', ' C', 'solid', 'ko')'
- >> RC = transl2(C) * R * transl2(-C)
- >> trplot2(RC*X, 'framelabel', 'XC', 'color', 'r');

RX绕原点旋转,而XR绕X点旋转。
而对于绕C旋转的XC,从右向左读,先将C点转换到原点,绕C旋转,然后再将坐标系平移回C
2.5 Twist
- >>tw = Twist('R',C)%以R为旋转扭,C为旋转中心点的坐标变换
- tw =
- ( 2 -1; 1 )
- >>tw.T(2)%沿twist中心点旋转2弧度的旋转矩阵
- ans =
- -0.4161 -0.9093 3.2347
- 0.9093 -0.4161 1.9230
- 0 0 1.0000
- >>tw.pole' %求twist的旋转中心点
- ans =
- 1 2
- >>tw = Twist('T', [1 1]) %纯平移的twist
- tw =
- ( 0.70711 0.70711; 0 )
- >>tw.T(sqrt(2)) %对纯平移的twist,参数为根2,变换矩阵为
- ans =
- 1 0 1
- 0 1 1
- 0 0 1
- >> T = transl2(2, 3) * trot2(0.5) %任意坐标变换矩阵
- T =
-
- 0.8776 -0.4794 2.0000
- 0.4794 0.8776 3.0000
- 0 0 1.0000
- >>tw = Twist(T) %将SE(2)转为twist,我们注意到C=0.5,即这不是一个单位twist
- tw =
- ( 2.7082 2.4372; 0.5 )
- >> tw.T %所以将其转换为一个二维坐标变换时不需要提供旋转角度这个参数
- ans =
- 0.8776 -0.4794 2.0000
- 0.4794 0.8776 3.0000
- 0 0 1.0000

二维twist的中心思想即为:任何坐标变换均为绕某点的旋转?
欧拉角:ZYZ序列 eul2r
横滚-俯仰-偏航角(卡尔丹角/泰特-布莱恩角/导航角): XYZ序列 rpy2r
双向量表示法: 接近向量 oa2r
3.1正交旋转矩阵
- >> R = rotx(pi/2) %以x为转轴的旋转矩阵
- >> trplot(R)
- >> tranimate(R) %旋转动画
- >> R = rotx(pi/2) * roty(pi/2)
- >> roty(pi/2)*rotx(pi/2) %证明旋转的不可交换性
3.2三角度表示法
- >> R = rotz(0.1) * roty(0.2) * rotz(0.3);
- >> R = eul2r(0.1, 0.2, 0.3) %计算欧拉角为(0.1, 0.2, 0.3)的等价旋转矩阵
- >> gamma = tr2eul(R) %找到给定矩阵的欧拉角
- >> R = eul2r(0.1 , -0.2, 0.3) %但如果θ为复数时
- >> tr2eul(R) %其反函数结果与原来不同
- ans =
- -3.0416 0.2000 -2.8416
- >> eul2r(ans) %但旋转矩阵相同
- >> R = eul2r(0.1, 0, 0.3)
- >> tr2eul(R) %对于θ=0的情况,与奇异点有关
- >> R = rpy2r(0.1, 0.2, 0.3) %计算RPY角为(0.1, 0.2, 0.3)的等价旋转矩阵
- >> gamma = tr2rpy(R) %找到给定矩阵的RPY角
3.3双向量表示法
- >> a = [1 0 0]'; %接近向量
- >> o = [0 1 0]'; %姿态向量
- >> R = oa2r(o, a) %利用双向量表示法定义坐标系
3.4绕任意向量旋转
- >> R = rpy2r(0.1 , 0.2, 0.3);
- >> [theta, v] = tr2angvec(R) %由R定义旋转的角度大小和绕其旋转的向量
- theta =
- 0.3655
- v =
- 0.1886 0.5834 0.7900
- >> [x,e] = eig(R) %求矩阵的特征值和特征向量
- x =
- 0.6944 + 0.0000i 0.6944 + 0.0000i 0.1886 + 0.0000i
- -0.0792 - 0.5688i -0.0792 + 0.5688i 0.5834 + 0.0000i
- -0.1073 + 0.4200i -0.1073 - 0.4200i 0.7900 + 0.0000i
- e =
- 0.9339 + 0.3574i 0.0000 + 0.0000i 0.0000 + 0.0000i
- 0.0000 + 0.0000i 0.9339 - 0.3574i 0.0000 + 0.0000i
- 0.0000 + 0.0000i 0.0000 + 0.0000i 1.0000 + 0.0000i
- >> R = angvec2r(pi/2, [1 0 0]) %从角度和向量计算出相应的旋转矩阵

一个正交旋转矩阵总有一个实特征值=1,其相应的特征向量位于矩阵v中对应的列向量,这个向量就是旋转轴
3.5矩阵指数
- >> R = rotx(0.3)
- >> S = logm(R)
- >> vex(S)'
- ans =
- 0.3000 0 0
- >> [th,w] = trlog(R) %返回R的旋转角度和旋转轴
- th =
- 0.3000
- w =
- 1.0000
- 0
- 0
- >> expm(S)
- ans =
- 1.0000 0 0
- 0 0.9553 -0.2955
- 0 0.2955 0.9553
- >> R = rotx(0.3);
- >> R = expm( skew([1 0 0]) * 0.3 ); %与rotx(0.3)等价

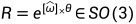 ,其中θ是转角,ω是平行于转轴的单位向量
,其中θ是转角,ω是平行于转轴的单位向量
注:三维斜对称矩阵:

3.6 四元数
Visualizing quaternions, an explorable video series
- >> q = UnitQuaternion( rpy2tr(0.1, 0.2, 0.3) ) %构造函数将传递的参数转换为四元数
- q =
- 0.98335 < 0.034271, 0.10602, 0.14357 >
- >> q.norm %四元数的大小
- ans =
- 1
- >> q = q * q; %四元数的乘法通过重载乘法运算符调用
- >> inv(q) %求四元数的共轭
- >> q*inv(q)
- >> q/q %四元数乘以它的倒数得到单位四元数
- ans =
- 1 < 0, 0, 0 >
- >> q.R %四元数转化为一个正交旋转矩阵
- >> q.plot() %绘制一个四元数所指的方向
- >> q*[1 0 0]' %一个向量可以被一个四元数旋转
3.7 4*4齐次变换
- %变换的合成
- >> T = transl(1, 0, 0) * trotx(pi/2) * transl(0, 1, 0)
- %提取旋转部分
- >> t2r(T)
- %提取平移部分
- >> transl(T)'
- %规范化
- >> R = trnorm(R);
区别:3*3标准正交与4*4齐次变换
3.8 Twists
- >> tw = Twist('R', [1 0 0], [0 0 0]) %单旋转,ω为1
- tw =
- ( 0 0 0; 1 0 0 )
- >> tw.T(0.3)
- ans =
- 1.0000 0 0 0
- 0 0.9553 -0.2955 0
- 0 0.2955 0.9553 0
- 0 0 0 1.0000
- >> tw = Twist('T', [0 1 0]) %单平移,ω为0,v为1
- tw =
- ( 0 1 0; 0 0 0 )
- >> tw.T(2)
- ans =
- 1 0 0 0
- 0 1 0 2
- 0 0 1 0
- 0 0 0 1
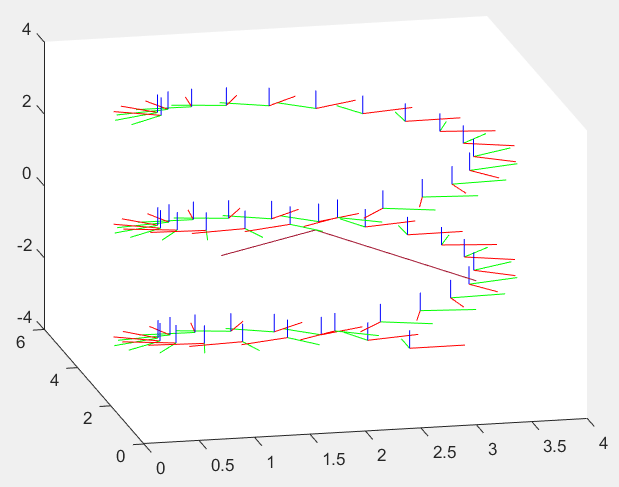
- >> X = transl(3, 4, -4);
- >> angles = [0:0.3:15];
- >> tw = Twist('R', [0 0 1], [2 3 2], 0.5);
- >> tranimate( @(theta) tw.T(theta) * X, angles, ...
- 'length', 0.5, 'retain', 'rgb', 'notext');
- >> T = transl(1, 2, 3) * eul2tr(0.3, 0.4, 0.5);
- >> tw = Twist(T)
- tw =
- ( 1.1204 1.6446 3.1778; 0.041006 0.4087 0.78907 )
- >> tw.pitch
- ans =
- 3.2256
- >> tw.theta
- ans =
- 0.8896
- >> tw.pole'
- ans =
- 0.0011 0.8473 -0.4389



声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/花生_TL007/article/detail/96764
推荐阅读
相关标签


