- 1yolov8/yolov7/yolov5-车辆测距+前车碰撞预警(追尾预警)+车辆检测识别+车辆跟踪测速(原创算法-毕业设计)_yolo测距
- 2C# list 成员对象是int型存在堆区还是栈区
- 3“探秘JS加密算法:MD5、Base64、DES/AES、RSA你都知道吗?”_js md5
- 4win10安装mysql-8.0.12-winx64解压版
- 5python for ArcGIS 绘制苏州市板块地图_苏州市arcgis地图
- 6Pytorch nn.Module_pytorch中nn模块
- 7深度:蚂蚁金融科技全面开放战略背后的技术布局
- 8程序员为什么不习惯关电脑?
- 9最前端|手把手教你打造前端规范工程
- 10RTL Project Directory_rtlproject
机器学习实战笔记(二)KNN算法_knn算法的距离度量采用方法
赞
踩
算法概念、基本思想和应用
概念
官方概念:所谓K近邻算法,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,就把该输入实例分类到这个类中。
简单来说,根据待分类点的周围邻居来判断类别,邻居大多数属于哪一类,就将待分类点归为哪一类。
简单示例
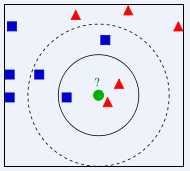
上图中绿色的点为待分类点,我们的任务是对它进行分类,判断它是属于蓝色正方形,还是红色三角形。如果我们设K=3,就找离它最近的3个邻居,我们发现3个邻居中红色三角形占多数,所以我们将它归类为红色三角形。如果我们设K=5,就找离它最近的5个邻居,发现5个邻居中蓝色正方形占多数,所以我们将它归类为蓝色正方形。
通过这个示例,你可以发现K的取值,对分类结果有重要影响。实际上,KNN有三个基本要素:
- K的取值
- 距离度量
- 分类决策规则
这三者对分类结果都有重要影响。
基本思想
KNN的基本思想是:在训练集中数据和标签已知的情况下,输入测试数据,将测试数据的特征与特征集中对应的特征进行相互比较,找到训练集中与之最为相似的前K个数据,则该测试数据对应的类别就是K个数据中出现次数最多的那个类别。
应用实例
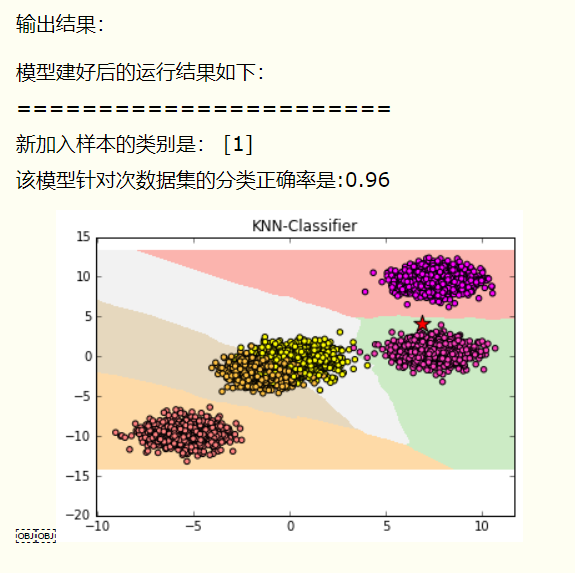
import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import make_blobs #make_blobs 聚类数据生成器 from sklearn.neighbors import KNeighborsClassifier #KNeighborsClassfier K近邻分类 #sklearn 基于Python语言的机器学习工具,支持包括分类,回归,降维和聚类四大机器学习算法。 # 还包括了特征提取,数据处理和模型评估者三大模块。 # sklearn.datasets (众)数据集;sklearn.neighbors 最近邻 data=make_blobs(n_samples=5000,centers=5,random_state=8) # n_samples 待生成样本的总数,sample 样本,抽样 # centers 要生成的样本中心数 # randon_state 随机生成器的种子 X,y=data #返回值,X 生成的样本数据集;y 样本数据集的标签 plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.spring,edgecolor='k') #c颜色,cmap Colormap实体或者是一个colormap的名字,cmap仅仅当c是一个浮点数数组的时候才使用。 clf=KNeighborsClassifier() clf.fit(X,y) x_min,x_max=X[:,0].min()-1,X[:,0].max()+1 y_min,y_max=X[:,1].min()-1,X[:,1].max()+1 xx,yy=np.meshgrid(np.arange(x_min,x_max,0.02), np.arange(y_min,y_max,0.02)) Z=clf.predict(np.c_[xx.ravel(),yy.ravel()]) Z=Z.reshape(xx.shape) plt.pcolormesh(xx,yy,Z,cmap=plt.cm.Pastel1) plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.spring,edgecolor='k') plt.title('KNN-Classifier') plt.scatter(6.88,4.18,marker='*',s=200,c='r') plt.xlim([x_min,x_max]) print('模型建好后的运行结果如下:') print('=======================') print('新加入样本的类别是:',clf.predict([[6.72,4.29]])) print('该模型针对次数据集的分类正确率是:{:.2f}'.format(clf.score(X,y)))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
运行这段代码后,得到的结果如下:
三个基本要素
K的取值
先说结论,K的取值不能过大,也不能过小。K值过小,整体模型会变得复杂,容易发生过拟合。K值过大,整体模型会变得简单,使预测发生错误。
怎么确保K取值不大不小?—— 一个个试呗,哪个效果好选哪个!
怎么看效果好?—— 通过分类正确率来判断
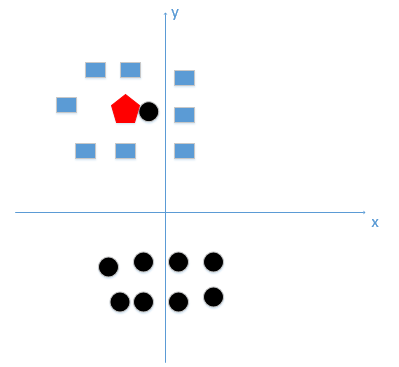
上图中,我们如果选的K值过小,假如K=1,那么分类结果就为黑色圆。下图中,我们如果选的K值过大,假如K=N,N很大,同样分类结果为黑色圆。
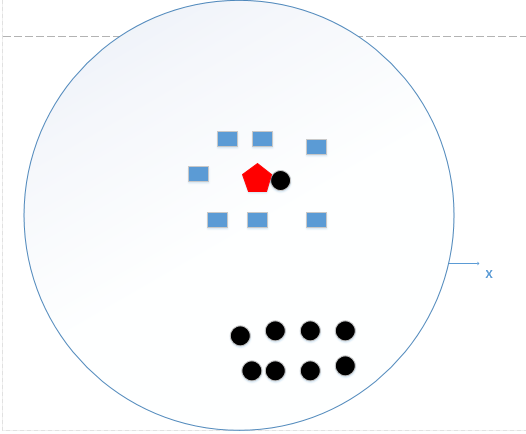
不大不小,效果才好,如下图,分类结果为蓝色矩形。
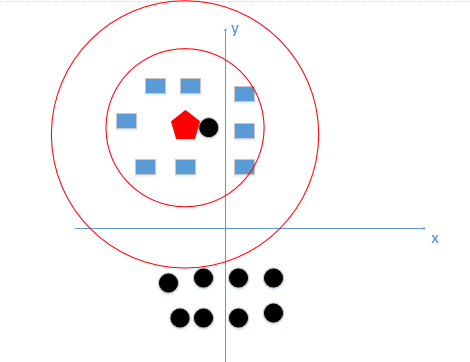
距离度量
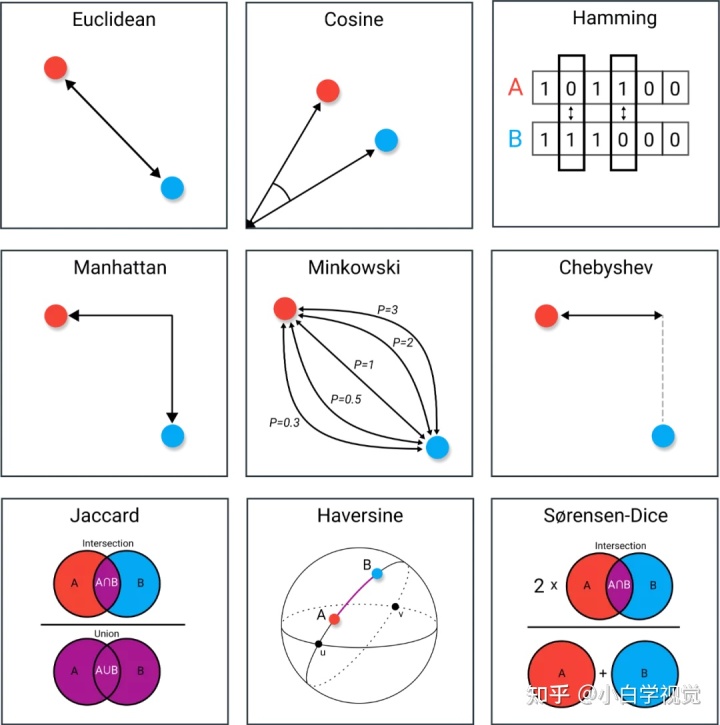
距离的度量方式有很多,上图中展示了9种度量方式,完整内容:一图看遍9种距离度量,图文并茂,详述应用场景! - 知乎 (zhihu.com)
KNN算法使用的距离度量方式为 L p L_{p} Lp

在实际应用中,距离函数的选择应该根据数据的特性和分析的需要而定,一般选取 L 2 L_{2} L2,即欧式距离表示。
分类决策规则
一般是少数服从多数。当选定K值时,通过距离计算得到最近的K个邻居,再计算它们当中所属类别的频率,待分类数据将被归为频率最高的类别。
特征归一化很重要
特征归一化不仅在KNN算法中,在其它算法的实现过程中也要重视。
所谓特征归一化,就是将不同类型的特征数值大小变为一致的过程。
举例:假设有4个样本及他们的特征如下:
| 样本 | 特征1 | 特征2 |
|---|---|---|
| 1 | 10001 | 2 |
| 2 | 16020 | 4 |
| 3 | 12008 | 6 |
| 4 | 13131 | 8 |
可见归一化前,特征1和特征2的大小不是一个数量级。此时,特征1对分类结果的影响要显著大于特征2。归一化后,特征变为:
| 样本 | 特征1 | 特征2 |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 1 | 0.33 |
| 3 | 0.73 | 0.67 |
| 4 | 0.81 | 1 |
算法描述与优缺点
KNN算法的描述:
- 计算测试数据与各个训练数据之间的距离;
- 按照距离的递增关系进行排序;
- 选取距离最小的K个点;
- 确定前K个点所在类别的出现频率
- 返回前K个点中出现频率最高的类别作为测试数据的预测分类。
算法优点
- 简单,易于理解,易于实现,无需估计参数
- 训练时间为零。它没有显示的训练,不像其它有监督的算法会用训练集train一个模型,然后验证集或测试集用该模型分类。KNN只是把样本保存起来,收到测试数据时再处理,所以KNN训练时间为零。
- 对数据没有假设,准确度高,对异常点不敏感
算法缺点
- 计算量太大,尤其是特征数多的时候
- 惰性学习方法,基本上不学习,导致预测时速度比起逻辑回归之类的算法慢
- 对训练数据依赖度特别大,容错性太差。如果训练集中,有数据是错误的,刚刚好又在需要分类的数值的旁边,这样就会直接导致预测的数据的不准确。
参考博客
一图看遍9种距离度量,图文并茂,详述应用场景! - 知乎 (zhihu.com)
机器学习–K近邻 (KNN)算法的原理及优缺点 - 泰初 - 博客园 (cnblogs.com)
一文搞懂k近邻(k-NN)算法(一) - 知乎 (zhihu.com)




