动态规划与负数取余过程 —— NC266925 我不是大富翁_rabbitrabbit 拿到了一张环形的大富翁地图,地图被平均划分为了 nn 个地块,地块的

题目来源：

牛客小白月赛88

题目如下：

题目 我不是大富翁
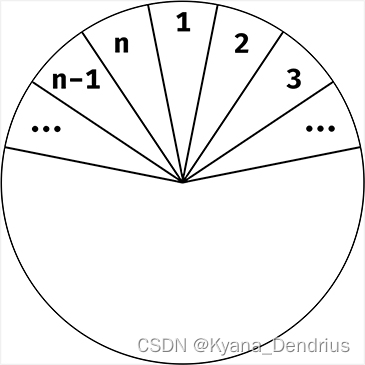
Rabbit 拿到了一张环形的大富翁地图，地图被平均划分为了 n 个地块，地块的编号以 1 为起点，顺时针进行排布。即 1 号地块的顺时针方向依次为 2, 3, …… 号地块；1 号地块的逆时针方向依次为 n, n−1, …… 号地块（由于是环形的，所以 1 号地块与 n 号地块相邻，如下图所示）。

游戏过程如下：系统会给定一个长度为 m 的行动力序列 ​ ，在第 i (1≤i≤m) 回合，Rabbit 都需要移动  个地块，但是他可以自由选择移动的方向（换句话说，可以自由选择是向逆时针还是顺时针方向移动 个地块）。
          在游戏的开始时，Rabbit 位于 1 号地块，他想知道是否存在这样一种移动方式，使得 m 个回合后他依旧在 1 号地块。

输入
每个测试文件仅有一组测试数据。
第一行输入两个整数 n 和 m (1≤n, m≤5000) 表示地块数量和行动回合数。
第二行输入 m 个整数 ​ () 表示行动力序列。

输出
如果 m 个回合后 Rabbit 依旧在 111 号地块，则输出 YES ；否则，请输出 NO 。您可以以任何大小写形式输出答案，例如，yEs 、yes 和 YeS 都将被视为肯定的回答。

尝试：深度优先搜索和部分优化：

在dfs函数中，在判断下一步之前先测试目前所在的步数是否能被剩余的步数抵消。

#include<bits/stdc++.h>
using namespace std;
bool found = false;
 
void dfs(int iptDeg,int m,int n,vector<int> steps,bool addorminus){
    if(found == false){
        int maxN = steps.size();
        int nextDeg = iptDeg;
        int left = accumulate(steps.begin()+n-1,steps.end(),0);
        if(left == iptDeg){found = true;return;}
        if(left < iptDeg){return;}
        if(n == maxN){
            if(iptDeg%m==0){
                found = true;
            }
            return;
        }
        int operation = steps[n-1];
        if(addorminus == false){operation = operation*(-1);}
        nextDeg = nextDeg + operation;
        dfs(nextDeg,m,n+1,steps,true);
        dfs(nextDeg,m,n+1,steps,false);
    }
}
 
 
int main(){
    int m,n;
    cin >> m >> n;
    vector<int> steps(n);
    for(int i=0;i<n;i++){
        cin >> steps[i];
    }
    dfs(0,m,1,steps,true);
    if(found == true){cout << "YES" << endl;}
    else cout << "NO" << endl;
    return 0;
}

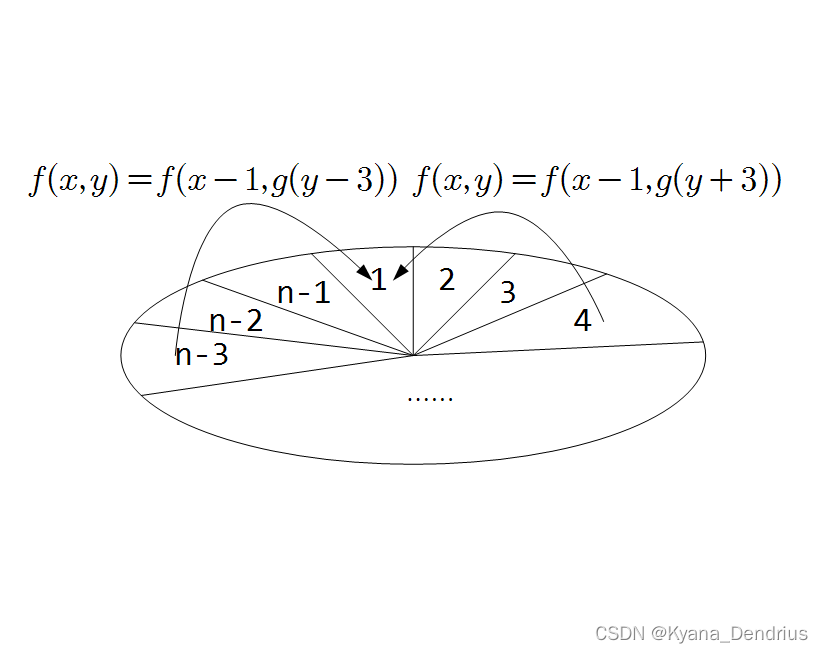
深度优先搜索本质是一种暴力枚举做法，其时间复杂度为，搜索算法在算法题中的作用极其有限，不应当优先考虑。考虑动态规划：如果在第m步走到了起点，那么第m-1步应该在满足距离起点为行动力序列中的的位置上，故可以构建状态转移方程：

f(x)返回布尔值：true为该状态存在，false为该状态不存在。

g(x)的作用是把转换到圆盘上合适的位置。

完整代码如下：

#include<bits/stdc++.h>
using namespace std;
 
 
int main(){
    int m,n;
    cin >> n >> m;
    vector<int> steps(m);
    for(int i=0;i<m;i++){
        cin >> steps[i];
    }
    vector<vector<bool>> dp(m+1,vector<bool>(n,false));
    dp[0][0] = true;
    for(int i=1;i<=m;i++){
        for(int j=0;j<n;j++){
            if (dp[i - 1][j] == true) {
                dp[i][(j+steps[i-1])%n] = true;
                dp[i][(n+((j-steps[i-1])%n))%n] = true;
            }
        }
    }
    if(dp[m][0]) cout << "YES" << endl;
    else cout << "NO" << endl;
    return 0;
}

值得注意的是C++的取余操作的具体过程：

if (dp[i - 1][j]) {
    dp[i][(j+steps[i-1])%n] = true;
    dp[i][(n+((j-steps[i-1])%n))%n] = true;
}

一开始的代码为：

if (dp[i - 1][j]) {
    dp[i][(j + steps[i - 1]) % n] = true;
    dp[i][(j - steps[i - 1]) % n] = true;
}

这会导致数组越界，因为负数%正数会导致结果为负数，C++的取余操作基于整除操作，众所周知：C++的整数除法是截断取整，即：

取余的操作即：

由此可知取余的结果符号和被取余的数的符号相同，同时结果的绝对值小于被取余数的绝对值。

该算法的复杂度为。

感谢你能看到这里。

参考文章：

C++ 负数取余-CSDN博客