在这个函数中，fun为目标函数，x0为处值，必须为实数，可任意选择，原因在其他博客上看到是不影响全局最优解和局部最优解的选择。A，b为 $Ax\leqslant b$ 中的系数矩阵与向量。Aeq和beq是线性约束中的等式。lb为变量的下界，ub为变量的上界。nonlcon为[]是在没有非线性约束和等式的情况下，options是优化选择参数。

4.形式化问题（来源：川川菜鸟）

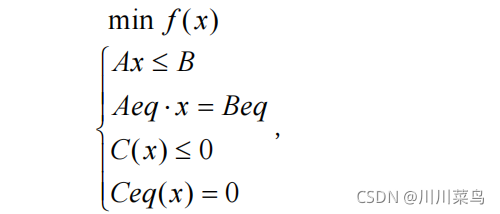
二、函数定义方法

1.符号定义法


syms x;            %定义变量x
f(x)=x+sin(x);     %定义函数f(x)
subs(f(x),x,pi/2)  %置换函数subs可以将变量进行替换处理，即带入变量进行求解或变量代换
ans =
pi/2 + 1

2.内联函数定义法


fx=inline('x+sin(x)')
 
fx =
 
     内联函数:
     fx(x) = x+sin(x)
 
fx(pi/2)

3.匿名函数定义法


clear
fx=@(x)x+sin(x);
fx(pi/2)
ans =
    2.5708

三、实例

3.1实例1

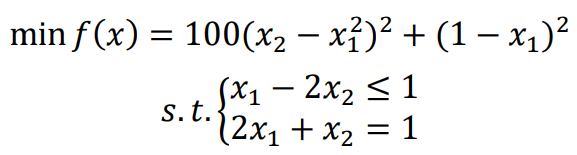
3.1.1分析

首先，我们可以发现其中目标函数为非线性函数，对于约束条件都是线性的，所以在这里只需要定义目标函数即可，此外操作如线性规划。

3.1.2Matlab求解


clear
f=@(x)100*(x(2)-x(1)^2)^2+(1-x(1))^2;      %定义非线性目标函数
a=[1 -2];b=[1];                            %线性约束条件的不等式系数矩阵
aeq=[2 1];beq=[1];                         %线性约束条件的等式系数矩阵
[x,yval]=fmincon(f,[0,1],a,b,aeq,beq)      %非线性规划的全局范围最优解

3.1.2运行结果


Local minimum found that satisfies the constraints.
 
Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the optimality tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.
 
<stopping criteria details>
 
x =
    0.4149    0.1701
yval =
    0.3427

因此，最优化的解是x1=0.4149，x2=0.1701，目标函数最优值为0.3427。

3.2实例2（来源@皮皮冬）

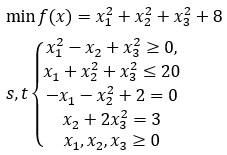
3.2.1分析

可以发现，此问题是求解最小值优化问题，所以对于相关系数不必做取负号处理，对于约束条件，无线性规划条件，所以A,b,Aeq,beq都为空元素。另外，约束条件中有非线性条件，不仅有不等式，也包括等式存在，所以对其需做进一步处理。在这里采用.mat文件的方式定义函数，函数调用过程中求解最优解。

3.2.2Matlab求解

1.对非线性目标函数做fun1.mat文件定义。


function f = fun1( x )      %f为返回结果，fun1为函数名，x为自变量（输入参数）
f=sum(x.^2)+8               %函数
end

2.对非线性约束条件做fun2.mat文件定义。


function [ g,h] = fun2( x )              %输入参数x，fun2函数名，g为非线性不等式，h为非线性等式
g=[-x(1)^2+x(2)-x(3)^2,x(1)+x(2)^2+x(3)^2-20];   %非线性不等式的结果矩阵g 
h=[x(2)+2*x(3)^2-3,-x(1)-x(2)^2+2];              %非线性等式的结果矩阵h
end

3.命令行窗口调用求解


clear
x0=[1,1,1];
lb=[0,0,0];
ub=[inf,inf,inf];
A=[];b=[];Aeq=[];beq=[];
[x,fval]=fmincon('fun1',x0,A,b,Aeq,beq,lb,ub,'fun2')

3.2.3运行结果


x =
    0.5522    1.2033    0.9478
fval =
   10.6511

四、总结

通过今天的学习，确实，受益匪浅，对于非线性规划，实际建模过程中经常遇到二次方，三次方之类的题目。同时，对于我以前的疑惑有以下几个问题：

1.如果不是不等式之类的约束条件，而是微分方程之类的约束条件，该如何求解？

2.对于分段函数求最优解，是否可采用分枝定界法进行联立？

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/花生_TL007/article/detail/350657