代码随想录算法训练营第二十三天（二叉树9）|669. 修剪二叉搜索树、108. 将有序数组转换为二叉搜索树、538. 把二叉搜索树转换为累加树(JAVA)

---

669. 修剪二叉搜索树

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

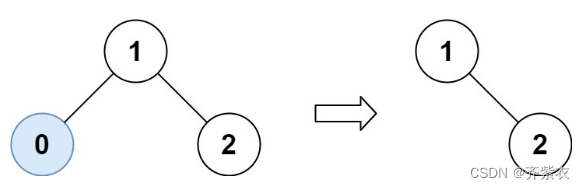
• 输入：root = [1,0,2], low = 1, high = 2
• 输出：[1,null,2]

示例 2：

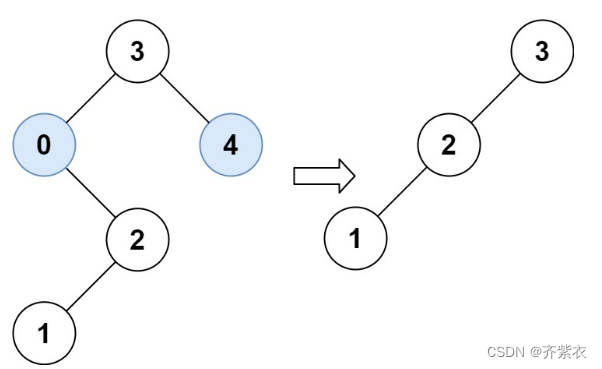
• 输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
• 输出：[3,2,null,1]

提示：

树中节点数在范围 [1, 10⁴] 内
0 <= Node.val <= 10⁴
树中每个节点的值都是 唯一 的
题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 10⁴

解题思路

通过遍历搜索不符合的节点然后重新插入

源码

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) {
            return null;
        }
        if (root.val < low) {
            return trimBST(root.right, low, high);
        }
        if (root.val > high) {
            return trimBST(root.left, low, high);
        }
        root.left = trimBST(root.left, low, high);
        root.right = trimBST(root.right, low, high);
        return root;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

---

108. 将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵
平衡
二叉搜索树。

示例 1：

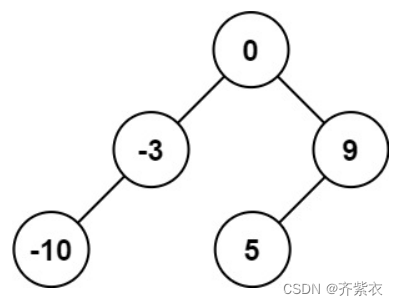
• 输入：nums = [-10,-3,0,5,9]
• 输出：[0,-3,9,-10,null,5]
• 解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：
  

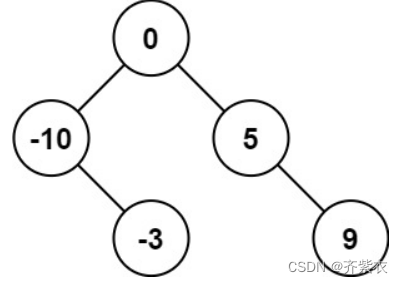
示例 2：

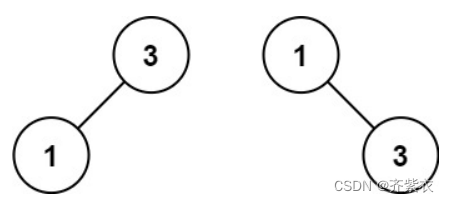
• 输入：nums = [1,3]
• 输出：[3,1]
• 解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

• 1 <= nums.length <= 10⁴
• -10⁴ <= nums[i] <= 10⁴
• nums 按 严格递增 顺序排列

解题思路

取数组中间结点作为根节点进行构造，然后依次分割，形成平衡二叉树

源码

class Solution {
	public TreeNode sortedArrayToBST(int[] nums) {
		TreeNode root = traversal(nums, 0, nums.length - 1);
		return root;
	}
	
	private TreeNode traversal(int[] nums, int left, int right) {
		if (left > right) return null;

		int mid = left + ((right - left) >> 1);
		TreeNode root = new TreeNode(nums[mid]);
		root.left = traversal(nums, left, mid - 1);
		root.right = traversal(nums, mid + 1, right);
		return root;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

---

538. 把二叉搜索树转换为累加树

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。

示例 1：

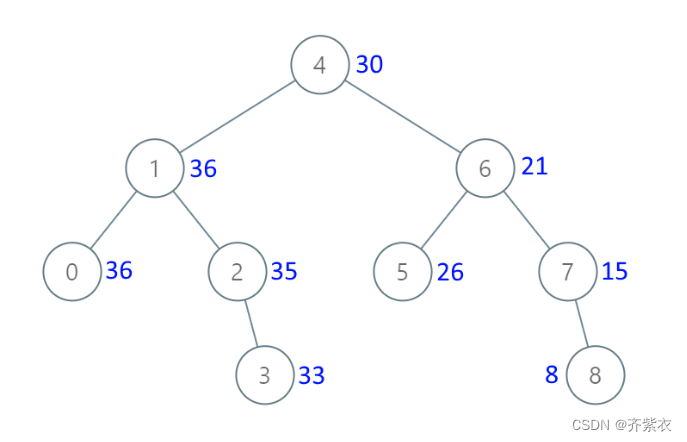
• 输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
• 输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

• 输入：root = [0,null,1]
• 输出：[1,null,1]

示例 3：

• 输入：root = [1,0,2]
• 输出：[3,3,2]

示例 4：

• 输入：root = [3,2,4,1]
• 输出：[7,9,4,10]

提示：

• 树中的节点数介于 0 和 10⁴ 之间。
• 每个节点的值介于 -10⁴ 和 10⁴ 之间。
• 树中的所有值 互不相同 。
• 给定的树为二叉搜索树。

解题思路

把它看成一个有序数组然后进行累加，反中序遍历（右中左）然后顺序累加就可以

源码

class Solution {
    int sum;
    public TreeNode convertBST(TreeNode root) {
        sum = 0;
        convertBST1(root);
        return root;
    }
    
    public void convertBST1(TreeNode root) {
        if (root == null) {
            return;
        }
        convertBST1(root.right);
        sum += root.val;
        root.val = sum;
        convertBST1(root.left);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

---