903. 昂贵的聘礼题解（建图挺有趣的）_年轻的探险家来到了一个印第安部落里

903. 昂贵的聘礼原题

年轻的探险家来到了一个印第安部落里。在那里他和酋长的女儿相爱了，于是便向酋长去求亲。酋长要他用 10000 个金币作为聘礼才答应把女儿嫁给他。探险家拿不出这么多金币，便请求酋长降低要求。酋长说：”嗯，如果你能够替我弄到大祭司的皮袄，我可以只要 8000 金币。如果你能够弄来他的水晶球，那么只要 5000 金币就行了。”探险家就跑到大祭司那里，向他要求皮袄或水晶球，大祭司要他用金币来换，或者替他弄来其他的东西，他可以降低价格。探险家于是又跑到其他地方，其他人也提出了类似的要求，或者直接用金币换，或者找到其他东西就可以降低价格。不过探险家没必要用多样东西去换一样东西，因为不会得到更低的价格。探险家现在很需要你的帮忙，让他用最少的金币娶到自己的心上人。另外他要告诉你的是，在这个部落里，等级观念十分森严。地位差距超过一定限制的两个人之间不会进行任何形式的直接接触，包括交易。他是一个外来人，所以可以不受这些限制。但是如果他和某个地位较低的人进行了交易，地位较高的的人不会再和他交易，他们认为这样等于是间接接触，反过来也一样。因此你需要在考虑所有的情况以后给他提供一个最好的方案。为了方便起见，我们把所有的物品从 1 开始进行编号，酋长的允诺也看作一个物品，并且编号总是 1。每个物品都有对应的价格 $P$，主人的地位等级 $L$，以及一系列的替代品$Ti$ 和该替代品所对应的”优惠”$Vi$。如果两人地位等级差距超过了$M$，就不能”间接交易”。你必须根据这些数据来计算出探险家最少需要多少金币才能娶到酋长的女儿。

输入格式
输入第一行是两个整数 $M$，$N$，依次表示地位等级差距限制和物品的总数。

接下来按照编号从小到大依次给出了 $N$ 个物品的描述。

每个物品的描述开头是三个非负整数 $P$、$L$、$X$，依次表示该物品的价格、主人的地位等级和替代品总数。

接下来 X 行每行包括两个整数 $T$ 和 $V$，分别表示替代品的编号和”优惠价格”。

输出格式
输出最少需要的金币数。

数据范围
$1\le N\le 100$,
$1\le P\le 10000$,
$1\le L,M\le N$,
$0\le X<N$
输入格式

1 4
10000 3 2
2 8000
3 5000
1000 2 1
4 200
3000 2 1
4 200
50 2 0

输出格式

5250

咳咳，本蒟蒻深夜做题，最短路刚刚入门（感觉这题还是挺有意思的），因此写这题时还是有很多感触的（从acwing上搬题，排版不好看，见谅）

解题思路

• 题意：首先，我们先来看题意，这是一道最短路（牵线 ）题，题意就是说一个旅行家要娶酋长的女儿，然后酋长要求他给足够的金币，或者用不同的物品可以使金币优惠（只能用一件物品），然后旅行家可不是就得找物品的主人要吗，物品的主人可好，一样的要求，可以以物抵物，也可以用金币购物，然后如此迭代，假设娶酋长的女儿为1号物品，后面的以此类推，共有n个物品，然后每个物品会给出它的替代品（即用这个替代品加优惠的金币可以交换这个物品），问旅行家最少能用多少金币取到酋长的女儿（不得不说，结个婚真难 ），接下来，我们不妨先模拟一下样例。（$le$代表等级，$id$代表编号）如下图
  
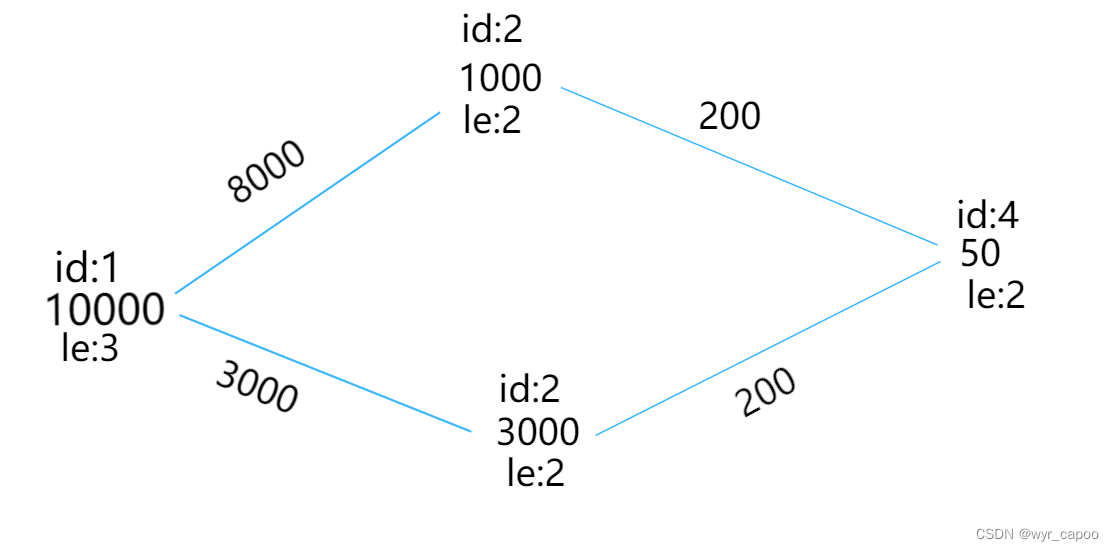
  这张图很好的描绘了各个物品之间的关系，但是此时我们忽略了一个问题，所有的物品我们都可以直接用金币解决的，所以，对于每个点，我们发现都多出来一条边，边权是物品本身的价格，如下图：
  
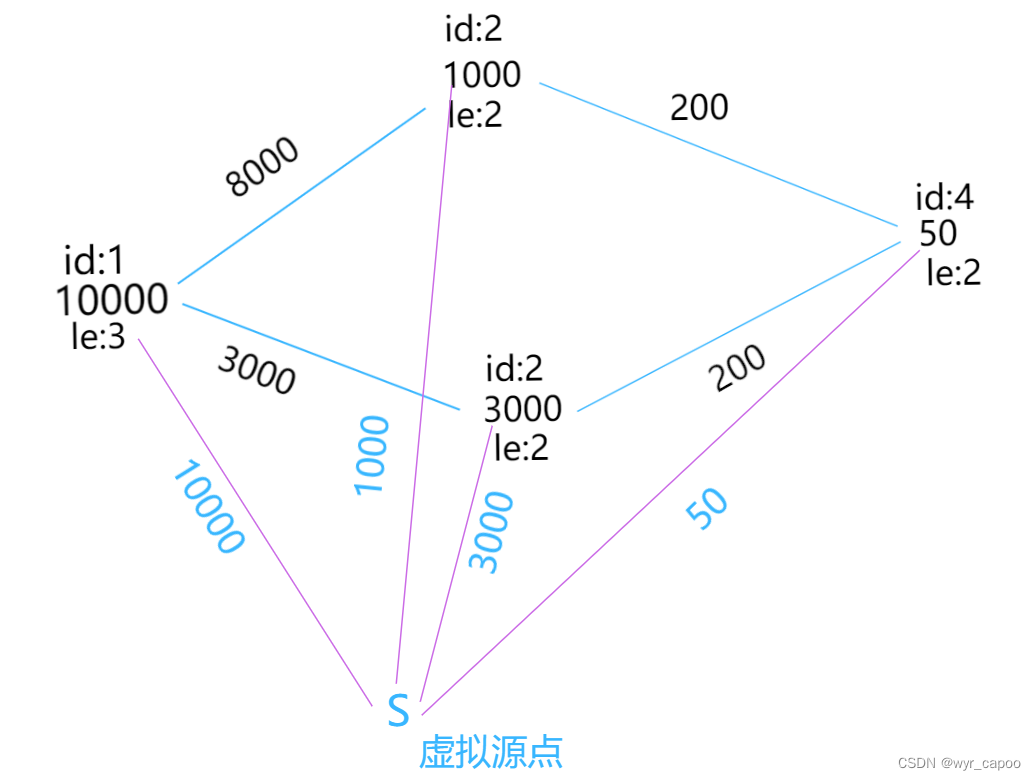
  将这个源点$S$定义成虚拟源点，从虚拟源点可以引出$n$条边，连向$n$个点，每条边的边权是每个点对应的价格，于是样例各个物品间的关系都确定了，那么这道题就可以转化成从虚拟源点$S$到1号点之间的最短路径，完成建图后，这题就转化成了最短路问题了。
• 思路：我来看一下数据范围，$N$是100数量级的，看地位等级差距限制也是100数量级的，我们来考虑一下各个算法的时间复杂度，朴素版$Dijkstra$时间复杂度是$O(n^2)$，由于有地位等级限制（我们之前并没有考虑这一点），所以我们必须保证每次交易的等级$level[i]$满足$|level[1]-m|\le level[i]\le |level[i]+m|$,（这样我们才能保证最后能跟1号点交换物品），所以我们可以跑$m$+1次$Dijkstra$，那么时间复杂度就是$O(n^{2}m)$，完全合理，不会超时，再看堆优化版的$Dijkstra$，边数是$n^2$级别的，所以最后总的时间复杂度是$O(n^{3}logn)$，也没问题，再看$SPFA$,正常情况下$SPFA$的复杂度是$O(m)$，最坏情况不会超过$O(n^3))$（本题边数是点数的平方），所以总的复杂度可能达到$O(n^4)$,但大部分情况是$O(n^3)$，所以我们也可以试一试，再看$Floyd$，时间复杂度妥妥的$O(n^4)$，所以大概率会$TLE$，因此我们就不用$Floyd$了（其实我也不会用$Floyd$写这题，轻点骂 ）

代码

废话说了那么多，最后还是上代码~~~

• 朴素版$Dijkstra$

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=110;
int w[N][N],dist[N],level[N],n,m,res=0x3f3f3f3f;
bool st[N];
int dij(int left,int right){
	memset(dist,0x3f,sizeof(dist));
	memset(st,0,sizeof st);//不要忘了memset，因为要m+1次 
	dist[0]=0;
	for(int i=1;i<=n;i++){
		int t=-1;
		for(int j=0;j<=n;j++){//j要从0开始，0是虚拟源点
			if(!st[j] && (t==-1 || dist[j]<dist[t])){
				t=j;
			}
		}
		st[t]=1;
		for(int j=1;j<=n;j++){
			if(level[j]>=left && level[j]<=right){
				dist[j]=min(dist[j],dist[t]+w[t][j]);
			}
		}
	}//Dijkstra模板 
	return dist[1];
}
int main(){
	memset(w,0x3f,sizeof w);
	cin>>m>>n;
	for(int i=1;i<=n;i++) w[i][i]=0;//i到i的点 
	for(int i=1;i<=n;i++){
		int price,cnt;
		cin>>price>>level[i]>>cnt;
		w[0][i]=min(w[0][i],price);//0到i之间连了一条价格为price的边
		                           //（min是防止重边） （虚拟源点设成0） 
		while(cnt--){
			int id,cost;
			cin>>id>>cost;
			w[id][i]=min(w[id][i],cost);//id到i之间连了一条边权为cost的边
		}
	}
	for(int i=level[1]-m;i<=level[1];i++){
		res=min(res,dij(i,i+m));//每个i即等级跑一遍Dijkstra 
	}
	cout<<res<<endl;
	return 0; 
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

• 堆优化版的$Dijkstra$

#include <iostream>
#include <cstring>
#include <queue>
#include <cstdio>
#include <vector>
using namespace std;
const int N=10010;//这里要存边，数据范围要开到10000+，不然会Segmentation Fault   
                  //（~~别问我怎么知道的~~）
int idx,e[N],n,m,ne[N],v[N],level[N],dist[N],h[N],res=0x3f3f3f3f;
bool st[N];
typedef pair<int,int> PII;
void add(int a,int b,int c){
	e[idx]=b,v[idx]=c,ne[idx]=h[a],h[a]=idx++;//邻接表存图 
}
int dij(int left,int right){
	memset(dist,0x3f,sizeof dist);
	memset(st,0,sizeof st);
	dist[0]=0;
	priority_queue<PII,vector<PII>,greater<PII>> heap;
	heap.push({0,0});//这里也一样，将0号点入队
	while(heap.size()){
		PII t=heap.top();
		heap.pop();
		int ver=t.second,distance=t.first;
		if(st[ver]) continue;
		st[ver]=1;
		for(int i=h[ver];i!=-1;i=ne[i]){
			int j=e[i];
			if(level[j]>=left && level[j]<=right){//同样要判断等级限制范围 
				if(dist[j]>distance+v[i]){
					dist[j]=distance+v[i];
					heap.push({dist[j],j}); 
				}
			}
		}
	}
	return dist[1];
}
int main(){
	cin>>m>>n;
	memset(h,-1,sizeof h);
	for(int i=1;i<=n;i++){
		int price,cnt;
		cin>>price>>level[i]>>cnt;
		add(0,i,price);//0到i建一条边权为price的边，min防止重边 
		while(cnt--){
			int id,cost;
			cin>>id>>cost;
			add(id,i,cost);
		}
	} 
	for(int i=level[1]-m;i<=level[1]+m;i++){
		res=min(res,dij(i,i+m));
	}
	cout<<res<<endl;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

• 最后是我最喜欢的$SPFA$（隔壁学校佬说是因为你没被卡过才最喜欢，嘶~ ）

#include <iostream>
#include <cstring>
#include <queue>
#include <vector>
using namespace std;
const int N=10010;
int idx,dist[N],e[N],ne[N],h[N],v[N],n,m,level[N],res=0x3f3f3f3f;
bool st[N];
void add(int a,int b,int c){
	e[idx]=b;
	v[idx]=c;
	ne[idx]=h[a];
	h[a]=idx++;
}
int spfa(int left,int right){
	memset(dist,0x3f,sizeof dist);
	memset(st,0,sizeof st);
	dist[0]=0;
	queue<int> q;
	q.push(0);
	st[0]=1;
	while(q.size()){
		int t=q.front();
		q.pop();
		st[t]=0;
		for(int i=h[t];i!=-1;i=ne[i]){
			int j=e[i];
			if(level[j]>=left && level[j]<=right){
				if(dist[j]>dist[t]+v[i]){
					dist[j]=dist[t]+v[i];
					if(!st[j]){
						q.push(j);
						st[j]=1;
					}
				}
			}
		}
	}
	return dist[1];
}
int main(){
	cin>>m>>n;
	memset(h,-1,sizeof h);
	for(int i=1;i<=n;i++){
		int price,cnt;
		cin>>price>>level[i]>>cnt;
		add(0,i,price);
		while(cnt--){
			int id,cost;
			cin>>id>>cost;
			add(id,i,cost);
		}
	}
	for(int i=level[1]-m;i<=level[1];i++) res=min(res,spfa(i,i+m));
	cout<<res<<endl;
	return 0;//思路与堆优化版的Dijkstra是一样的，就是把模板换了换
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

如果真有能看到这里的大佬，本蒟蒻真的十分感谢，因为也没怎么写过题解，如有错误，请大佬多多包涵（doge）（/拜谢//拜谢//拜谢/）！