【二叉树搜索树/二叉排序树】BST树的创建，插入，找最小结点的下一个节点/找最大结点的前驱

基本概念：

二叉树搜索树：【二叉排序树】

1. 每个结点都有一个作为搜索一句的关键码,所有的结点的关键码给互不相同
2. 左子树（如果存在）所有结点的关键码都小于根结点的关键码
3. 右子树（如果存在）所有结点的关键码都大于根节点的关键码
4. 左子树和右子树也都是二叉搜索树。

特点：说人话，大的放右边，小的放左边。

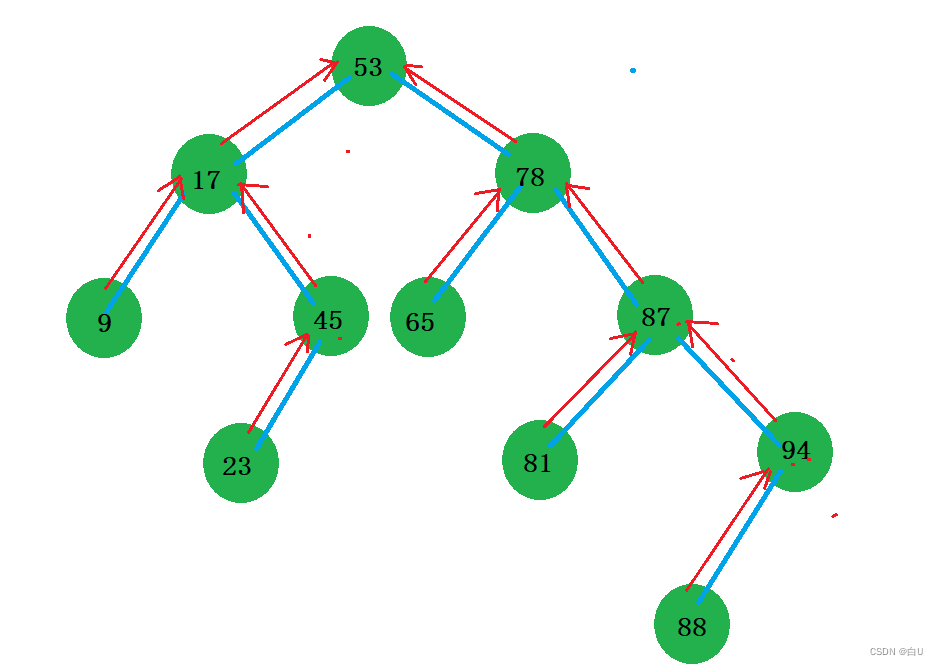
如果对一颗二叉排序树进行中序遍历，就可以按照从小到大的顺序，将各个结点的关键码排列。

创建一棵二叉排序树

有三个指向： parent ，leftchild，rightchild

二叉搜索树结构设计：

typedef int KeyType;
typedef struct {
     struct  BstNode* parent;
     struct  BstNode* leftchild;
     struct  BstNode* rightchild;
       KeyType* key;
}BstNode;
typedef struct 
{
    BstNode*root;
    int cursize;
 }BSTree;

1
2
3
4
5
6
7
8
9
10
11
12
13

查询函数：

BstNode FindValue(BSTree *tree,int kx)
{
   
   BStree *ptr = tree->root;
  while( ptr!= nullptr || ptr->key != kx)
  {
       ptr = ptr->key < kx ? ptr->leftchild:ptr->rightchild;
  }
  return ptr;
}
1
2
3
4
5
6
7
8
9
10

BstNode *Search(BstNode*ptr,KeyType kx)
{
    if(ptr == nullptr || ptr->key == kx) return ptr;
    else if(kx > ptr->key) { return Search(ptr->rightchild,kx);}
    else {return Search(ptr ->leftchild,kx);}
    }
BstNode *SearchValue(BSTree *ptree,KeyType kx)
{
   return Search(ptree->root ,KeyType kx)
}
1
2
3
4
5
6
7
8
9
10

插入思想：

1. 先插入根结点。
2. 插入后，开始判断根节点是否为空以及待插入的数是否等于当前结点的数，如果不等于空，则保存根节点，并判断kx的值小于还是大于key
3. 如果大于，走右边，小于走左边，再次判断如果满足当前结点不为空，是否和当前结点的key值相等，相同返回false
4. 否则为空，申请结点，存入kx，并将双亲结点指向它的根结点
5. 判断，小于根的左孩子指向它，大于右孩子指向它。

**加个引用就可以改变root int p = &a; int &s = p; 作为s指针p的别名

bool Insert(BstNode *&ptr, KeyType kx)
{
	/*if (ptr == NULL) //先判定 ptr是否为空，如果为空
	{
		ptr = MakeRoot(kx);//创建一个根节点,这里的ptr赋值，并不能给root赋值
		return true;                   //加个引用就可以了。
	}*/
	//否则
	BstNode* pa = NULL;
	BstNode* p = ptr;  
	==================  要插入的值和树中的的值相同
	while (p != NULL &&  p->key != kx)
		{
		    pa = p;  //用来保存双亲结点
			if (kx < pa->key) p = pa->leftNode;
			else p = pa->rightNode;
			
		}
	//现在p的指向为空或者要插入的值和树中的的值相同，直接退出
		if (p != NULL && p->key == kx) return false;  
		================== 如果p为空，或者kx值在树中不存在
		p = BuyNode();
		p->key = kx;
		p->parent = pa;
		====================  如果为空没有根节点。则走下面
		if (ptr == NULL) //先判定 ptr是否为空，如果为空
		{    //p成为根节点
			ptr = p;//创建一个根节点,这里的ptr赋值，并不能给root赋值
		               //加个引用就可以了。
		}
		else
		{
			if (p->key < pa->key)pa->leftNode = p;
			else pa->rightNode = p;
			return true;
		}
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

void InOrder(BstNode *ptr)
{
	if (ptr != nullptr)
	{
		InOrder(ptr->leftNode);
		cout << ptr->key << " ";
		InOrder(ptr->rightNode);
	}
}
1
2
3
4
5
6
7
8
9

找到二叉排序树的最左边结点，则是最小的**

BstNode* First(BstNode* ptr)
{
	while (ptr != NULL && ptr->leftNode != NULL)
	{
		ptr = ptr->leftNode;
	}
	return ptr;
}
1
2
3
4
5
6
7
8

找最小结点的下一个节点。**

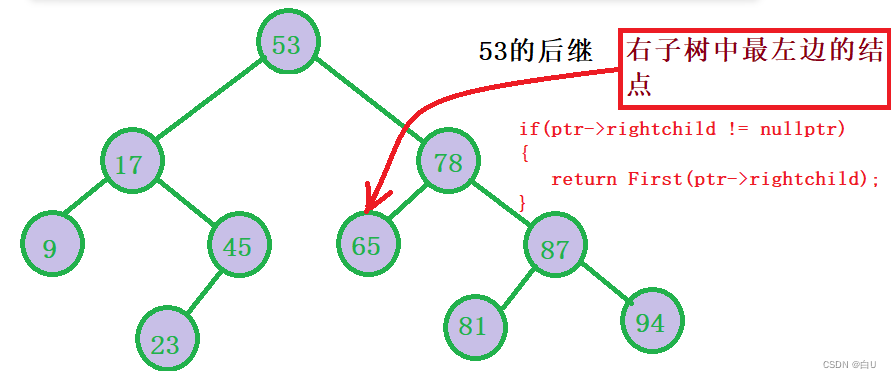
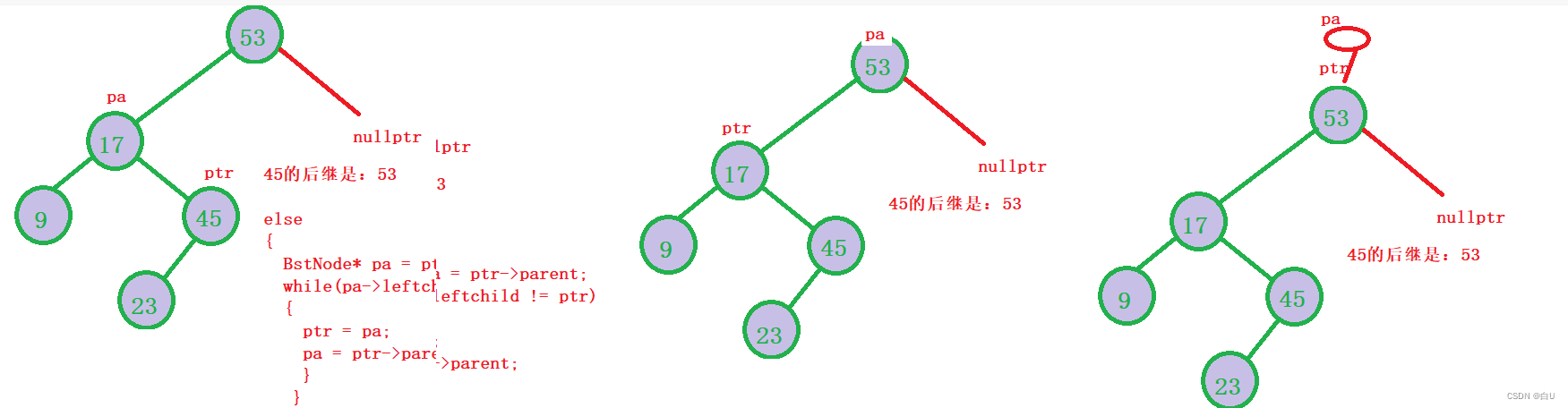
BstNode* Next(BstNode* ptr)
{
	if (ptr == NULL) return NULL;
	if (ptr->rightNode != NULL)
	{
		return First(ptr->rightNode);//找到最左边的数
	}
	else
	{ //核心代码
		BstNode* pa = ptr->parent;
		while (pa != NULL && pa->leftNode != ptr)
		{
			ptr = pa;
			pa = ptr->parent;
		}
		return pa;  //中序遍历的最左边结点的后继
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

//

void NiceOreder(BstNode* ptr)
{
	for (BstNode* p = First(ptr); p != NULL; p = Next(p))
	{
		cout << p->key << " ";
	}
	cout << endl;
	}
1
2
3
4
5
6
7
8

找最后一个结点

//找最后一个节点
BstNode* last(BstNode* ptr)
{
	while (ptr != NULL && ptr->rightNode != NULL)
	{
		ptr = ptr->rightNode;
	}
	return ptr;
}
1
2
3
4
5
6
7
8
9

找前驱

//找前驱
BstNode* Pre(BstNode* ptr)
{
	if (ptr == NULL) return NULL;
	if (ptr->leftNode != NULL)
	{
		return last(ptr->leftNode);//找到最左边的数
	}
	else
	{
		BstNode* pa = ptr->parent;
		while (pa != NULL && pa->rightNode != ptr)
		{
			ptr = pa;
			pa = ptr->parent;
		}
		return pa;  //中序遍历的最左边结点的后继
	}

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

//倒叙
void RevNiceOreder(BstNode* ptr)
{
	for (BstNode* p = last(ptr); p != NULL; p = Pre(p))
	{
		cout << p->key << " ";
	}
	cout << endl;
}
int main()
{
	BSTree root = NULL;
	int ar[] = { 53,17,78,9,45,65,87,23,81,94,88,100 };
	int n = sizeof(ar) / sizeof(ar[0]);
	for (int i = 0; i < n; ++i)
	{
		cout << Insert(root, ar[i]) << endl;;
	}
	InOrder(root);
	cout << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21