美赛 5：评价类模型、插值与拟合模型（十大模型篇）_美赛中用于评价的模型有哪些

目录

一、评价类模型

1.AHP（层次分析法）

2.TOPSIS法（优劣解距离方法）

二、插值与拟合模型

1.插值算法

2.拟合算法（cftool工具箱）

---

一、评价类模型

1.AHP（层次分析法）

        最基础的评价类模型，通过打分解决评价类问题（两两比较，推算权重）。

 

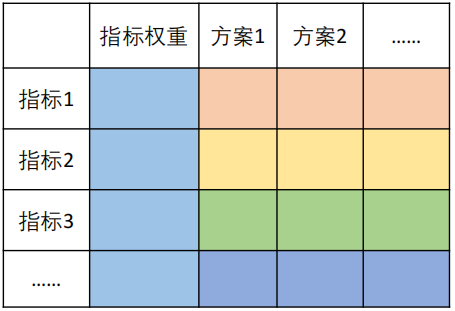
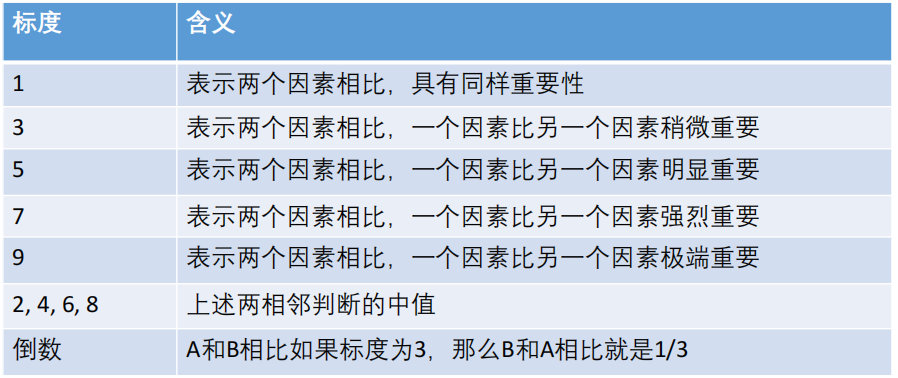
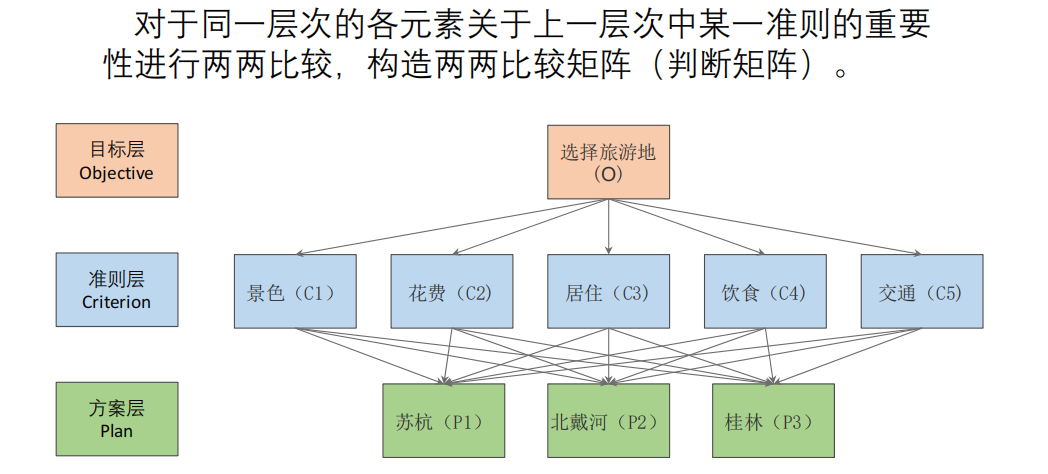
 Matlab代码：

disp('请输入判断矩阵A')
A=input('A=');
[n,n] = size(A);
 
% 方法1：算术平均法求权重
Sum_A = sum(A);
SUM_A = repmat(Sum_A,n,1);
Stand_A = A ./ SUM_A;
disp('算术平均法求权重的结果为：');
disp(sum(Stand_A,2)./n)
 
% 方法2：几何平均法求权重
Prduct_A = prod(A,2);
Prduct_n_A = Prduct_A .^ (1/n);
disp('几何平均法求权重的结果为：');
disp(Prduct_n_A ./ sum(Prduct_n_A))
 
% 方法3：特征值法求权重
[V,D] = eig(A);
Max_eig = max(max(D));
[r,c]=find(D == Max_eig , 1);
disp('特征值法求权重的结果为：');
disp( V(:,c) ./ sum(V(:,c)) )
 
% 计算一致性比例CR
CI = (Max_eig - n) / (n-1);
RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
 
if CR<0.10
    disp('因为CR<0.10，所以该判断矩阵A的一致性可以接受!');
else
    disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
end

 

---

2.TOPSIS法（优劣解距离方法）

        一种常用的综合评价方法，能充分利用原始数据的信息，反映各评价方案之间的差距。

改进：带权重的Topsis法（AHP or 熵权法）

Matlab代码：

load data_water_quality.mat
 
% 指标正向化
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标']) 
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理，需要请输入1 ，不需要输入0：  ']);
 
if Judge == 1
    Position = input('请输入需要正向化处理的指标所在的列，例如第2、3、6三列需要处理，那么你需要输入[2,3,6]： '); %[2,3,4]
    disp('请输入需要处理的这些列的指标类型（1：极小型， 2：中间型， 3：区间型） ')
    Type = input('例如：第2列是极小型，第3列是区间型，第6列是中间型，就输入[1,3,2]：  '); %[2,1,3]
 
    for i = 1 : size(Position,2)  
        X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));
    end
    disp('正向化后的矩阵 X =  ')
    disp(X)
end
 
% 矩阵标准化
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)
 
% 是否需要增加权重
disp("请输入是否需要增加权重向量，需要输入1，不需要输入0")
Judge = input('请输入是否需要增加权重： ');
if Judge == 1
    Judge = input('使用熵权法确定权重请输入1，否则输入0： ');
    if Judge == 1
        if sum(sum(Z<0)) >0  
            disp('原来标准化得到的Z矩阵中存在负数，所以需要对X重新标准化')
            for i = 1:n
                for j = 1:m
                    Z(i,j) = [X(i,j) - min(X(:,j))] / [max(X(:,j)) - min(X(:,j))];
                end
            end
            disp('X重新进行标准化得到的标准化矩阵Z为:  ')
            disp(Z)
        end
        weight = Entropy_Method(Z);
        disp('熵权法确定的权重为：')
        disp(weight)
    else
        disp(['如果你有3个指标，你就需要输入3个权重，例如它们分别为0.25,0.25,0.5, 则你需要输入[0.25,0.25,0.5]']);
        weight = input(['你需要输入' num2str(m) '个权数。' '请以行向量的形式输入这' num2str(m) '个权重: ']);
        OK = 0;  
        while OK == 0 
            if abs(sum(weight) -1)<0.000001 && size(weight,1) == 1 && size(weight,2) == m  
                OK =1;
            else
                weight = input('你输入的有误，请重新输入权重行向量: ');
            end
        end
    end
else
    weight = ones(1,m) ./ m ; %如果不需要加权重就默认权重都相同，即都为1/m
end
 
 
% 计算与最大值的距离和最小值的距离，并算出得分
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ] .* repmat(weight,n,1) ,2) .^ 0.5;   
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ] .* repmat(weight,n,1) ,2) .^ 0.5;  
S = D_N ./ (D_P+D_N);   
disp('最后的得分为：')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')

---

二、插值与拟合模型

1.插值算法

        数学建模中，常常需要根据已知的函数点进行数据、模型的处理和分析，而有时候现有的数据是极少的，不足以支撑分析的进行，这时就需要使用一些数学的方法，“模拟产生”一些新的但又比较靠谱的值来满足需求，这就是插值的作用。

分段三次埃尔米特插值 & 三次样条插值

Matlab代码：

% 在同一个脚本文件里面，要想画多个图，需要给每个图编号，否则只会显示最后一个图
 
% plot函数用法:
% plot(x1,y1,x2,y2) 
% 线方式： - 实线 :点线 -. 虚点线 - - 波折线 
% 点方式： . 圆点  +加号  * 星号  x x形  o 小圆
% 颜色： y黄； r红； g绿； b蓝； w白； k黑； m紫； c青

x = -pi:pi; 
y = sin(x); 
new_x = -pi:0.1:pi;
 
% 分段三次埃尔米特插值
p1 = pchip(x,y,new_x); 
 
% 三次样条插值
p2 = spline(x,y,new_x); 
 
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')
legend('样本点','分段三次埃尔米特插值','三次样条插值','Location','SouthEast') 

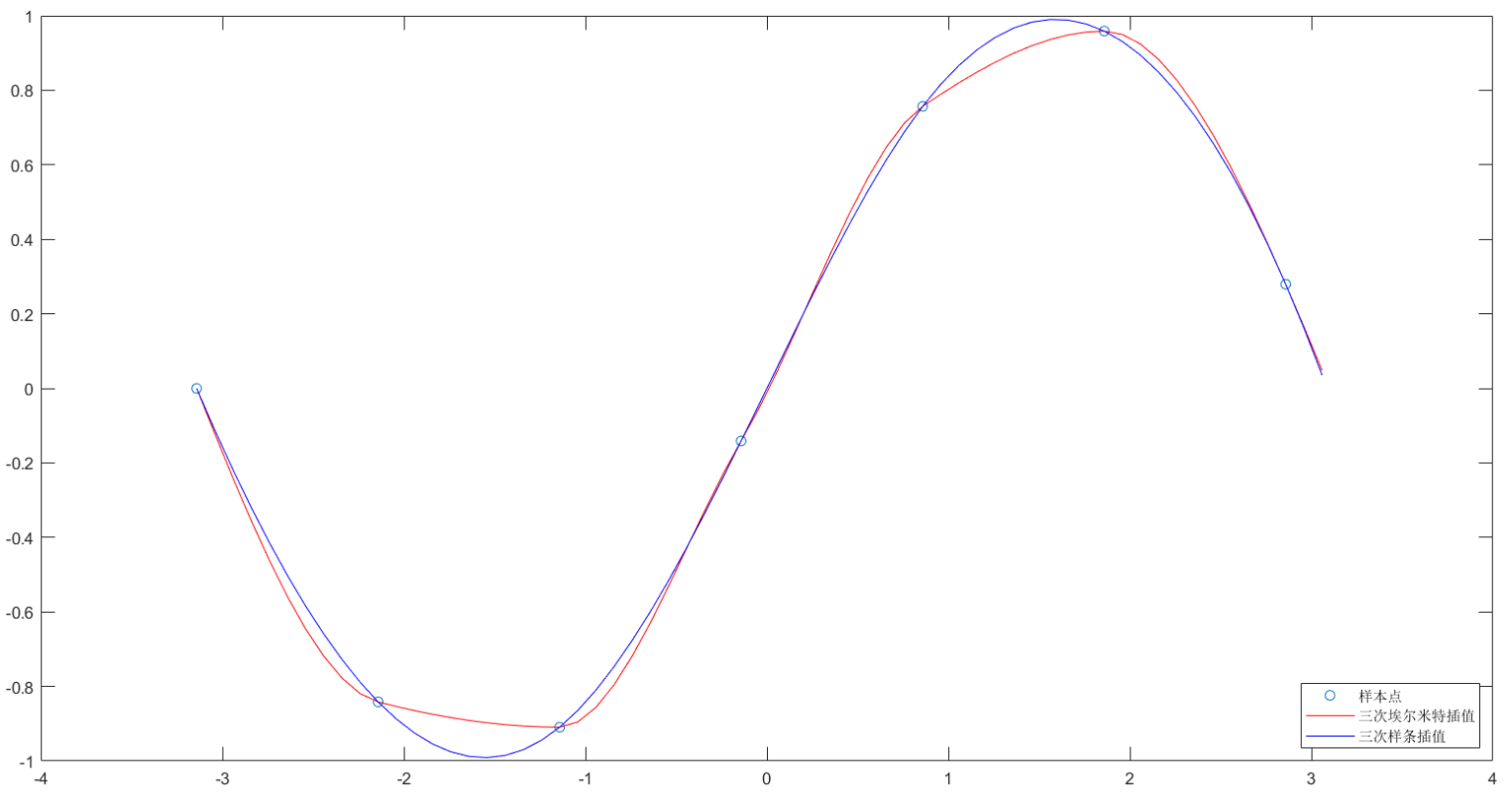
总结：三次样条插值生成的曲线更加光滑。在实际建模中，由于我们不知道数据的生成过程，因此两种插值方法都可以使用。

一个Excel 数据插值实例

 

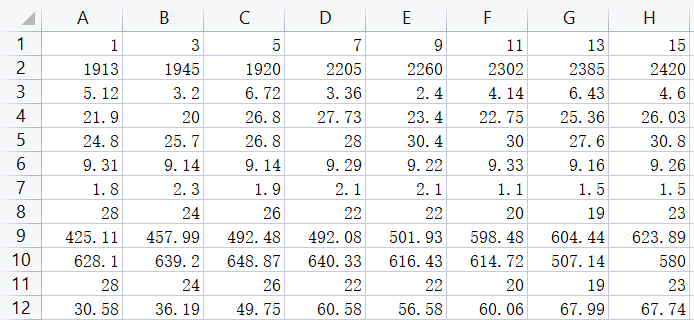
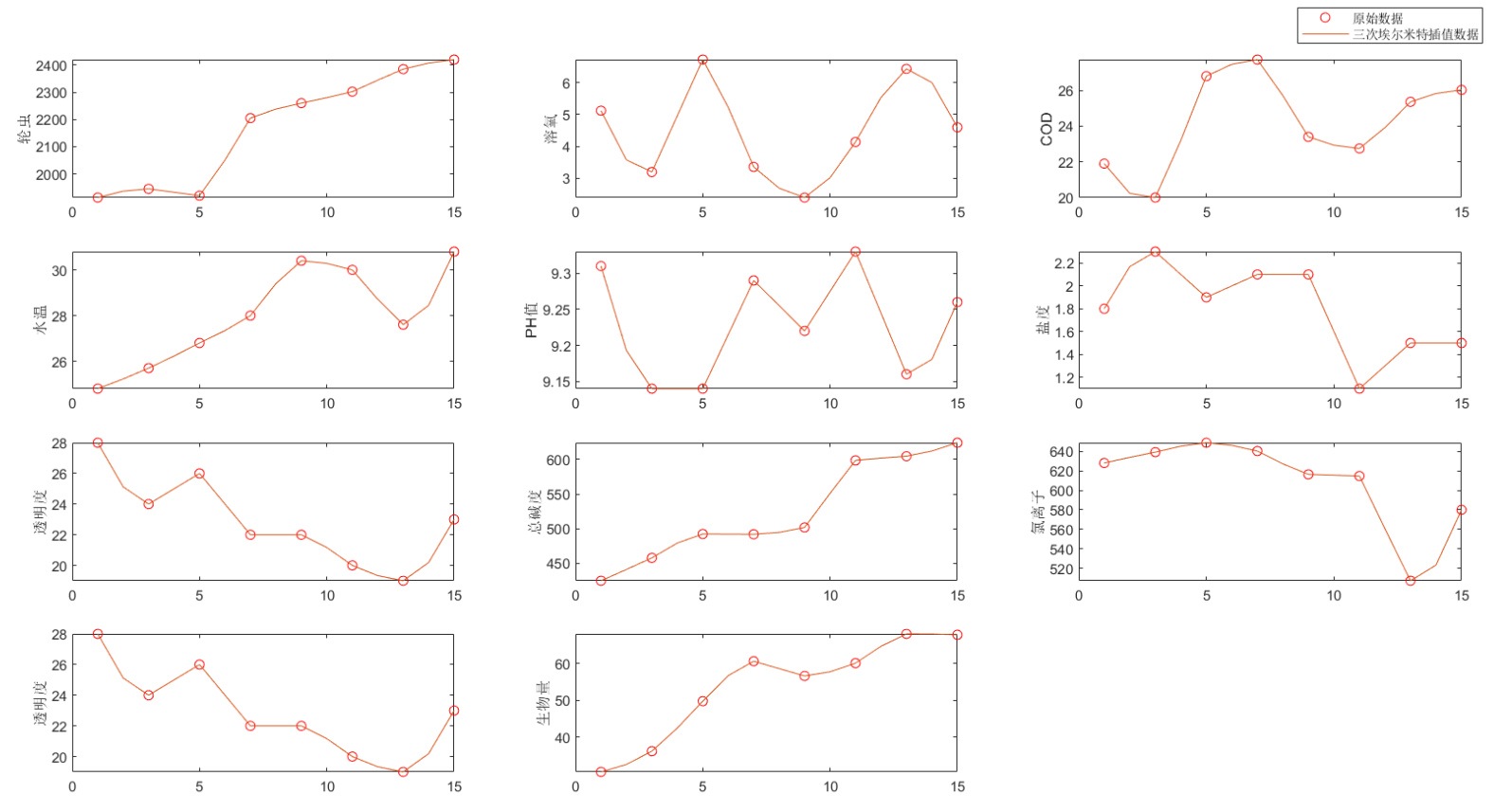
Matlab代码：

%% 插值预测中间周的水体评价指标
 
load Z.mat
x=Z(1,:);
[n,m]=size(Z);
 
% 注意Matlab的数组中不能保存字符串，如果要生成字符串数组，就需要使用元胞数组，用大括号{}定义和引用
ylab={'周数','轮虫','溶氧','COD','水温','PH值','盐度','透明度','总碱度','氯离子','透明度','生物量'};
disp(['共有' num2str(n-1) '个指标要进行插值。'])
 
P=zeros(11,15);
 
for i=2:n
    y=Z(i,:);
    new_x=1:15;
    p1=pchip(x,y,new_x);
    subplot(4,3,i-1);
    plot(x,y,'ro',new_x,p1,'-');
    axis([0 15,-inf,inf])
    %  xlabel('星期')
    ylabel(ylab{i})
    P(i-1,:)=p1;    
end
 
legend('原始数据','三次埃尔米特插值数据','Location','SouthEast')
 
%把P的第一行加上周数
P = [1:15; P]  

 

---

2.拟合算法（cftool工具箱）

        与插值问题不同，在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数（曲线），使得该曲线在某种准则下与所有的数据点最为接近，即曲线拟合的最好（最小化损失函数）。

 

Matlab代码：

load  data1
plot(x,y,'o')
 
xlabel('x的值')
ylabel('y的值')
n = size(x,1);
k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))
 
% 继续在之前的图形上来画图形
hold on 
% 显示网格线
grid on 
 
f=@(x) k*x+b;
fplot(f,[2.5,7]);
legend('样本数据','拟合函数','location','SouthEast')
 
% y的拟合值
y_hat = k*x+b; 
 
% 回归平方和
SSR = sum((y_hat-mean(y)).^2)  
 
% 误差平方和
SSE = sum((y_hat-y).^2) 
 
% 总体平方和
SST = sum((y-mean(y)).^2) 
 
% 拟合优度
R_2 = SSR / SST

 

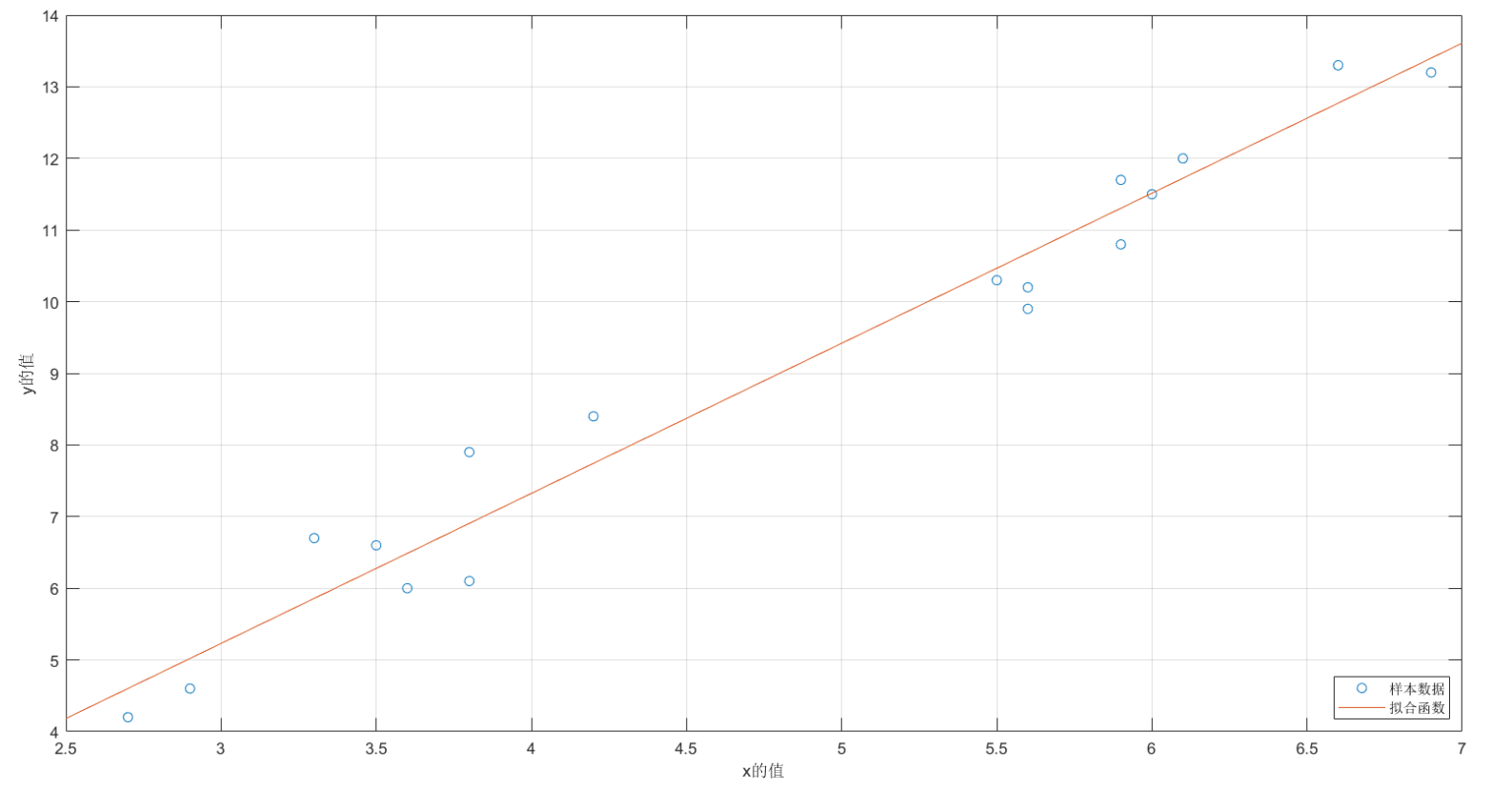
强大的曲线拟合工具箱：cftool

 注意调整 Fit Options 参数的起始点！

（导出图像可以在渲染设置中调整为高分辨率）

Matlab代码：

x = rand(30,1) * 10;
y = 3 * exp(0.5*x) -5 + normrnd(0,1,30,1);
% cftool 

---

内容原作者：数学建模清风

学习用途，仅作参考。