Beam Search解码_beam解码

Beam Search（束搜索）是一种在搜索空间中寻找最优解的算法。它常用于自然语言处理任务中，如机器翻译和语言生成。Beam Search通过在每个时间步选择概率最高的一组候选解来进行搜索，以此来寻找最有可能的解。

Beam Search的原理如下：

（1）首先，根据模型的输出概率分布，选择概率最高的K个候选解作为初始解集。

（2）在每个时间步，对于每个候选解，根据模型的输出概率分布，生成K个新的候选解。

（3）对于生成的新候选解，根据其得分（通常是概率的对数）进行排序，并选择得分最高的K个候选解作为下一步的候选解集。

（4）重复步骤2和步骤3，直到达到指定的搜索深度或满足终止条件为止。

（5）最后，从最终的候选解集中选择得分最高的解作为最终的输出。

1、数据准备

# 生成一个数组，在这个数组中寻求最优解。其中每一行代表着一个时刻。
#  t1   data00  data01  data02  data03  data04  data05
#  t2   data10  data11  data12  data13  data14  data15
#       ......  ......  ......  ......  ......  ......
#  tn   datan0  datan1  datan2  datan3  datan4  datan5
np.random.seed(1111)
data_origin = np.random.random([20, 6])
print("生成原始数据 data_origin : \n", data_origin, "\n")
 
# 模拟计算每个时刻的概率值
def softmax(logits):
    # 假设logits维度为：m*n
    # max_value是求得每一行的最大值,是一个m*1的数组
    max_value = np.max(logits, axis=1, keepdims=True)
    # exp的维度为：m*n
    exp = np.exp(logits - max_value)
    # exp_sum的维度为：m*1
    exp_sum = np.sum(exp, axis=1, keepdims=True)
    # dist的维度为：m*n
    dist = exp / exp_sum
    return dist
 
data_log = softmax(data_origin)
print("原始数据的概率 data_log : \n", data_log, "\n")

结果为：

生成原始数据 data_origin : 
 [[0.0955492  0.9250037  0.34357342 0.31047694 0.00200984 0.23559472]
 [0.23779172 0.73591587 0.49546808 0.78442535 0.12650631 0.60664932]
 [0.46612097 0.23713212 0.43515918 0.24367151 0.38383991 0.83839369]
 [0.65518473 0.14844667 0.63914517 0.63737456 0.61087429 0.93001855]
 [0.81649992 0.76942493 0.08540093 0.66500273 0.71169585 0.88733419]
 [0.26800864 0.24307673 0.7893055  0.37798441 0.79447948 0.86733103]
 [0.79581463 0.91718092 0.27112277 0.76085495 0.63041107 0.07933233]
 [0.13085797 0.30031675 0.32228152 0.16112149 0.31519324 0.52552848]
 [0.64584938 0.75064547 0.05602729 0.87420587 0.35373503 0.80443069]
 [0.06895161 0.17132584 0.12733474 0.45520635 0.62634312 0.00899385]
 [0.27226354 0.23227754 0.96010383 0.92113492 0.99903243 0.5457968 ]
 [0.24133854 0.14059083 0.63565862 0.90564256 0.61679546 0.8036375 ]
 [0.99099401 0.38455772 0.48742394 0.00766609 0.56447557 0.47900091]
 [0.39117119 0.01299563 0.04977387 0.48996132 0.50718393 0.37742878]
 [0.21948261 0.76436243 0.60285625 0.69879507 0.16387843 0.95983512]
 [0.94478792 0.18832797 0.42354165 0.06001482 0.29266343 0.37617702]
 [0.19016842 0.26495532 0.61076973 0.78200893 0.01128725 0.60054146]
 [0.79762971 0.88663537 0.43738937 0.73174125 0.77715349 0.29868446]
 [0.39374269 0.37934963 0.49425629 0.83092538 0.11742423 0.15918496]
 [0.57850174 0.27645561 0.6318197  0.99729503 0.79025817 0.17842424]] 
 
原始数据的概率 data_log : 
 [[0.12699445 0.29107993 0.16274224 0.15744421 0.11565412 0.14608504]
 [0.12487911 0.20550499 0.16158357 0.21571968 0.11172726 0.18058539]
 [0.16842255 0.13395275 0.16328779 0.13483159 0.15511937 0.24438595]
 [0.17117829 0.10312766 0.16845457 0.16815657 0.1637589  0.22532402]
 [0.18979942 0.18107165 0.09136558 0.16311747 0.17091455 0.20373132]
 [0.12063207 0.11766167 0.20316979 0.13465568 0.20422371 0.21965708]
 [0.19910643 0.2247988  0.11781878 0.192266   0.16875297 0.09725702]
 [0.14059406 0.16655666 0.17025551 0.14491397 0.16905296 0.20862685]
 [0.17123365 0.19015226 0.09493637 0.21516076 0.12785728 0.20065967]
 [0.13647602 0.15118786 0.1446811  0.20081893 0.23830239 0.1285337 ]
 [0.10814803 0.10390894 0.21515125 0.2069283  0.22369195 0.14217152]
 [0.11708187 0.10586087 0.17367634 0.22750618 0.17043097 0.20544377]
 [0.26484441 0.14441719 0.1600638  0.09906881 0.17288456 0.15872124]
 [0.17828226 0.122143   0.12671883 0.19679413 0.20021279 0.17584899]
 [0.11300484 0.19486567 0.16580365 0.1824987  0.1068928  0.23693435]
 [0.28064958 0.13171584 0.16664413 0.11585435 0.146201   0.1589351 ]
 [0.12900848 0.13902657 0.19646405 0.23315854 0.10787757 0.1944648 ]
 [0.1881916  0.20570976 0.13126527 0.17619161 0.18437733 0.11426443]
 [0.16156969 0.15926087 0.17865386 0.25016465 0.12256214 0.1277888 ]
 [0.16076369 0.11885323 0.16956791 0.24438108 0.1986793  0.10775478]] 

2、举例说明

假设现在有一个简化版的中文翻译英文任务，输入和输出如下，为了方便描述搜索算法，限制输出词典只有{"W", "A", "Z", "G"} 这4个候选词，限制1个时间步长翻译1个汉字，1个汉字对应1个英文单词，这里总共4个汉字，所以只有4个时间步长。

中文输入："我" "爱" "中" "国"

英文输出："W" "A" "Z" "G"

目标：得到最优的翻译序列 W-A-Z-G

3、exhaustive search（穷举搜索）

最直观的方法就是穷举所有可能的输出序列，4个时间步长，每个步长4种选择，共计4*4=36 种排列组合。从所有的排列组合中找到输出条件概率最大的序列。穷举搜索能保证全局最优，但计算复杂度太高，当输出词典稍微大一点根本无法使用。

4、Greedy Search（贪心搜索）

贪心算法在翻译每个字的时候，直接选择条件概率最大的候选值作为当前最优。如下图所以：

第1个时间步长：首先翻译"我"，发现候选"W"的条件概率最大为0.6，所以第一个步长直接翻译成了"W"。

第2个时间步长：翻译"我爱"，发现WW概率0.2，WA概率0.6，WZ概率0.1，WG概率0.1，所以选择WA作为当前步长最优翻译结果。

第3个时间步长：翻译"我爱中"，发现WAW概率0.05，WAA概率0.05，WAZ概率0.8，WAG概率0.1，所以选择WAZ作为最终的翻译结果。

第4个时间步长：翻译"我爱中国"，发现WAZW概率0.05，WAZA概率0.05，WAZZ概率0.1，WAZG概率0.8，所以选择WAZG作为最终的翻译结果。

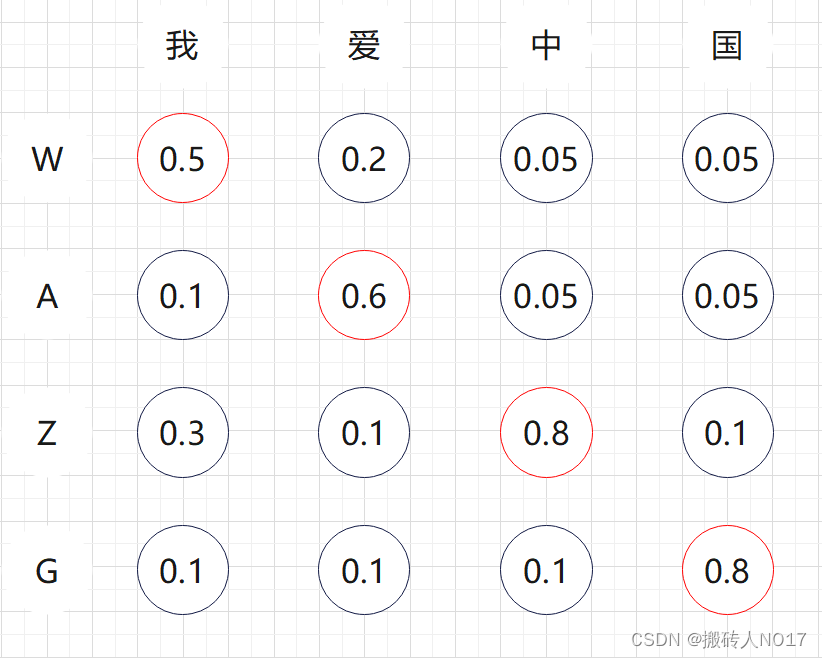
贪心算法每一步选择中都采取在当前状态下最好或最优的选择，通过这种局部最优策略期望产生全局最优解。但是期望是好的，能不能实现是另外一回事了。贪心算法本质上没有从整体最优上加以考虑，并不能保证最终的结果一定是全局最优的。但是相对穷举搜索，搜索效率大大提升。

5、Beam Search（束搜索）

Beam Search是对Greedy Search的一个改进算法。相对Greedy Search扩大了搜索空间，但远远不及穷举搜索指数级的搜索空间，是二者的一个折中方案。

Beam Search有一个超参数beam size（束宽），设为 K。第一个时间步长，选取当前条件概率最大的 K个词，当做候选输出序列的第一个词。之后的每个时间步长，基于上个步长的输出序列，挑选出所有组合中条件概率最大的 K 个，作为该时间步长下的候选输出序列。始终保持 K 个候选。最后从 K个候选中挑出最优的。

还是以上面的任务为例，假设 K=2 ，我们走一遍这个搜索流程。

1、第一个时间步长：如下图所示，W和Z的概率是top2，所以第一个时间步长的输出的候选是W和Z，将W和Z加入到候选输出序列中。

2、第2个时间步长：如下图所示，以W开头有四种候选{WW, WA, WA, WG}，以Z开头有四种候选{ZW, ZA, ZZ, ZG}。从这8个候选中挑出条件概率最大的2个，即WA和ZA，作为候选输出序列。

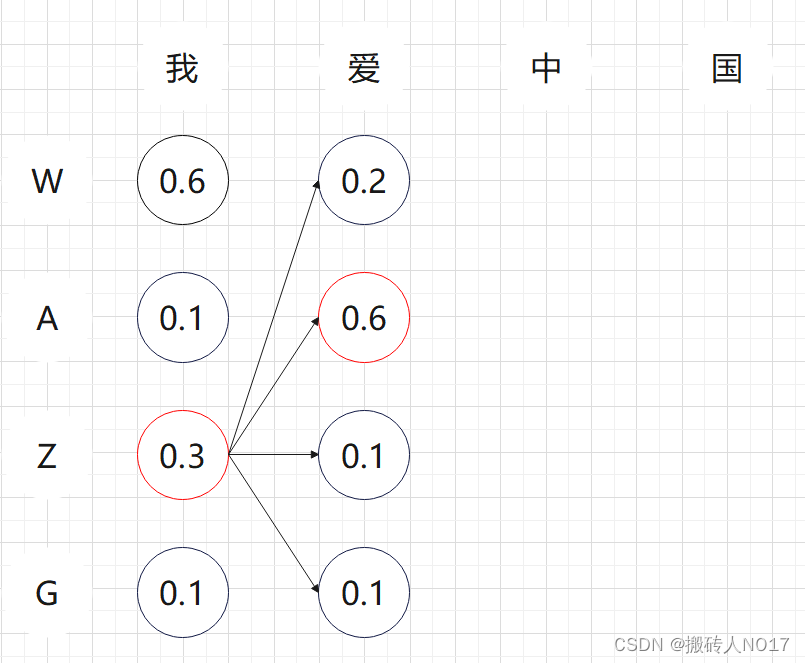
3、第3个时间步长：同理，以WA开头有四种候选{WAW, WAA, WAZ, WAG}，以ZA开头有四种候选{ZAW, ZAA, ZAZ, ZAG}。从这8个候选中挑出条件概率最大的2个，即WAZ和WAG，作为候选输出序列。

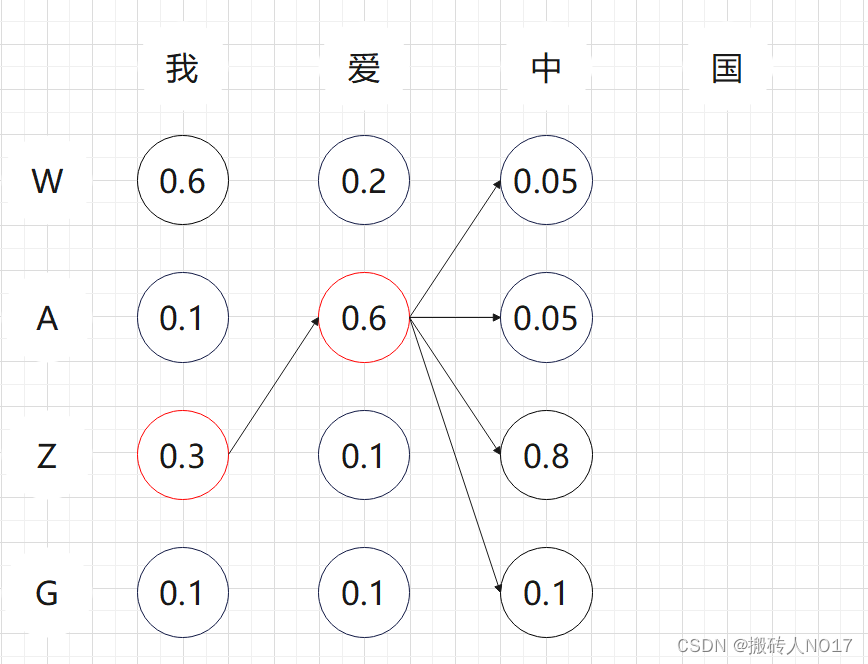
4、第4个时间步长：同理，以WAZ开头有四种候选{WAZW, WAZA, WAZZ, WAZG}，以ZAG开头有四种候选{ZAGW, ZAGA, ZAGZ, ZAGG}。从这8个候选中挑出条件概率最大的2个，即WAZZ和WAZG，作为候选输出序列。因为4个步长就结束了，直接从WAZG和WAZZ中挑选出最优值WAZG作为最终的输出序列。

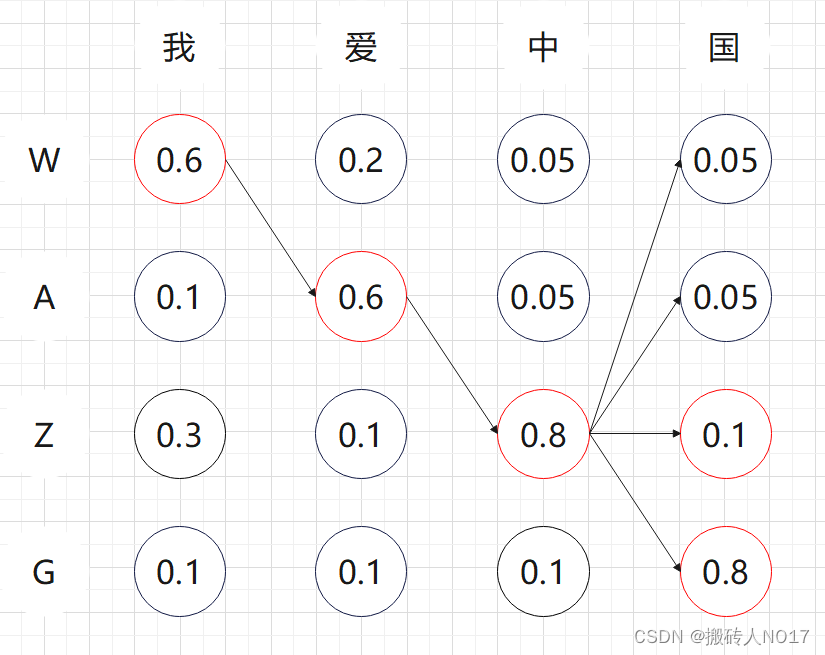
5、beam search不保证全局最优，但是比greedy search搜索空间更大，一般结果比greedy search要好。

6、greedy search 可以看做是 beam size = 1时的 beam search。

6、Prefix Beam Search（前缀束搜索）

参考论文：First-Pass Large Vocabulary Continuous Speech Recognition using Bi-Directional Recurrent DNNs.

有许多不同的路径在many-to-one map的过程中是相同的，但Beam Search却会将一部分舍去，这导致了很多有用的信息被舍弃了。比如许多单个概率低，但是合在一起概率就很高的情况。这种想法就催生了Prefix Beam Search。基本的思想是将记录prefix的时候不在记录raw sequence，而是记录去掉blank和duplicate的sequence（具体步骤较复杂，会同时保留duplicate的序列和没duplicate的序列）。

前缀束搜索（Prefix Beam Search）方法，可以在搜索过程中不断的合并相同的前缀。具体较复杂，不过读者弄懂Beam Search后再想想Prefix Beam Search的流程不是很难，主要弄懂probability With Blank和probability No Blank分别代表最后一个字符是空格和最后一个字符不是空格的概率即可。

理解：

令*表示任意字符串（经过many-to-one map后的），比如，这里的-表示Blank。如果*表示的字符串的尾部是Blank则*表示为，即。同理。

那么任意字符串*与一个新的字符结合有多少种情况呢？一共有这样5种情况（为了简便，令*最后一个字符为A）：

（1）

（2）

（3）

（4）

（5）

7、代码

import numpy as np
from math import log
from collections import defaultdict
 
# 生成一个数组，在这个数组中寻求最优解。其中每一行代表着一个时刻。
#  t1   data00  data01  data02  data03  data04  data05
#  t2   data10  data11  data12  data13  data14  data15
#       ......  ......  ......  ......  ......  ......
#  tn   datan0  datan1  datan2  datan3  datan4  datan5
np.random.seed(1111)
data_origin = np.random.random([20, 6])
print("生成原始数据 data_origin : \n", data_origin, "\n")
 
# 模拟计算每个时刻的概率值
def softmax(logits):
    # 假设logits维度为：m*n
    # max_value是求得每一行的最大值,是一个m*1的数组
    max_value = np.max(logits, axis=1, keepdims=True)
    # exp的维度为：m*n
    exp = np.exp(logits - max_value)
    # exp_sum的维度为：m*1
    exp_sum = np.sum(exp, axis=1, keepdims=True)
    # dist的维度为：m*n
    dist = exp / exp_sum
    return dist
 
data_log = softmax(data_origin)
print("原始数据的概率 data_log : \n", data_log, "\n")
 
 
# 去除空格【规定了blank字符是"0"】
def remove_blank(labels, blank=0):
    new_labels = []
    # 合并重复字符
    previous = None
    for l in labels:
        if l != previous:
            new_labels.append(l)
            previous = l
    # 去除重复字符
    new_labels = [l for l in new_labels if l != blank]
    return new_labels
 
# 插入空格
def insert_blank(labels, blank=0):
    new_labels = [blank]
    for l in labels:
        new_labels += [l, blank]
    return new_labels
 
# Greedy Search操作
def greedy_decode(data, blank=0):
    # 得到data中每一行的最大值的下标【每一行代表着一个时刻，有多少行就有多少时刻】
    raw_rs = np.argmax(data, axis=1)
    rs = remove_blank(raw_rs, blank)
    return raw_rs, rs
 
# 使用Greedy Search解码
rr, rs = greedy_decode(data_log)
print("使用Greedy Search未删除blank时的结果为：", rr)
print("使用Greedy Search已删除blank时的结果为：", rs)
 
# 使用Beam Search【束搜索】解码
def beam_decode(data, beam_size=10):
    # data是个二维数组，记录了所有时刻的所有元素的概率
    T, V = data.shape     # T是时刻，V是每一个时刻的维度
    # 将所有的data中值改为log是为了防止溢出，因为最后得到的p是data1...datan连乘，且datai都在0到1之间，可能会导致下溢出
    # 改成log(data)以后就变成连加了，这样就防止了下溢出
    log_y = np.log(data)
    # 初始的beam为一个tuple组成的list；tuple是由一个list【prefix】和一个概率【log】值组成。
    beam = [([], 0)]
    # 遍历所有时刻t
    for t in range(T):
        # 在每个时刻，都先初始化一个new_beam为一个空的list
        new_beam = []
        # 遍历上一次查询的结果beam, prefix是查找过的字符串, score是查找过的字符串的得分
        for prefix, score in beam:
            # 遍历这一个时刻中的每一个元素的概率值(一共V项)
            for i in range(V):
                # 记录添加的新项是这个时刻的第几项，对应的概率(log形式的)加上新的这项log形式的概率(本来是乘的，改成log就是加)
                new_prefix = prefix + [i]        # 往下遍历的过程中，向prefix中添加新元素的位置信息【即prefix+[]】
                new_score = score + log_y[t, i]  # 往下遍历的过程中，向log中添加新元素的概率值【score+log_y[t,i]】
                # new_beam记录了beam中现有的每一个prefix加上新时刻的每个元素和概率，然后组成新的候选项，再从其中选出beam_size个
                new_beam.append((new_prefix, new_score))
        # 给new_beam按score排序
        new_beam.sort(key=lambda x: x[1], reverse=True)
        # beam即为new_beam中概率最大的beam_size个路径
        beam = new_beam[:beam_size]
    return beam
 
beam_chosen = beam_decode(data_log, beam_size=100)
print("Beam Search(束搜索)的前20条结果： ")
for beam_string, beam_score in beam_chosen[:20]:
    print(remove_blank(beam_string), beam_score)
 
 
# Prefix Beam Search代码实现
ninf = float("-inf")     # python中的最小值
 
def _logsumexp(a, b):
    # np.log(np.exp(a) + np.exp(b))
    if a < b:
        a, b = b, a
    if b == ninf:
        return a
    else:
        return a + np.log(1 + np.exp(b - a))
 
def logsumexp(*args):
    # from scipy.special import logsumexp
    # logsumexp(args)
    res = args[0]
    for e in args[1:]:
        res = _logsumexp(res, e)
    return res
 
def prefix_beam_decode(y, beam_size=10, blank=0):
    """
    对给定输出概率进行预测
    Arguments:
        y: 输出概率 (e.g. post-softmax) for each time step. Should be an array of shape (time x output dim).
        beam_size (int): Size of the beam to use during inference.
        blank (int): Index of the CTC blank label.
    Returns the output label sequence and the corresponding negative log-likelihood estimated by the decoder.
    """
    T, V = y.shape
    log_y = np.log(y)
 
    # 在beam中的元素为(prefix, (probability_blank, probability_no_blank))
    # 初始beam为空序列，第一个是前缀，第二个是后接blank的log概率，第三个是后接非blank的log概率
    # 我们需要后接blank和后接非blank两种情况，来区分重复字符是否应该被合并，对于后接blank的情况，重复字符就不会被合并
    beam = [(tuple(), (0, ninf))]
    # 沿时间维度循环，对于每一个时刻t
    for t in range(T):
        # 使用普通的字典时，用法一般是dict={},添加元素的只需要dict[element] =value即可，调用的时候也是如此
        # dict[element] = xxx,但前提是element不在字典里，如果不在字典里就会报错
        # defaultdict的作用是在于，当字典里的key不存在但被查找时，返回的不是keyError而是一个默认值
        # dict = defaultdict(factory_function)
        # 这个factory_function可以是list、set、str等等，作用是当key不存在时，返回的是工厂函数的默认值
        # 这里就是(ninf, ninf)是默认值
        # new_beam为存储下一个候选集的预设置字典，每次新的时间节点都会重设
        new_beam = defaultdict(lambda: (ninf, ninf))
        # 对于beam中的每一项
        for prefix, (p_b, p_nb) in beam:
            for i in range(V):
                # beam的每一项都加上时刻t中的每一项
                p = log_y[t, i]
                # 如果新元素项i的属性是blank，那么前缀不会改变，因为后接的是blank，所以只需要更新前缀不变的情况下后接blank的log概率
                # p=log_y[t,i]是新元素项的概率，使用logsumexp(new_p_b, p_b + p, p_nb + p)进行更新
                if i == blank:
                    # 将新元素项直接加入路径中，路径prefix不变【因为新元素项i的属性是blank】
                    new_p_b, new_p_nb = new_beam[prefix]
                    new_p_b = logsumexp(new_p_b, p_b + p, p_nb + p)
                    new_beam[prefix] = (new_p_b, new_p_nb)
                    continue
                # 如果新元素项的属性不是blank，那么需要考虑前缀prefix会不会改变的情况，
                # 记录前缀prefix的最后一个字符，用于判断当前字符与前缀最后一个字符是否相同
                end_t = prefix[-1] if prefix else None
                # 让前缀prefix加上新元素项i后，得到新的前缀new_prefix，判断new_prefix是否在上一轮的beam结果中【可能存在】
                new_prefix = prefix + (i,)                 # new_prefix代表next prefix
                new_p_b, new_p_nb = new_beam[new_prefix]   # new_p_b代表 next probability of blank
                if i != end_t:
                    # 如果新元素项i和prefix的最后一个字符不一样，则将新元素项i加入路径前缀prefix中，并将整体加入到beam中
                    # 因为后接的是非blank，所以只需要更新后接非blank的log概率【即只更新new_p_nb】
                    # 上一轮的结果中，有两种情况：1、最后一个不是blank；2、最后一个是blank。所以计算的时候都要考虑。
                    new_p_nb = logsumexp(new_p_nb, p_b + p, p_nb + p)
                else:
                    # 如果新元素项i和prefix的最后一个字符一样，那么我们在更新后接非blank的log概率时不包括上一时刻后接非blank的概率。
                    # --------CTC算法会合并没有用blank分隔的重复字符--------
                    new_p_nb = logsumexp(new_p_nb, p_b + p)
                # 如果新元素项i和prefix的最后一个字符一样，分两种情况添加：
                #     1、new_prefix=prefix+(i,)  添加新元素项i，则最后两个字符会重复，计算概率，添加到new_beam中，优选
                #     2、new_prefix=prefix       不添加新元素项i，prefix中没有重复字符，计算概率，添加到new_beam中，优选
                new_beam[new_prefix] = (new_p_b, new_p_nb)   # 这一步：new_prefix最后两个字符是一样的
                # 如果一样，保留现有的路径前缀prefix，但是概率上要加上新的这个元素项i的概率
                if i == end_t:
                    new_p_b, new_p_nb = new_beam[prefix]
                    new_p_nb = logsumexp(new_p_nb, p_nb + p)
                    new_beam[prefix] = (new_p_b, new_p_nb)
        # 给新的beam排序并取前beam_size个
        beam = sorted(new_beam.items(), key=lambda x: logsumexp(*x[1]), reverse=True)
        beam = beam[:beam_size]
    return beam
 
beam_test = prefix_beam_decode(data_log, beam_size=100)
print("Prefix Beam Search(束搜索)的前20条结果： ")
for beam_string, beam_score in beam_test[:20]:
    print(remove_blank(beam_string), beam_score)

结果：

生成原始数据 data_origin : 
 [[0.0955492  0.9250037  0.34357342 0.31047694 0.00200984 0.23559472]
 [0.23779172 0.73591587 0.49546808 0.78442535 0.12650631 0.60664932]
 [0.46612097 0.23713212 0.43515918 0.24367151 0.38383991 0.83839369]
 [0.65518473 0.14844667 0.63914517 0.63737456 0.61087429 0.93001855]
 [0.81649992 0.76942493 0.08540093 0.66500273 0.71169585 0.88733419]
 [0.26800864 0.24307673 0.7893055  0.37798441 0.79447948 0.86733103]
 [0.79581463 0.91718092 0.27112277 0.76085495 0.63041107 0.07933233]
 [0.13085797 0.30031675 0.32228152 0.16112149 0.31519324 0.52552848]
 [0.64584938 0.75064547 0.05602729 0.87420587 0.35373503 0.80443069]
 [0.06895161 0.17132584 0.12733474 0.45520635 0.62634312 0.00899385]
 [0.27226354 0.23227754 0.96010383 0.92113492 0.99903243 0.5457968 ]
 [0.24133854 0.14059083 0.63565862 0.90564256 0.61679546 0.8036375 ]
 [0.99099401 0.38455772 0.48742394 0.00766609 0.56447557 0.47900091]
 [0.39117119 0.01299563 0.04977387 0.48996132 0.50718393 0.37742878]
 [0.21948261 0.76436243 0.60285625 0.69879507 0.16387843 0.95983512]
 [0.94478792 0.18832797 0.42354165 0.06001482 0.29266343 0.37617702]
 [0.19016842 0.26495532 0.61076973 0.78200893 0.01128725 0.60054146]
 [0.79762971 0.88663537 0.43738937 0.73174125 0.77715349 0.29868446]
 [0.39374269 0.37934963 0.49425629 0.83092538 0.11742423 0.15918496]
 [0.57850174 0.27645561 0.6318197  0.99729503 0.79025817 0.17842424]] 
 
原始数据的概率 data_log : 
 [[0.12699445 0.29107993 0.16274224 0.15744421 0.11565412 0.14608504]
 [0.12487911 0.20550499 0.16158357 0.21571968 0.11172726 0.18058539]
 [0.16842255 0.13395275 0.16328779 0.13483159 0.15511937 0.24438595]
 [0.17117829 0.10312766 0.16845457 0.16815657 0.1637589  0.22532402]
 [0.18979942 0.18107165 0.09136558 0.16311747 0.17091455 0.20373132]
 [0.12063207 0.11766167 0.20316979 0.13465568 0.20422371 0.21965708]
 [0.19910643 0.2247988  0.11781878 0.192266   0.16875297 0.09725702]
 [0.14059406 0.16655666 0.17025551 0.14491397 0.16905296 0.20862685]
 [0.17123365 0.19015226 0.09493637 0.21516076 0.12785728 0.20065967]
 [0.13647602 0.15118786 0.1446811  0.20081893 0.23830239 0.1285337 ]
 [0.10814803 0.10390894 0.21515125 0.2069283  0.22369195 0.14217152]
 [0.11708187 0.10586087 0.17367634 0.22750618 0.17043097 0.20544377]
 [0.26484441 0.14441719 0.1600638  0.09906881 0.17288456 0.15872124]
 [0.17828226 0.122143   0.12671883 0.19679413 0.20021279 0.17584899]
 [0.11300484 0.19486567 0.16580365 0.1824987  0.1068928  0.23693435]
 [0.28064958 0.13171584 0.16664413 0.11585435 0.146201   0.1589351 ]
 [0.12900848 0.13902657 0.19646405 0.23315854 0.10787757 0.1944648 ]
 [0.1881916  0.20570976 0.13126527 0.17619161 0.18437733 0.11426443]
 [0.16156969 0.15926087 0.17865386 0.25016465 0.12256214 0.1277888 ]
 [0.16076369 0.11885323 0.16956791 0.24438108 0.1986793  0.10775478]] 
 
使用Greedy Search未删除blank时的结果为： [1 3 5 5 5 5 1 5 3 4 4 3 0 4 5 0 3 1 3 3]
使用Greedy Search已删除blank时的结果为： [1, 3, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3]
Beam Search(束搜索)的前20条结果： 
[1, 3, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.261797539205567
[1, 3, 5, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.279020152518033
[1, 3, 5, 1, 5, 3, 4, 2, 3, 4, 5, 3, 1, 3] -29.300726142201842
[1, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.310307014773972
[1, 3, 5, 1, 5, 3, 4, 2, 3, 3, 5, 3, 1, 3] -29.31794875551431
[1, 5, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.327529628086438
[1, 3, 5, 1, 5, 4, 3, 4, 5, 3, 1, 3] -29.331572723457334
[1, 3, 5, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.33263180992451
[1, 3, 5, 4, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.334649090836038
[1, 3, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.33969505198154
[1, 3, 5, 2, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.339823066915415
[1, 3, 5, 1, 5, 4, 3, 3, 5, 3, 1, 3] -29.3487953367698
[1, 5, 1, 5, 3, 4, 2, 3, 4, 5, 3, 1, 3] -29.349235617770248
[1, 3, 5, 5, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.349854423236977
[1, 3, 5, 1, 5, 3, 4, 3, 4, 5, 3, 3] -29.350803198551016
[1, 3, 5, 4, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.351871704148504
[1, 3, 5, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.356917665294006
[1, 3, 5, 2, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.35704568022788
[1, 3, 5, 1, 5, 3, 4, 5, 4, 5, 3, 1, 3] -29.363802591012263
[1, 5, 1, 5, 3, 4, 2, 3, 3, 5, 3, 1, 3] -29.366458231082714
Prefix Beam Search(束搜索)的前20条结果： 
[1, 5, 4, 1, 3, 4, 5, 2, 3] (-18.189863809114193, -17.613677981426175)
[1, 5, 4, 5, 3, 4, 5, 2, 3] (-18.19636512622969, -17.621013424585406)
[1, 5, 4, 1, 3, 4, 5, 1, 3] (-18.31701896033153, -17.666629973270073)
[1, 5, 4, 5, 3, 4, 5, 1, 3] (-18.323388267369936, -17.674125139073176)
[1, 5, 4, 1, 3, 4, 3, 2, 3] (-18.415808498759556, -17.862744326248826)
[1, 5, 4, 1, 3, 4, 3, 5, 3] (-18.36642276663863, -17.898463479112884)
[1, 5, 4, 5, 3, 4, 3, 2, 3] (-18.42224294936932, -17.870025672291458)
[1, 5, 4, 5, 3, 4, 3, 5, 3] (-18.37219911390019, -17.905130493229173)
[1, 5, 4, 1, 3, 4, 5, 4, 3] (-18.457066311773847, -17.880630315602037)
[1, 5, 4, 5, 3, 4, 5, 4, 3] (-18.462614293487096, -17.88759583852546)
[1, 5, 4, 1, 3, 4, 5, 3, 2] (-18.458941701567706, -17.951422824358747)
[1, 5, 4, 5, 3, 4, 5, 3, 2] (-18.464527031120184, -17.958629487208658)
[1, 5, 4, 1, 3, 4, 3, 1, 3] (-18.540857550725587, -17.92058991009369)
[1, 5, 4, 5, 3, 4, 3, 1, 3] (-18.547146092248852, -17.928030266681613)
[1, 5, 4, 1, 3, 4, 5, 3, 2, 3] (-19.325467801462263, -17.6892032244089)
[1, 5, 4, 5, 3, 4, 5, 3, 2, 3] (-19.328748799764973, -17.694105969982637)
[1, 5, 4, 1, 3, 4, 5, 3, 4] (-18.79699026165903, -17.945090229238392)
[1, 5, 4, 5, 3, 4, 5, 3, 4] (-18.80358553427324, -17.95258394264377)
[1, 5, 4, 3, 4, 3, 5, 2, 3] (-19.18153184608281, -17.859420073785095)
[1, 5, 4, 1, 3, 4, 5, 2, 3, 2] (-19.4393492963852, -17.884502168470895)
 
Process finished with exit code 0