机器学习：高斯朴素贝叶斯分类器(原理+python实现）_高斯贝叶斯分类python实现

一 原理

具体例子
我们通过判定花萼长度，花萼宽度，花瓣长度，花瓣宽度的尺寸大小来识别鸢尾花的类别。关于数据集，是通过sklean加载而来，这次只采用前一百个数据进行训练，使得花的类别只有0和1两个类别，因此我们这次目标是通过花的四个特征来判断类别是0还是1。

from sklearn.datasets import load_iris
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, :])
    print(data)
    return data[:,:-1], data[:,-1]
1
2
3
4
5
6
7
8
9

根据贝叶斯准则，可以得到在固定特征下，每个类别的概率，其表达式具体如下：

如果p(类别1│固定特征) > p(类别2│固定特征)，则在给出的特征下，类别属于1的概率大，因此预测类别为1，可以看出贝叶斯决策理论是通过计算概率，选择概率较大的来预测类别。
需要注意的是，p(固定特征│类别i)中的固定特征有4个，如果假设各个特征是相互独立的，则可以写成(之所以在贝叶斯前面加上朴素，正是这个独立性假设)：

• p(固定特征1│类别i)*p(固定特征2│类别i)*p(固定特征3│类别i)p(固定特征4│类别i)

那么针对p(固定特征1│类别1)而言，当选择高斯模型时，可以通过下述公式计算：

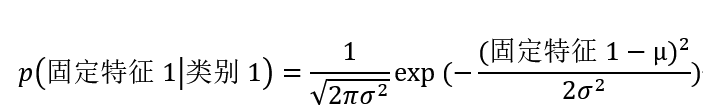
其中，σ^2和μ表示为方差和期望，是通过在类别1的训练样本里，计算出特征1的方差和期望，固定特征1表示为特征1的一个固定值，因此可以根据测试数据中一个数据的特征1的值来计算出该数据的p(固定特征1│类别1)。
看到这里，可能会想，为什么p(固定特征1│类别1)时， 为何要用高斯概率分布函数来计算概率呢？
这是因为数据集的特征都是属于连续型的特征，并非离散型，所以当给出一个具体的特征值的时候，是无法通过数据集来计算出该特征值的概率，此外，数据集的样本数一般也较少，无法将特征值划分到某个区间来计算概率。因此，当遇到这样的问题时，我们假设特征的分布是符合高斯分布，那么就可以通过该分布函数计算出任意特征值所对应的概率，所以p(固定特征1│类别1)的问题也就解决了。

二 代码实现逻辑

输入训练集数据
输入测试集数据
对于每一个类别i：
	对于每一个特征j：
		计算训练集的方差，期望
		根据测试集来计算p(固定特征j│类别i)
根据测试集来计算p_i=p(固定特征│类别i)* p(类别)
根据p_i相对大小，返回预测类别
计算分类正确率
1
2
3
4
5
6
7
8
9

三 代码示例

import numpy as np
import matplotlib.pyplot 
1