AtCoder Beginner Contest 332 G. Not Too Many Balls(最大流转最小割 dp)

题目

n(n<=500)种球，第i种有ai(0<=ai<=1e12)个球，

m(m<=5e5)个盒子，第j个能放bj(0<=bj<=1e12)个球

特别地，第j个盒子最多能放i*j个第i种球

求m个盒子能放的最多的球的总数

思路来源

官方题解

题解

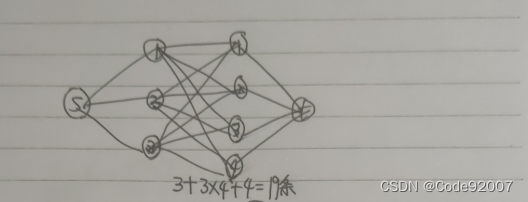
显然是一个最大流模型，超级源点s到超级汇点的流量t，

由于最小割=最大流，可以考虑最后这个图，割完之后长什么样

比如左侧1、3记为集合P含于S，右侧点2记为集合Q含于S，

那么，记左侧集合非P含于T，右侧集合非Q含于T

那么，最小割的边集的构成，由三部分组成：

1. 超级源点s与集合非P之间的边，即左侧属于t的点，断开与s的边

2. 集合Q与超级汇点t之间的边，即右侧属于s的点，断开与t的边

3. 左侧集合P与右侧集合非Q之间的边，左侧属于s的点，右侧属于t的点，断开左右点之间的边

由于边是有向的，

所以无需断开左侧属于t的点和右侧属于s的点之间的边，

因为从上游流量就已经切断了

然后就是对官方题解的一些补充说明吧，

最小割的代价由三部分组成，

形如

所以枚举，也就是左侧属于S集合的i之和，

这样可以通过dp，O(n^3)求得，

也就是属于S集合i之和固定时，不属于S集合的Ai之和的最小值

而后面两坨，k固定时，答案之和j有关，

可以任意划分，将一部分划给S集合，另一部分划给T集合，

并且划给S集合的每个点贡献是j*k，划给T集合的每个点贡献是B[j]，

使得这两部分之和最小，那么考虑某一个点，自然是哪个小划给哪边，

所以每个点贡献是min(j*k,B[j])

由j*k>B[j]，解得k>=B[j]/j，所以枚举k的时候，每个点从S换到T的操作只会发生一次

记录一下这个翻转的时机，即可一边枚举k一边实现对贡献的统计，

这部分复杂度O(n^2+m)

总复杂度O(n^3+n^2+m)

代码

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=505,M=5e5+10,S=N*(N+1)/2;
const ll INF=0x3f3f3f3f3f3f3f3fll;
int n,m;
ll a[N],b[M],dp[N][S],ans,sum,sum2;
vector<int>flip[S];
void upd(ll &x,ll y){
    x=min(x,y);
}
int main(){
    sci(n),sci(m);
    rep(i,1,n)scll(a[i]);
    rep(i,1,m)scll(b[i]);
    memset(dp,INF,sizeof dp);
    dp[0][0]=0;
    rep(i,0,n-1){
        int up=i*(i+1)/2,v=i+1;
        rep(j,0,up){
            upd(dp[i+1][j+v],dp[i][j]);
            upd(dp[i+1][j],dp[i][j]+a[i+1]);
        }
    }
    int lim=n*(n+1)/2;
    rep(j,1,m){//先认为都是j*k，再翻到b[j]
        ll v=b[j]/j;
        if(v<=lim)flip[v].pb(j);
        sum+=j;
    }
    ans=8e18;
    rep(j,0,lim){
        ans=min(ans,dp[n][j]+1ll*sum*j+sum2);
        for(auto &v:flip[j]){
            sum-=v;
            sum2+=b[v];
        }
    }
    printf("%lld\n",ans);
    return 0;
}