泰坦尼克号Titanic生存分析（SPSS、R）_spss 泰坦尼克号

泰坦尼克号Titanic生存分析

记录使用Titanic数据进行分析的过程（新手一个）

• 更新：之前的分析只针对了logistic的模型进行预测，主要使用了 SPSS，近期学习了随机森林和SVM分类器，再使用R进行建模预测，比较模型，查看预测结果。

- 简单介绍Logistic回归

• Logistic回归(Logistic regression，对数线性模型) 与多重线性回归有很多相同之处，最大区别就在于他们之间的因变量不同，它将线性回归结果，通过Logistic函数生成概率，从而进行分类。
• 尽管Logistic函数是非线性的（S形，平滑），然而它的功能只是生成概率，而不是非线性划分数据。
• Logistic回归主要是解决因变量为离散的情况，也就是分类变量，二分问题及其以上（如本题中的存活情况为因变量，存活为1，死亡为0的情况）。

-简单介绍SVM（支持向量机）

• SVM是解决二分类问题的一个分类器，通过寻找一个超平面（如下图所示）将两个类别的样本分开来。通过计算损失函数：所有误分类的点到超平面的距离之和最小，进行计算分类。（改图来自搜狗百科）
  

• SVM分为线性可分（linearseparability）SVM，线性可分也就如上图所示，直接使用一个超平面可直接将样本点分为两类；线性不可分（nonlinear）SVM，下图为线性不可分情形，将其映射到高维空间进行分类。本文采用了线性不可分的情形对泰坦尼克生存分析进行计算预测。
  

-简单介绍随机森林

• 随机森林是包含多个决策树的分类器。一个测试样本会送到每一棵决策树中进行分类预测，然后进行投票，得票最多的类为最终分类结果。对于回归问题随机森林的预测输出是所有决策树输出的均值。
• 每个测试样本都是利用Bootstrap抽样（有放回的抽样）进行抽取样本，再将样本放在决策树中进行分类预测（从n个训练案例中以可重复取样的方式，取样m次，形成一组训练集）

- 题目及变量解释
利用logistic回归（二元选择模型）对该数据进行简单建模及预测

题目：根据给定 Titanic 数据进行建模并对test数据的存活情况进行预测。

• 关于给出的数据集的变量说明：
  Passengerld： 乘客ID
  Survival： 是否存活 0 = No, 1 = Yes
  Pclass： 船舱等级 1 = upper, 2 = middle, 3 = lower
  Sex ： 性别
  Age： 年龄
  sibsp： 兄弟姐妹、配偶数量
  parch： 父母或子女数量
  ticket： 乘客的船票号
  fare： 票价
  cabin： 船舱
  embarked：登船地点 C = Cherbourg, Q = Queenstown, S =
  Southampton
  考虑到乘客ID对模型建立并无用处，直接进行剔除
  乘客姓名，由于其相关信息复杂，本文先不做分析，将其剔除。

查看数据基本信息

从表中的基本信息可以看到9个变量的基本统计信息
总共有891个数据量
关于年龄的平均值为29岁，有177个缺失值；乘客船舱信息有692个缺失值；乘客登船地点有2个缺失值

查看存活率
存活率为：38.4%

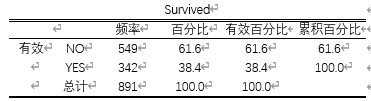
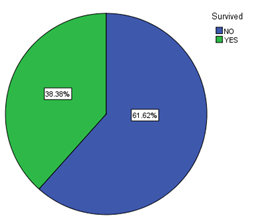
分析查看其它因子下的存活率情况：

不同船舱下的存活率情况，
可以明显看到1级船舱的存活率明显是最高的

查看性别与生存率的关系：
明显看到女性的生存率远远高于男性，女士优先

交叉查看不同船舱下不同性别的存活情况：
从以下信息看到1号船舱的女性多于男性，且获救比例最大。

查看兄弟姐妹配偶数量与生存率的关系：
可以看到该数量在1的情况下的生存率是相较于0的情况下是较高的；其他数量下数量较少


查看父母或子女数量与生存率的关系：
数量为3以后数量较少不做比较
父母或子女数量在1~2之间的存活率大于数量为0的情况；与上述情况一致，考虑到可能与家庭成员的有关系，当生存时可能与其家人一同。

查看乘客上船起始点与生存率的关系：
考虑到可能乘客上船地点的不同与生存率有一定关系，C地点上船的人的存活率高于其他两个地点。

查看年龄对存活率的影响：
得到0-10岁左右的存活率都与死亡率相近或高出一点，40岁以下的存活率都较高，40以上的存活率较低

以下是绘制的年龄面积图：查看年龄的分布情况

缺失值处理

对年龄的缺失值进行填补，SPSS中有以下几种方式：

1. 序列平均值
2. 邻近点平均值
3. 邻近点中位数
4. 线性插值
5. 临近点线性趋势
   这里先采用线性插值的方式对年龄的缺失值进行处理。

处理登船你地点的缺失值：
由与登船地点的缺失值较少，只有2个，对其进行删除处理（删除他所在的两个个案）

相关性分析

给出除编号、姓名、乘客船票号以外变量的与存活情况之间的相关性
观察以下显著性看到Sibsp和Cabin是不显著的，Cabin缺失较多，去掉观察：

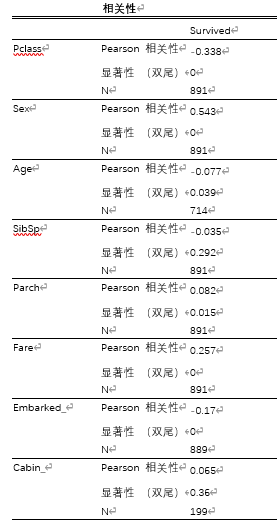
以下为去掉Cabin的相关性：
去掉Cabin后所有变量均显著

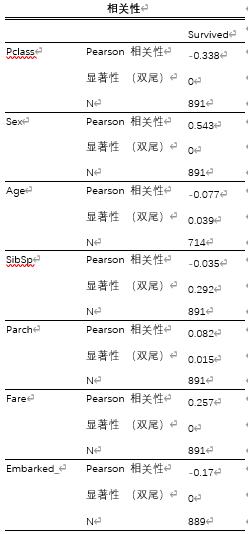
建立Logistic模型

根据上述分析，将
因变量：Survival
自变量：Pclass（1 = upper, 2 = middle, 3 = lower）
Sex（male=0, female=1）、Age、sibsp、parch、fare
Embarked（C=1, Q=2, S=3）
这几个变量分别纳入模型中，进行Logistic回归，初步分析
结果如下：
训练集预测正确率为80%

下面为模型系数及显著性情况：

测试集计算，提交kaggle结果评分为：

模型改进

• 由于前面对于对年龄的缺失值填补不够具有说服性进行相应改进，前面分析中直接舍去了name，观察到name里有Mr、Miss、Mrs等，根据此对年龄分别进行均值填充，提取姓名里的Mr、Miss、Mrs等进行均值填充缺失值。
  对此编写了相应的R代码，如下：

install.packages("stringr")  #字符串处理包
library("stringr")
install.packages("gdata&
1
2