堆排序及复杂度分析_堆复杂度

 

什么是堆？

可以理解为 堆就是一棵完全二叉树。

完全二叉树：假设一棵二叉树的深度是h，若其满足第1~(h-1)层的节点数达到最大个数，第h层的节点都连续出现在最左边，我们称其为完全二叉树。
 

堆又分为 大顶堆和小顶堆。

• 大顶堆：父节点的值大于其左右叶子节点的值。
• 小顶堆：父节点的值小于其左右叶子节点的值。

 

如何构建一个堆？

以数组arr = [3, 8, 5, 2, 9, 5]，我们可以把数组表示成堆的形式，如下图。

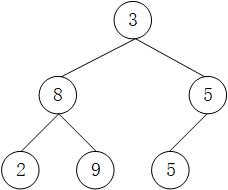
如果已知下标 i，则 其父节点的下标为 (i-1) // 2，左孩子的下标为 2 * i + 1，右孩子的下标为 2 * i + 2。
 
如何把一个堆，转化为大顶堆呢？

基本思路： 遍历数组arr，比较子节点与其父节点，若子节点大于父节点，交换二者的值。

第一步：访问下标0，arr[0] = 3，其为根节点，没有父节点，不做比较。

第二步：访问下标1，arr[1] = 8，比较8与其父节点3，交换3和8，得到 arr = [8, 3, 5, 2, 9, 5]。如下图。

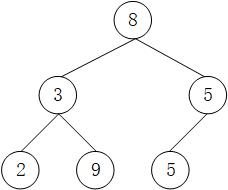
第三步：访问下标2，arr[2] = 5，5小于其父节点8，不做交换。

第四步：访问下标3，arr[3] = 2，2小于其父节点3，不做交换。

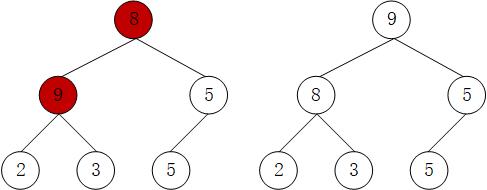
第五步：访问下标4，arr[4] = 9，9大于其父节点3，交换9和3。注意，此时并没有结束，9和3交换后，9大于8，仍需继续交换8和9。得到 arr = [9, 8, 5, 2, 3, 5]，如下图。

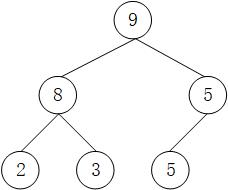
第六步：访问下标5，arr[5] = 5，5等于其父节点5，不做交换。最终得到大顶堆 arr = [9, 8, 5, 2, 3, 5]。

 

代码实现

def build_heap(arr, i):
    # 当子节点大于父节点时 交换
    while (arr[i] > arr[(i - 1) // 2] and i > 0):
        arr[i], arr[(i - 1) // 2] = arr[(i - 1) // 2], arr[
1
2
3