算法设计与分析实验二：动态规划法求解TSP问题和01背包问题_实验2. 基于动态规划法的0-1背包问题求解算法

【实验内容】
（1）tsp问题：利用动态规划算法编程求解TSP问题，并进行时间复杂性分析。
输入：n个城市,权值，任选一个城市出发；
输出：以表格形式输出结果，并给出向量解和最短路径长度。
（2）01背包问题：利用动态规划算法编程求解0-1背包问题，并进行时间复杂性分析。
输入:n个物品，重量为{w1, w2, … ,wn}、价值为{v1, v2, … ,vn}，容量为C的背包；
输出：表格输出结果，并给出向量解和最优值。

【编译环境】devc++ 5.11

【解题思路】
tsp问题：
1.输入图的结点个数和代价矩阵

2.按顺序生成集合的子集

3.动态规划法依次处理子集

4.对于复杂性

【参考内容】
d[i][j]表示从顶点i经过子集v[j]中的顶点一次且仅一次，最后回到出发点0的路径长度。

【代码分析】

一.TSP问题主要解决三个问题

1.顺序表示集合

头文件

#include <stdio.h>
#include<malloc.h>
#include<stdlib.h>
1
2
3

生成集合的函数

long unsigned int* collect(int max)//max表示元素最大值。 
{
	//sum表示子集数量 
	int sum;
	//index指向遍历位置 
	int index = 0; 
	//indexin指向填表位置 
	int indexin = 0;
	//n用来存储中间量 
	unsigned int n=0;
	//组合结果总个数，不包含全空的情况，故减一 
	sum = (int)pow(2,max)-1;
	long unsigned int* col = (long unsigned int*)malloc(sizeof(int)*sum);
	//初始化为二进制1，10，100，1000，10000... 
	//即集合{1，2}表示为011，集合{3}表示为100，通过固定位上是否为1表示集合中是否含有这个数 
	for(int i=0;i<max;i++)
	{
		col[indexin++] = (unsigned int)pow(2,i);
	}
	while(index<=sum)
	{
		for(int i=max-1;i>=0;i--)//从高位判断,集合的最高位方便生成下一位 
		{
			n = (unsigned int)pow(2,i);
			//判断固定位上是否位1 
			if((col[index]&n) != 0 )//！=的优先级大于&运算符的优先级所以要加括号 
			{
				if(i==max-1)
				{
					break;
				}
				for(int j=i+1;j<max;j++)//j<max表示最高生成的集合元素位max 
				{
					//利用加法表示集合001+010相当于集合{1,2} 
					col[indexin++] = col[index]+(unsigned int)pow(2,j);
				}
				break;
			}
		}
		//生成完毕，开始下一次循环 
		index++;
	}
	//方便展示生成的集合 
	/*
	for(int i=0;i<sum;i++)//二进制格式输出 
	{
		char s[max+1];
		itoa(col[i],s,2);
		printf("%s\n",s);
	}
	*/
	return col; 
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

展示生成的集合，形式如下
节点个数为5时：

一些解释

2.从集合中去除一个顶点

因为生成集合的函数使用位数表示集合元素是否存在，所以很方便通过与和非操作去除一个顶点

vindex[j]&(~(long unsigned int)pow(2,h-1))
1

假设vindex[j]为二进制1111即集合{1，2，3，4}
当h为2时，则pow(2,h-1)：10为二进制10即集合{2}
非：1101
再进行与操作：1111与1101->1101即从原集合中去除了元素2。

3.动态规划法依次处理集合和数据

生成数据并初始化第一列数据

头文件和宏定义

#include<time.h> 
#include<random>
#define MAX 999//设置最大权值   
#define MAXNODE 5//节点数 
#define INF 99999//默认最大值 
1
2
3
4
5

数据初始化

int main() { 
	int node;
	 
	//自动生成方式
	//数据写入文件 
	FILE* fp = fopen("demo.TXT","w");
	//生成随机数 
	srand((unsigned)time(NULL));
	node = MAXNODE;
	//生成数组矩阵，用一维数组表示二维数组 
	int *d = (int*)malloc(sizeof(int)*999*999);
	for(int i=0;i<node;i++)
	{
		for(int j=0;j<node;j++)
		{ 
			//行列相等默认最大值 
			if(j == i)
				d[i*node+j] = INF;
			else
				d[i*node+j] = rand()%MAX+1;
			fprintf(fp, "%d\t",d[i*node+j]);
			fprintf(fp, " ");
		}
		fprintf(fp, "\n");
	}
	//关闭文件 
	fclose(fp);
	//调用tsp函数 
    tsp(d,node);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

TSP算法实现

算法实现按照参考图片中第二步

//d表示数组矩阵。n表示节点个数（包括0节点） 
void tsp(int* d,int n)
{
	//数组的索引序号，表示数组处理的顺序 
	long unsigned int*vindex;
	//数组下标代表不同子集，数组存储相应节点对应的最短路径长度 
	int *v = (int*)malloc(sizeof(int)*n*(int)pow(2,n));
	//记录向量解
	int vec[n*(int)pow(2,n)+1]={0}; 
	//初始化
	for(int i=0;i<n;i++)
	{
		v[i*(int)pow(2,n)+0] = d[i*n+0];
		for(int j=1;j<(int)pow(2,n);j++)
		{
			v[i*(int)pow(2,n)+j] = INF;
		}
	}
	//vindex存储的就是遍历子集的顺序,n-1表示子集元素最多为n-1个，0作为出发点 
	vindex = collect(n-1);
	//以下算法每一步都是解释算法书上的伪代码
	int j=0;
	while(j<pow(2,n-1)-1)//依次处理每一个子集数组v[j] 
	{
		if(j==pow(2,n-1)-2)//此时是全集的情况，输出最短路径 
		{
			long unsigned int min=INF;
			int m=0;
			for(int h=1;h<n;h++)//遍历全集中每一个元素
			{
				if(min>d[0*n+h]+v[h*(int)pow(2,n)+(vindex[j]&(~(long unsigned int)pow(2,h-1)))])
				{
					min=d[0*n+h]+v[h*(int)pow(2,n)+(vindex[j]&(~(long unsigned int)pow(2,h-1)))];
					vec[0*((int)pow(2,n)+1)+vindex[j]]=h;
				}				
			}
			v[0*(int)pow(2,n)+vindex[j]]=min;
			
			break;//跳出循环直接输出 
		}
		//开始处理每一个子集
		for(int i=1;i<n;i++)
		{
			if((vindex[j]&(int)pow(2,i-1))==0)//v[j]中不包含i 
			{
				long unsigned int min=INF;
				//对Vindex[j]中每一个元素h，计算v[i][j]=min{d[i][h]+v[h][j-1]}
				for(int h=1;h<n;h++)//遍历每一个元素，计算最小路径 
				{
					if((vindex[j]&(long unsigned int)pow(2,h-1))!=0)//判断元素h在vindex[j]中 
					{
						if(min>d[i*n+h]+v[h*(int)pow(2,n)+(vindex[j]&(~(long unsigned int)pow(2,h-1)))])
						{
							min=d[i*n+h]+v[h*(int)pow(2,n)+(vindex[j]&(~(long unsigned int)pow(2,h-1)))];
							vec[i*((int)pow(2,n)+1)+vindex[j]]=h;
						}
					}
				}
				v[i*(int)pow(2,n)+vindex[j]]=min;
			}
		}
		j++; 
	}
	//打印表格，向量解，最短路径长度 
	printout(d,v,vindex,vec,n);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

输出函数

void printout(int*d,int*v,unsigned long int*vindex,int*vec,int n)
{
		//输出表格
	printf("\t%-8d",0);
	for(int i=0;i<pow(2,n-1)-1;i++)//二进制格式输出 
	{
		char s[n];
		itoa(vindex[i],s,2);
		printf("%-8s",s);
	}
	printf("\n");
	for(int i=0;i<n;i++)
	{
		printf("%-8d",i);
		if(d[i*n+0]<INF)
			printf("%-8d",d[i*n+0]);
		else
			printf("%-8d",0);
		for(int j=0;j<pow(2,n-1)-1;j++)
		{
			if(v[i*(int)pow(2,n)+vindex[j]]>=INF)
				printf("%-8d",0);
			else
				printf("%-8d",v[i*(int)pow(2,n)+vindex[j]]);
		}
		printf("\n");
	}
	//输出向量解
	//记录每一层循环里最小的值作为下一个节点
	int maxcomb=pow(2,n-1)-2;//减去空集减去全集减去编号从0开始造成的偏移，所以减3 
	int last;
	int nextlast = vec[0*((int)pow(2,n)+1)+vindex[(int)pow(2,n-1)-2]];
	int vecindex= vindex[(int)pow(2,n-1)-2];//全集的第一个向量 
	unsigned long int min;
	printf("向量解：<%d->%d> ",0,nextlast);
	for(int j=n;j>1;j--)//寻找n次向量解,每个阶段一次 
	{
		if(j==2)
		{
			printf("<%d->%d> \n",nextlast,0);
			break;
		}
		last = nextlast;
		vecindex = (vecindex&(~(long unsigned int)pow(2,last-1)));//集合中删除last 
		nextlast = vec[last*((int)pow(2,n)+1)+vecindex]; 
		printf("<%d->%d> ",last,nextlast);
	}
	//输出最短路径长度 
	printf("最短路径：%ld",v[vindex[(int)pow(2,n-1)-2]]);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

输出

数据

4.复杂度分析

5.TSP问题源代码

#include <stdio.h>
#include<malloc.h>
#include<time.h> 
#include<random>
#include<stdlib.h>
//宏定义区 
#define MAX 99//设置最大权值   
#define MAXNODE 5//节点数 
#define INF 9999//默认最大值 

//全局变量区

//函数声明区
void tsp(int*,int); 
long unsigned int* collect(int);
void printout(int*,int*,unsigned long int*,int*,int);//数组矩阵,子集值，子集索引，子集向量解，最大元素 


int main() { 
	int node;
	 
	//自动生成方式
	//数据写入文件 
	FILE* fp = fopen("demo.TXT","w");
	//生成随机数 
	srand((unsigned)time(NULL));
	node = MAXNODE;
	//生成数组矩阵，用一维数组表示二维数组 
	int *d = (int*)malloc(sizeof(int)*999*999);
	for(int i=0;i<node;i++)
	{
		for(int j=0;j<node;j++)
		{ 
			//行列相等默认最大值 
			if(j == i)
				d[i*node+j] = INF;
			else
				d[i*node+j] = rand()%MAX+1;
			fprintf(fp, "%d\t",d[i*node+j]);
			fprintf(fp, " ");
		}
		fprintf(fp, "\n");
	}
	//关闭文件 
	fclose(fp);
	//调用tsp函数 
    tsp(d,node);
}


long unsigned int* collect(int max)//max表示元素最大值。 
{
	//sum表示子集数量 
	int sum;
	//index指向遍历位置 
	int index = 0; 
	//indexin指向填表位置 
	int indexin = 0;
	//n用来存储中间量 
	unsigned int n=0;
	//组合结果总个数，不包含全空的情况，故减一 
	sum = (int)pow(2,max)-1;
	long unsigned int* col = (long unsigned int*)malloc(sizeof(int)*sum);
	//初始化为二进制1，10，100，1000，10000... 
	//即集合{1，2}表示为011，集合{3}表示为100，通过固定位上是否为1表示集合中是否含有这个数 
	for(int i=0;i<max;i++)
	{
		col[indexin++] = (unsigned int)pow(2,i);
	}
	while(index<=sum)
	{
		for(int i=max-1;i>=0;i--)//从高位判断,集合的最高位方便生成下一位 
		{
			n = (unsigned int)pow(2,i);
			//判断固定位上是否位1 
			if((col[index]&n) != 0 )//！=的优先级大于&运算符的优先级所以要加括号 
			{
				if(i==max-1)
				{
					break;
				}
				for(int j=i+1;j<max;j++)//j<max表示最高生成的集合元素位max 
				{
					//利用加法表示集合001+010相当于集合{1,2} 
					col[indexin++] = col[index]+(unsigned int)pow(2,j);
				}
				break;
			}
		}
		//生成完毕，开始下一次循环 
		index++;
	}
	//方便展示生成的集合 
	/*
	for(int i=0;i<sum;i++)//二进制格式输出 
	{
		char s[max+1];
		itoa(col[i],s,2);
		printf("%s\n",s);
	}
	*/
	return col; 
}

void printout(int*d,int*v,unsigned long int*vindex,int*vec,int n)
{
		//输出表格
	printf("\t%-8d",0);
	for(int i=0;i<pow(2,n-1)-1;i++)//二进制格式输出 
	{
		char s[n];
		itoa(vindex[i],s,2);
		printf("%-8s",s);
	}
	printf("\n");
	for(int i=0;i<n;i++)
	{
		printf("%-8d",i);
		if(d[i*n+0]<INF)
			printf("%-8d",d[i*n+0]);
		else
			printf("%-8d",0);
		for(int j=0;j<pow(2,n-1)-1;j++)
		{
			if(v[i*(int)pow(2,n)+vindex[j]]>=INF)
				printf("%-8d",0);
			else
				printf("%-8d",v[i*(int)pow(2,n)+vindex[j]]);
		}
		printf("\n");
	}
	//输出向量解
	//记录每一层循环里最小的值作为下一个节点
	int maxcomb=pow(2,n-1)-2;//减去空集减去全集减去编号从0开始造成的偏移，所以减3 
	int last;
	int nextlast = vec[0*((int)pow(2,n)+1)+vindex[(int)pow(2,n-1)-2]];
	int vecindex= vindex[(int)pow(2,n-1)-2];//全集的第一个向量 
	unsigned long int min;
	printf("向量解：<%d->%d> ",0,nextlast);
	for(int j=n;j>1;j--)//寻找n次向量解,每个阶段一次 
	{
		if(j==2)
		{
			printf("<%d->%d> \n",nextlast,0);
			break;
		}
		last = nextlast;
		vecindex = (vecindex&(~(long unsigned int)pow(2,last-1)));//集合中删除last 
		nextlast = vec[last*((int)pow(2,n)+1)+vecindex]; 
		printf("<%d->%d> ",last,nextlast);
	}
	//输出最短路径长度 
	printf("最短路径：%ld",v[vindex[(int)pow(2,n-1)-2]]);
}

//d表示数组矩阵。n表示节点个数（包括0节点） 
void tsp(int* d,int n)
{
	//数组的索引序号，表示数组处理的顺序 
	long unsigned int*vindex;
	//数组下标代表不同子集，数组存储相应节点对应的最短路径长度 
	int *v = (int*)malloc(sizeof(int)*n*(int)pow(2,n));
	//记录向量解
	int vec[n*(int)pow(2,n)+1]={0}; 
	//初始化
	for(int i=0;i<n;i++)
	{
		v[i*(int)pow(2,n)+0] = d[i*n+0];
		for(int j=1;j<(int)pow(2,n);j++)
		{
			v[i*(int)pow(2,n)+j] = INF;
		}
	}
	//vindex存储的就是遍历子集的顺序,n-1表示子集元素最多为n-1个，0作为出发点 
	vindex = collect(n-1);
	//以下算法每一步都是解释算法书上的伪代码，vec数组用于后面方便输出
	int j=0;
	while(j<pow(2,n-1)-1)//依次处理每一个子集数组v[j] 
	{
		if(j==pow(2,n-1)-2)//此时是全集的情况，输出最短路径 
		{
			long unsigned int min=INF;
			int m=0;
			for(int h=1;h<n;h++)//遍历全集中每一个元素
			{
				if(min>d[0*n+h]+v[h*(int)pow(2,n)+(vindex[j]&(~(long unsigned int)pow(2,h-1)))])
				{
					min=d[0*n+h]+v[h*(int)pow(2,n)+(vindex[j]&(~(long unsigned int)pow(2,h-1)))];
					vec[0*((int)pow(2,n)+1)+vindex[j]]=h;
				}				
			}
			v[0*(int)pow(2,n)+vindex[j]]=min;
			
			break;//跳出循环直接输出 
		}
		//开始处理每一个子集
		for(int i=1;i<n;i++)
		{
			if((vindex[j]&(int)pow(2,i-1))==0)//v[j]中不包含i 
			{
				long unsigned int min=INF;
				//对Vindex[j]中每一个元素h，计算v[i][j]=min{d[i][h]+v[h][j-1]}
				for(int h=1;h<n;h++)//遍历每一个元素，计算最小路径 
				{
					if((vindex[j]&(long unsigned int)pow(2,h-1))!=0)//判断元素h在vindex[j]中 
					{
						if(min>d[i*n+h]+v[h*(int)pow(2,n)+(vindex[j]&(~(long unsigned int)pow(2,h-1)))])
						{
							min=d[i*n+h]+v[h*(int)pow(2,n)+(vindex[j]&(~(long unsigned int)pow(2,h-1)))];
							vec[i*((int)pow(2,n)+1)+vindex[j]]=h;
						}
					}
				}
				v[i*(int)pow(2,n)+vindex[j]]=min;
			}
		}
		j++; 
	}
	//打印表格，向量解，最短路径长度 
	printout(d,v,vindex,vec,n);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222

二.01背包问题

【解题思路】
1.获取背包容量packvol，物品数量n，物品价值和重量value[],weigth[]

2.动态规划法求解01背包问题

3.对于复杂性
【参考内容】
背包最大价值

装入背包的物品


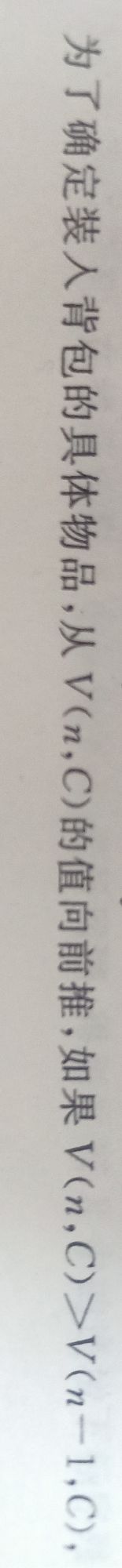
【代码分析】

1.动态规划法求解背包最大价值

初始化

	//价值矩阵 
	int v[n+1][packvol+1]={0};
	//背包是否装入物品 
	int x[n+1]; 
	//初始化第0行和第0列 
	for(int i=0;i<=packvol;i++)
	{
		v[0][i]=0;
	}
	for(int i=0;i<=n;i++)
	{
		v[i][0]=0;
		x[i]=0;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

动态规划法遍历价值矩阵

	//依次遍历数组 
	for(int i=1;i<=n;i++)//物品 
	{
		for(int j=1;j<=packvol;j++)//背包容量 
		{
			if(weight[i-1]>j)//装不下 
				v[i][j]=v[i-1][j];
			if(weight[i-1]<=j)//装的下，继续判断是否最优 
			{
				v[i][j] = v[i-1][j-weight[i-1]]+value[i-1]>v[i-1][j]?v[i-1][j-weight[i-1]]+value[i-1]:v[i-1][j];
			}
		}
	}
1
2
3
4
5
6
7
8
9
10
11
12
13

2.按要求输出

表格

	//输出表格
	for(int i=0;i<=n;i++)
	{
		for(int j=0;j<=packvol;j++)
		{
			printf("%-4d",v[i][j]);//左对齐输出 
		}
		printf("\n");
	}
1
2
3
4
5
6
7
8
9

向量解

	//向量解
	printf("向量解{行，列}：");
	for(int i=n,j=packvol;i>0;i--)
	{
		printf("{%d,%d}->",i,j);
		if(v[i][j]>v[i-1][j])
		{
			x[i]=1;//参考内容第三个图片 
			j= j-weight[i-1];
		}
		if(i==1)
		{
			printf("{%d,%d}",i-1,j);
		}
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

最优解和最大价值

	//最优解 
	printf("\n最优解："); 
	for(int i=1;i<=n;i++)
	{
		printf("%d",x[i]);
	}
	printf("\n最大价值：%d",v[n][packvol]);
1
2
3
4
5
6
7

输出

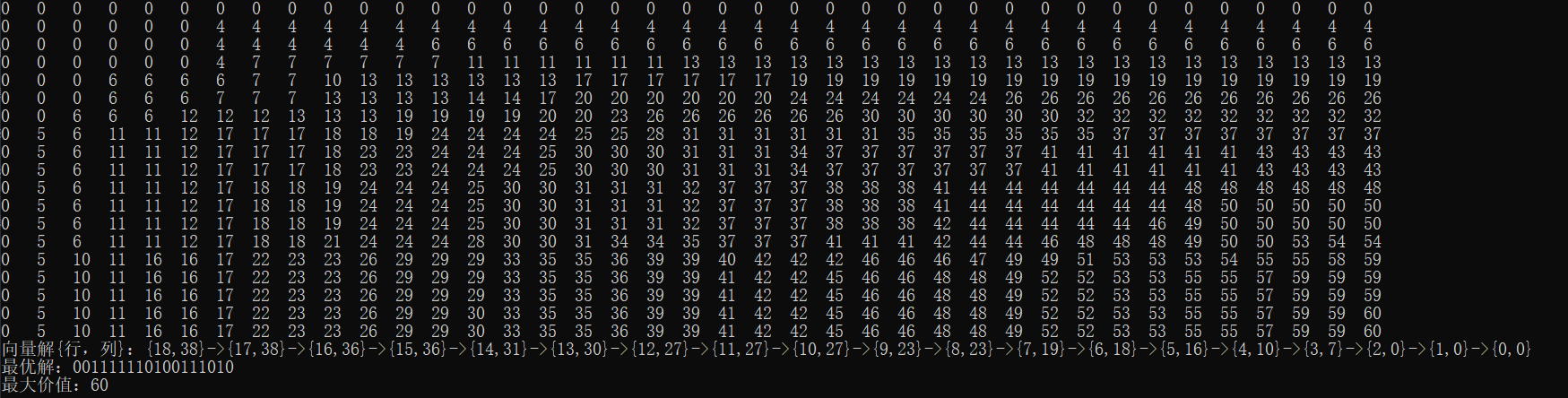
数据

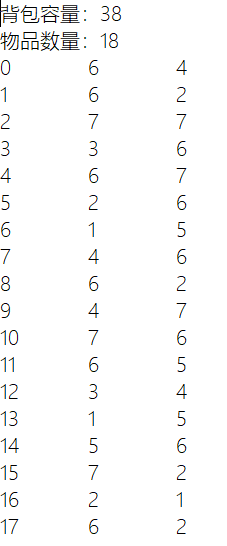
3.复杂度分析

4.01背包问题源代码

#include<stdio.h>
#include<time.h>
#include<random>

//宏定义区 
#define MAX 60//背包最大容量 
#define MAXN 30//最大物品数 
#define MAXW 7//物品最大重量 
#define MAXV 7//物品最大价值 
//全局变量区 


//自定义函数区 
void randomint(int,int,int*,int*);
void fwritein(int,int,int*,int*);
void Pack(int,int,int*,int*);

int main()
{
	int n,packvol;
	srand(time(NULL));
	n = rand()%MAXN;
	packvol = rand()%MAX+1;
	int w[n],v[n];
	randomint(packvol,n,w,v);
	Pack(n,packvol,w,v);
	return 0;
}
 
void fwritein(int packvol,int n,int* weight,int* value)
{
	FILE* fp = fopen("demo2-2.TXT","w");
	fprintf(fp,"背包容量：%d\n",packvol);
	fprintf(fp,"物品数量：%d\n",n);
	for(int i=0;i<n;i++)
	{
		fprintf(fp,"%d\t%d\t%d\n",i,weight[i],value[i]);
	}
	fclose(fp);
}

void randomint(int packvol,int n,int* weight,int* value)
{
	for(int i=0;i<n;i++)
	{
		weight[i]=rand()%MAXW+1;
		value[i]=rand()%MAXV+1;
	}
	fwritein(packvol,n,weight,value);
	return;
}

void Pack(int n,int packvol,int* weight,int* value)
{
	int v[n+1][packvol+1]={0};
	int x[n+1]; 
	for(int i=0;i<=packvol;i++)
	{
		v[0][i]=0;
	}
	for(int i=0;i<=n;i++)
	{
		v[i][0]=0;
		x[i]=0;
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=packvol;j++)
		{
			if(weight[i-1]>j)
				v[i][j]=v[i-1][j];
			if(weight[i-1]<=j)
			{
				v[i][j] = v[i-1][j-weight[i-1]]+value[i-1]>v[i-1][j]?v[i-1][j-weight[i-1]]+value[i-1]:v[i-1][j];
			}
		}
	}
	for(int i=0;i<=n;i++)
	{
		for(int j=0;j<=packvol;j++)
		{
			printf("%-4d",v[i][j]);
		}
		printf("\n");
	}
	printf("向量解{行，列}：");
	for(int i=n,j=packvol;i>0;i--)
	{
		printf("{%d,%d}->",i,j);
		if(v[i][j]>v[i-1][j])
		{
			x[i]=1;
			j= j-weight[i-1];
		}
		if(i==1)
		{
			printf("{%d,%d}",i-1,j);
		}
	}
	printf("\n最优解："); 
	for(int i=1;i<=n;i++)
	{
		printf("%d",x[i]);
	}
	printf("\n最大价值：%d",v[n][packvol]);
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108