二叉树的链式存储及实现（二叉树的前序遍历，中序遍历，后序遍历，非递归前序遍历，中序遍历，后序遍历，二叉树的查找，寻找叶子结点个数，以及判断一棵树是不是二叉树）_二叉树的链式储存二叉树的遍历算法以及利用其解决问题

二叉树的链式存储及实现

1、树的概念及结构

1.1、树的结构

树是一种非线性结构，它由n（n>=0）个有限结点组成的一个具有层次关系的集合。把它叫做树是因为它看起来像一颗倒挂的树，也就是说它是一颗根朝上，叶朝下的。
树的特点：
每个结点有零个或多个子结点；
没有父结点的结点称为根结点；
每一个非根结点有且只有一个父结点；
每个子结点可以分为多个不相交的子树。

1.2、树的表示

树的表示方法：
双亲表示法；
孩子表示法；
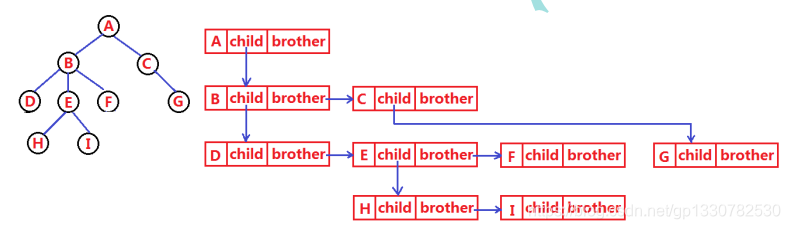
孩子兄弟表示法；

typedef int DataType
struct Node
{
	struct Node *_firstChild1;	//第一个孩子结点
	struct Node *_pNextBrother;//指向下一个兄弟结点
	DataType _data;				//结点中的数据域
}
1
2
3
4
5
6
7

2、二叉树的概念及结构

2.1、二叉树的概念

一颗二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根结点加上两颗别称为左子树和右子树的二叉树组成
二叉树的特点：
每个结点最多有两颗子树，即二叉树不存在度大于2的结点
二叉树的子树有左右之分，其子树的次序不能颠倒

2.2、二叉树的存储结构

2.2.1、顺序存储

顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实使用中只有堆才使用数组来存储，二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。

2.2.2、链式存储

用链表来表示一颗二叉树，即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和在右孩子所在的链结点的存储地址。链式结构又分为二叉链和三叉链。

// 二叉链
struct BinaryTreeNode
{
struct BinTreeNode* _pLeft; // 指向当前节点左孩子
struct BinTreeNode* _pRight; // 指向当前节点右孩子
BTDataType _data; // 当前节点值域
}
1
2
3
4
5
6
7

// 三叉链
struct BinaryTreeNode
{
struct BinTreeNode* _pParent; // 指向当前节点的双亲
struct BinTreeNode* _pLeft; // 指向当前节点左孩子
struct BinTreeNode* _pRight; // 指向当前节点右孩子
BTDataType _data; // 当前节点值域
}；
1
2
3
4
5
6
7
8

3、二叉树遍历

二叉树的遍历指的是访问二叉树的每个结点，并且对每个结点仅做一次访问。访问结点所做的操作依赖于具体的应用问题。遍历二叉树上最重要的运算之一，是二叉树上进行其它运算的基础。

前序遍历
先访问根结点，再访问左孩子，再访问右孩子
中序遍历
先访问左孩子，再访问根结点，最后访问右孩子
后序遍历
先访问左孩子，再访问右孩子，最后访问根结点
层序遍历
逐层访问每个结点

4、二叉树的链式存储及实现

4.1、二叉树的链式结构

typedef char BinaryTreeDataType;

typedef struct BinaryTreeNode
{
	BinaryTreeDataType _data;
	struct BinaryTreeNode *_left;
	struct BinaryTreeNode *_right;
}BinaryTreeNode;
1
2
3
4
5
6
7
8

4.2、二叉树的实现

BinaryTree.h

#ifndef _BINARYTREE_H_
#define _BINARYTREE_H_

#define _CRT_SECURE_NO_WARNINGS

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
#include <math.h>
#include "Queue.h"
#include "Stack.h"

typedef char BinaryTreeDataType;

typedef struct BinaryTreeNode
{
	BinaryTreeDataType _data;
	struct BinaryTreeNode *_left;
	struct BinaryTreeNode *_right;
}BinaryTreeNode;

//通过前序遍历数组"ABD##E#H##CF##G##"构建二叉树
BinaryTreeNode* BinaryTreeCreate(BinaryTreeDataType *arr);

//递归遍历
//前序遍历
void BinaryTreePreOrder(BinaryTreeNode *root);
//中序遍历
void BinaryTreeInOrder(BinaryTreeNode *root);
//后序遍历
void BinaryTreePostOrder(BinaryTreeNode *root);
//层序遍历
void BinaryTreeLevelOrder(BinaryTreeNode *root);

//非递归遍历
//前序遍历
void BinaryTreePreOrderNonR(BinaryTreeNode *root);
//中序遍历
void BinaryTreeInOrderNonR(BinaryTreeNode *root);
//后序遍历
void BinaryTreePostOrderNonR(BinaryTreeNode *root);
//返回二叉树的结点个数
int BinaryTreeSize(BinaryTreeNode *root);

//递归实现
//返回叶子结点个数
int BinaryTreeLeafSize(BinaryTreeNode *root);
//返回第K层结点个数
int BinaryTreeLevelKSize(BinaryTreeNode *root, int k);

//非递归实现
//返回叶子结点个数
int BinaryTreeLeafSizeNonR(BinaryTreeNode *root);
//返回第K层结点个数
int BinaryTreeLevelKSizeNonR(BinaryTreeNode *root, int k);

//查找节点x
BinaryTreeNode* BinaryTreeFind(BinaryTreeNode *root, BinaryTreeDataType x);
//判断是否为完全二叉树
int BinaryTreeComplete(BinaryTreeNode *root);
//销毁
void BinaryTreeDestory(BinaryTreeNode *root);

#endif //_BINARYTREE_H_
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

Queue.h

#ifndef _QUEUE_H_
#define _QUEUE_H_

#define _CRT_SECURE_NO_WARNINGS

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>

typedef int QueueDataType;

typedef struct QueueNode
{
	struct QueueNode *_next;
	QueueDataType _data;
}QueueNode;

typedef struct Queue
{
	QueueNode *_front;
	QueueNode *_rear;
}Queue;

//初始化
void QueueInit(Queue *pqueue);
//销毁
void QueueDestory(Queue *pqueue);
//为链表开辟结点
QueueNode* BuyQueueNode(QueueDataType x);
//尾插
void QueuePush(Queue *pqueue, QueueDataType x);
//头删
void QueuePop(Queue *pqueue);
//返回队首元素
QueueDataType QueueFront(Queue *pqueue);
//返回队尾元素
QueueDataType QueueRear(Queue *pqueue);
//判空
int QueueEmpty(Queue *pqueue);
//返回队列长度
int QueueSize(Queue *pqueue);
//打印
void QueuePrint(Queue *pqueue);
#endif //_QUEUE_H_
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

Stack.h

#ifndef _STACK_H_
#define _STACK_H_

#define _CRT_SECURE_NO_WARNINGS

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>

#define CAPACITY 2

typedef int StackDataType;

typedef struct Stack
{
	StackDataType *_array;
	size_t _size;
	size_t _capacity;
}Stack;

//初始化
void StackInit(Stack *pstack, size_t capacity);
//销毁
void StackDestory(Stack *pstack);
//扩容
void CheckCapacity(Stack *pstack);
//压栈
void StackPush(Stack *pstack, StackDataType x);
//弹出
void StackPop(Stack *pstack);
//返回栈顶元素
StackDataType StackTop(Stack *pstack);
//返回栈的大小
int StackSize(Stack *pstack);
//判空
int StackEmpty(Stack *pstack);
//打印
void StackPrint(Stack *pstack);
#endif //_STACK_H_
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

BinaryTree.c

#include "BinaryTree.h"
#include "Queue.h"
#include "Stack.h"

//通过前序遍历数组"ABD##E#H##CF##G##"构建二叉树
BinaryTreeNode* BinaryTreeCreate(BinaryTreeDataType *arr)
{
	static int i = 0;
	if (arr[i] == '#')
	{
		i++;
		return NULL;
	}
	BinaryTreeNode *cur = (BinaryTreeNode *)malloc(sizeof(BinaryTreeNode));
	cur->_data = arr[i];
	i++;
	cur->_left = BinaryTreeCreate(arr);
	cur->_right = BinaryTreeCreate(arr);
	return cur;
}

//递归遍历
//前序遍历
void BinaryTreePreOrder(BinaryTreeNode *root)
{
	if (root)
	{
		putchar(root->_data);
		BinaryTreePreOrder(root->_left);
		BinaryTreePreOrder(root->_right);
	}
}

//中序遍历
void BinaryTreeInOrder(BinaryTreeNode *root)
{
	if (root)
	{
		BinaryTreeInOrder(root->_left);
		putchar(root->_data);
		BinaryTreeInOrder(root->_right);
	}
}

//后序遍历
void BinaryTreePostOrder(BinaryTreeNode *root)
{
	if (root)
	{
		BinaryTreePostOrder(root->_left);
		BinaryTreePostOrder(root->_right);
		putchar(root->_data);
	}
}

//层序遍历
void BinaryTreeLevelOrder(BinaryTreeNode *root)
{
	BinaryTreeNode *cur;
	Queue queue;
	QueueInit(&queue);
	QueuePush(&queue, root);
	while (!QueueEmpty(&queue))
	{
		cur = QueueFront(&queue);
		putchar(cur->_data);
		if (cur->_left)
		{
			QueuePush(&queue, cur->_left);
		}
		if (cur->_right)
		{
			QueuePush(&queue, cur->_right);
		}
		QueuePop(&queue);
	}
	QueueDestory(&queue);
}

//非递归遍历
//前序遍历
void BinaryTreePreOrderNonR(BinaryTreeNode *root)
{
	BinaryTreeNode *cur = root;
	Stack stack;
	StackInit(&stack, 100);
	while (cur || !StackEmpty(&stack))
	{
		while (cur)
		{
			putchar(cur->_data);
			StackPush(&stack, cur);
			cur = cur->_left;
		}
		if (!StackEmpty(&stack))
		{
			cur = StackTop(&stack);
			StackPop(&stack);
			cur = cur->_right;
		}
	}
	StackDestory(&stack);
}

//中序遍历
void BinaryTreeInOrderNonR(BinaryTreeNode *root)
{
	assert(root);
	BinaryTreeNode *cur = root;
	Stack stack;
	StackInit(&stack, 100);
	while (!StackEmpty(&stack) || cur)
	{
		for (; cur; cur = cur->_left)
		{
			StackPush(&stack, cur);
		}
		cur = StackTop(&stack);
		putchar(cur->_data);
		StackPop(&stack);
		cur = cur->_right;
	}
	StackDestory(&stack);
}

//后序遍历
void BinaryTreePostOrderNonR(BinaryTreeNode *root)
{
	assert(root);
	BinaryTreeNode *cur = root;
	Stack stack;
	char tag[100];
	StackInit(&stack, 100);
	do
	{
		for (; cur; cur = cur->_left)
		{
			StackPush(&stack, cur);
			tag[StackSize(&stack) - 1] = 0;
		}
		while (!StackEmpty(&stack) && tag[StackSize(&stack) - 1])
		{
			cur = StackTop(&stack);
			putchar(cur->_data);
			StackPop(&stack);
		}
		if (!StackEmpty(&stack))
		{
			cur = StackTop(&stack);
			tag[StackSize(&stack) - 1] = 1;
			cur = cur->_right;
		}
	} while (!StackEmpty(&stack));
	StackDestory(&stack);
}

//返回二叉树的结点个数
int BinaryTreeSize(BinaryTreeNode *root)
{
	int count = 0;
	BinaryTreeNode *cur = root;
	Stack stack;
	StackInit(&stack, 100);
	while (cur || !StackEmpty(&stack))
	{
		while (cur)
		{
			//putchar(cur->_data);
			count++;
			StackPush(&stack, cur);
			cur = cur->_left;
		}
		if (!StackEmpty(&stack))
		{
			cur = StackTop(&stack);
			StackPop(&stack);
			cur = cur->_right;
		}
	}
	StackDestory(&stack);
	return count;
}

//递归实现
//返回叶子结点个数
int BinaryTreeLeafSize(BinaryTreeNode *root)
{
	if (root == NULL)
	{
		return 0;
	}
	else if ((root->_left == NULL) && (root->_right == NULL))
	{
		return 1;
	}
	else
	{
		return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
	}
}

//返回第K层结点个数
int BinaryTreeLevelKSize(BinaryTreeNode *root, int k)
{
	if (root == NULL || k <= 0)
	{
		return 0;
	}
	else if (root && k == 1)
	{
		return 1;
	}
	else
	{
		return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
	}
}

//非递归实现
//返回叶子结点个数
int BinaryTreeLeafSizeNonR(BinaryTreeNode *root)
{
	int count = 0;
	BinaryTreeNode *cur = root;
	Stack stack;
	StackInit(&stack, 100);
	while (cur)
	{
		//putchar(cur->_data);
		if (cur->_left == NULL && cur->_right == NULL)
		{
			count++;
		}
		if (cur->_right)
		{
			StackPush(&stack, cur->_right);
		}
		if (cur->_left)
		{
			cur = cur->_left;
		}
		else
		{
			cur = StackTop(&stack);
			StackPop(&stack);
		}
	}
	StackDestory(&stack);
	return count;
}

//返回第K层结点个数
int BinaryTreeLevelKSizeNonR(BinaryTreeNode *root, int k)
{
	if (root == NULL || k <= 0)
	{
		return 0;
	}
	int level = 0;
	int levelsize = 0;
	Queue queue;
	QueueInit(&queue);
	QueuePush(&queue, root);
	while (!QueueEmpty(&queue))
	{
		level++;
		levelsize = QueueSize(&queue);
		if (level == k)
		{
			break;
		}
		int count = 0;
		while (count < levelsize)
		{
			count++;
			BinaryTreeNode *cur = QueueFront(&queue);
			QueuePop(&queue);
			if (cur->_left)
			{
				QueuePush(&queue, cur->_left);
			}
			if (cur->_right)
			{
				QueuePush(&queue, cur->_right);
			}
		}
	}
	QueueDestory(&queue);
	if (level == k)
	{
		return levelsize;
	}
}

//查找节点x
BinaryTreeNode* BinaryTreeFind(BinaryTreeNode *root, BinaryTreeDataType x)
{
	BinaryTreeNode *cur;
	Queue queue;
	QueueInit(&queue);
	QueuePush(&queue, root);
	while (!QueueEmpty(&queue))
	{
		cur = QueueFront(&queue);
		//putchar(cur->_data);
		if (cur->_data == x)
		{
			return cur;
		}
		if (cur->_left)
		{
			QueuePush(&queue, cur->_left);
		}
		if (cur->_right)
		{
			QueuePush(&queue, cur->_right);
		}
		QueuePop(&queue);
	}
	QueueDestory(&queue);
}

//判断是否为完全二叉树
int BinaryTreeComplete(BinaryTreeNode *root)
{
	if (root == NULL)
	{
		return 1;
	}
	BinaryTreeNode *cur;
	Queue queue;
	QueueInit(&queue);
	QueuePush(&queue, root);
	int leaf = 0;
	while (!QueueEmpty(&queue))
	{
		cur = QueueFront(&queue);
		QueuePop(&queue);
		if ((leaf && (cur->_left != NULL || cur->_right != NULL)) || (cur->_left == NULL && cur->_right))
		{
			return 0;
		}
		if (cur->_left != NULL)
		{
			QueuePush(&queue, cur->_left);
		}
		if (cur->_right != NULL)
		{
			QueuePush(&queue, cur->_right);
		}
		if (cur->_left == NULL || cur->_right == NULL)
		{
			leaf = 1;
		}
	}
	return 1;
	QueueDestory(&queue);
}

//销毁
void BinaryTreeDestory(BinaryTreeNode *root)
{
	assert(root);
	if (root)
	{
		BinaryTreePostOrder(root->_left);
		BinaryTreePostOrder(root->_right);
		free(root);
		root = NULL;
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372

Queue.c

#include "Queue.h"

//初始化
void QueueInit(Queue *pqueue)
{
	assert(pqueue);
	pqueue->_front = NULL;
	pqueue->_rear = NULL;
}

//销毁
void QueueDestory(Queue *pqueue)
{
	assert(pqueue);
	QueueNode *cur = pqueue->_front;
	while (cur)
	{
		QueueNode *tmp = cur->_next;
		free(cur);
		cur = tmp;
	}
	pqueue->_front = NULL;
	pqueue->_rear = NULL;
}

//为链表开辟结点
QueueNode* BuyQueueNode(QueueDataType x)
{
	QueueNode *queuenode = (QueueNode *)malloc(sizeof(QueueNode));
	if (queuenode != NULL)
	{
		queuenode->_data = x;
		queuenode->_next = NULL;
		return queuenode;
	}
	return NULL;
}

//尾插
void QueuePush(Queue *pqueue, QueueDataType x)
{
	assert(pqueue);
	QueueNode *queuenode = BuyQueueNode(x);
	if (QueueEmpty(pqueue))
	{
		pqueue->_front = queuenode;
		pqueue->_rear = queuenode;
	}
	else
	{
		pqueue->_rear->_next = queuenode;
		pqueue->_rear = queuenode;
	}
}

//头删
void QueuePop(Queue *pqueue)
{
	assert(pqueue);
	QueueNode *tmp = pqueue->_front;
	pqueue->_front = tmp->_next;
	free(tmp);
	tmp = NULL;
}

//返回队首元素
QueueDataType QueueFront(Queue *pqueue)
{
	assert(pqueue);
	return pqueue->_front->_data;
}

//返回队尾元素
QueueDataType QueueRear(Queue *pqueue)
{
	assert(pqueue);
	return pqueue->_rear->_data;
}

//判空
int QueueEmpty(Queue *pqueue)
{
	assert(pqueue);
	return pqueue->_front == NULL;
}

//返回队列长度
int QueueSize(Queue *pqueue)
{
	assert(pqueue);
	int count = 0;
	QueueNode *cur = pqueue->_front;
	for (; cur; cur = cur->_next)
	{
		count++;
	}
	return count;
}

//打印
void QueuePrint(Queue *pqueue)
{
	assert(pqueue);
	printf("front <== ");
	QueueNode *cur = pqueue->_front;
	for (; cur; cur = cur->_next)
	{
		printf(" %d <==", cur->_data);
	}
	printf(" real\n");
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111

Stack.c

#include "Stack.h"

//初始化
void StackInit(Stack *pstack, size_t capacity)
{
	assert(pstack);
	pstack->_capacity = capacity;
	pstack->_array = (StackDataType *)malloc(capacity*sizeof(StackDataType));
	assert(pstack->_array);
	pstack->_size = 0;
}

//销毁
void StackDestory(Stack *pstack)
{
	assert(pstack);
	if (pstack->_array)
	{
		free(pstack->_array);
		pstack->_array = NULL;
		pstack->_size = 0;
		pstack->_capacity = 0;
	}
}

//扩容
void CheckCapacity(Stack *pstack)
{
	assert(pstack);
	if (pstack->_size == pstack->_capacity)
	{
		pstack->_capacity *= CAPACITY;
		pstack->_array = (StackDataType *)realloc(pstack->_array, pstack->_capacity*sizeof(StackDataType));
	}
}

//压栈
void StackPush(Stack *pstack, StackDataType x)
{
	assert(pstack);
	CheckCapacity(pstack);
	pstack->_array[pstack->_size] = x;
	pstack->_size++;
}

//弹出
void StackPop(Stack *pstack)
{
	assert(pstack || pstack->_size);
	pstack->_size--;
}

//返回栈顶元素
StackDataType StackTop(Stack *pstack)
{
	assert(pstack);
	if (pstack->_array)
	{
		return pstack->_array[pstack->_size - 1];
	}
	return (StackDataType)0;
}

//返回栈的大小
int StackSize(Stack *pstack)
{
	assert(pstack);
	assert(pstack);
	if (pstack->_array)
	{
		return pstack->_size;
	}
	return -1;
}

//判空
int StackEmpty(Stack *pstack)
{
	assert(pstack);
	return pstack->_size == 0;
}

//打印
void StackPrint(Stack *pstack)
{
	assert(pstack);
	for (int i = 0; i < pstack->_size; i++)
	{
		printf("%d--", pstack->_array[i]);
	}
	printf("Top\n");
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92

main.c

#include "BinaryTree.h"
#include "Queue.h"
#include "Stack.h"

int main()
{
	BinaryTreeDataType arr[] = "ABD##E#H##CF##G##";
	BinaryTreeNode *root = BinaryTreeCreate(arr);

	BinaryTreePreOrder(root);
	putchar('\n');
	BinaryTreeInOrder(root);
	putchar('\n');
	BinaryTreePostOrder(root);
	putchar('\n');
	BinaryTreeLevelOrder(root);
	putchar('\n');
	BinaryTreePreOrderNonR(root);
	putchar('\n');
	BinaryTreeInOrderNonR(root);
	putchar('\n');
	BinaryTreePostOrderNonR(root);
	putchar('\n');
	printf("BinaryTreeSize = %d\n", BinaryTreeSize(root));
	printf("BinaryTreeLeafSize = %d\n", BinaryTreeLeafSize(root));
	printf("BinaryTreeLevelKSize = %d\n", BinaryTreeLevelKSize(root, 1));
	printf("BinaryTreeLevelKSize = %d\n", BinaryTreeLevelKSize(root, 2));
	printf("BinaryTreeLevelKSize = %d\n", BinaryTreeLevelKSize(root, 3));
	printf("BinaryTreeLevelKSize = %d\n", BinaryTreeLevelKSize(root, 4));
	printf("BinaryTreeFind = %p\n", BinaryTreeFind(root, 'G'));
	printf("BinaryTreeComplete = %d\n", BinaryTreeComplete(root));
	printf("BinaryTreeLevelKSizeNonR = %d\n", BinaryTreeLevelKSizeNonR(root, 1));
	printf("BinaryTreeLevelKSizeNonR = %d\n", BinaryTreeLevelKSizeNonR(root, 2));
	printf("BinaryTreeLevelKSizeNonR = %d\n", BinaryTreeLevelKSizeNonR(root, 3));
	printf("BinaryTreeLevelKSizeNonR = %d\n", BinaryTreeLevelKSizeNonR(root, 4));

	system("pause");
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40