用Python标准GUI库Tkinter绘制分形图_python分形绘图

用Python标准GUI库Tkinter绘制分形图

分形图是一种通过迭代规则生成自相似图案的艺术形式。

分形图包括曼德勃罗集、科赫曲线、谢尔宾斯基三角等代码等。

Tkinter是Python的标准GUI库，可以用于创建窗口、控件和其他图形界面元素。绘制分形图像，如曼德勃罗集或科赫曲线，通常需要利用递归和迭代的数学原理。需要注意的是，绘制分形图可能需要一些时间，尤其是当分形的迭代等级变高时。

下面使用Python的标准GUI库Tkinter实现曼德勃罗集、科赫曲线、谢尔宾斯基三角。

一、曼德勃罗集

先给出效果图

源码如下：

import tkinter as tk
 
# 设置画布大小和坐标范围
width, height = 400, 400
x_min, x_max = -2.0, 1.0
y_min, y_max = -1.5, 1.5
 
# 定义颜色映射函数
def color_map(n, max_iter):
    r, g, b = 0, 0, 0
    if n < max_iter:
        r = int((n / max_iter) * 255)
        g = int((n / max_iter) * 255)
        b = int((n / max_iter) * 255)
    return "#{:02x}{:02x}{:02x}".format(r, g, b)
 
# 绘制曼德勃罗集
def mandelbrot(canvas):
    max_iter = 100  # 最大迭代次数
 
    for x in range(width):
        for y in range(height):
            zx, zy = 0, 0
            cx = x_min + (x / width) * (x_max - x_min)
            cy = y_min + (y / height) * (y_max - y_min)
            c = complex(cx, cy)
 
            for i in range(max_iter):
                if abs(zx + zy) > 2.0:
                    break
                zx, zy = zx * zx - zy * zy + cx, 2.0 * zx * zy + cy
 
            # 绘制像素点并填充颜色
            color = color_map(i, max_iter)
            canvas.create_rectangle(x, y, x + 1, y + 1, fill=color, outline="")
 
# 创建窗口和画布
window = tk.Tk()
canvas = tk.Canvas(window, width=width, height=height)
canvas.pack()
 
# 调用绘制函数
mandelbrot(canvas)
 
# 运行窗口主循环
window.mainloop()

提示：这个分形图从运行到出图有点慢——需要一些时间。

二、科赫曲线

先给出效果图

源码如下：

# 科赫曲线
import tkinter as tk
from math import sqrt
 
def koch_line(canvas, p1, p2, level):
    if level == 0:
        canvas.create_line(p1, p2)
    else:
        dx = (p2[0] - p1[0]) / 3
        dy = (p2[1] - p1[1]) / 3
        
        p3 = (p1[0] + dx, p1[1] + dy)
        p5 = (p1[0] + 2*dx, p1[1] + 2*dy)
        x = p3[0] + (dx - dy * sqrt(3)) / 2
        y = p3[1] + (dx * sqrt(3) + dy) / 2
        p4 = (x, y)
        
        koch_line(canvas, p1, p3, level - 1)
        koch_line(canvas, p3, p4, level - 1)
        koch_line(canvas, p4, p5, level - 1)
        koch_line(canvas, p5, p2, level - 1)
 
def draw_koch_snowflake():
    root = tk.Tk()
    root.title("Koch Snowflake")
    canvas = tk.Canvas(root, width=650, height=650, bg="white")
    canvas.pack()
    
    p1 = (100, 500)
    p2 = (500, 500)
    p3 = (300, 500 - (400 * sqrt(3) / 2))
    
    koch_line(canvas, p1, p2, 4)
    koch_line(canvas, p2, p3, 4)
    koch_line(canvas, p3, p1, 4)
    
    root.mainloop()
 
draw_koch_snowflake()

三、谢尔宾斯基三角

先给出效果图

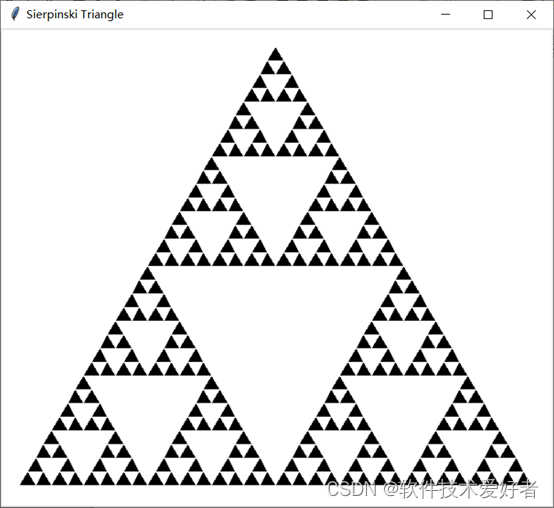
源码如下：

# 谢尔宾斯基三角
import tkinter as tk
 
def sierpinski_triangle(canvas, vertices, level):
    x1, y1 = vertices[0]
    x2, y2 = vertices[1]
    x3, y3 = vertices[2]
    
    if level == 0:
        canvas.create_polygon(x1, y1, x2, y2, x3, y3, fill="black")
    else:
        x12 = (x1 + x2) / 2
        y12 = (y1 + y2) / 2
        x23 = (x2 + x3) / 2
        y23 = (y2 + y3) / 2
        x31 = (x3 + x1) / 2
        y31 = (y3 + y1) / 2
        
        sierpinski_triangle(canvas, [(x1, y1), (x12, y12), (x31, y31)], level - 1)
        sierpinski_triangle(canvas, [(x12, y12), (x2, y2), (x23, y23)], level - 1)
        sierpinski_triangle(canvas, [(x31, y31), (x23, y23), (x3, y3)], level - 1)
 
root = tk.Tk()
root.title("Sierpinski Triangle")
canvas = tk.Canvas(root, width=600, height=520, bg="white")
canvas.pack()
sierpinski_triangle(canvas, [(300, 20), (20, 500), (580, 500)], 5)
root.mainloop()
 

附录

Python 分形算法__代码里开出来的艺术之花https://zhuanlan.zhihu.com/p/489274872