CF Round 944 （div.4）ABCDEFG

A题：

解答：

无脑min()和max()

#include<bits/stdc++.h>
using namespace std;
 
void solve(){
    int a,b;
    cin>>a>>b;
    cout<<min(a,b)<<" "<<max(a,b)<<endl;
}
 
int main(){
    int _;
    cin>>_;
    while(_--){
        solve();
    }
    return 0;
}

B题：

解答：

如果字符串s只包含一种字符，，则无法重新排列出一个与原串不相同的新的字符串。

如果可以排列，一种可能的排列思路是：交换第一个相邻不同字符在s中的位置得到r

#include<bits/stdc++.h>
using namespace std;
 
void solve(){
    string a;
    set<char>s;
    cin>>a;
    for(int i=0;a[i];i++){
        s.insert(a[i]);
    }
    if(s.size()==1)cout<<"NO"<<endl;
    else {
        cout<<"YES"<<endl;
        for(int i=1;i<a.size();i++){
            if(a[i-1]!=a[i]){
                swap(a[i-1],a[i]);
                break;
            }
        }
        cout<<a<<endl;
    }
}
 
int main(){
    int _;
    cin>>_;
    while(_--){
        solve();
    }
    return 0;
}

C题：

解答：

存在一条边：较大点大于等于另外一条边的较大点，较小点也比大于等于另外一条边的较小点，且另外一条边的较大点大于等于这条边的较小点。

#include<bits/stdc++.h>
using namespace std;
 
void solve(){
    vector<pair<int,int>>arr(2);
    for(int i=0,x,d;i<2;i++){
        cin>>x>>d;
        arr[i]={max(x,d),min(x,d)};
    }
    sort(arr.begin(),arr.end());
 
    if(arr[1].second>=arr[0].second&&arr[0].first>=arr[1].second)cout<<"YES"<<endl;
    else cout<<"NO"<<endl;
}
 
int main(){
    int _;
    cin>>_;
    while(_--){
        solve();
    }
    return 0;
}

D题：

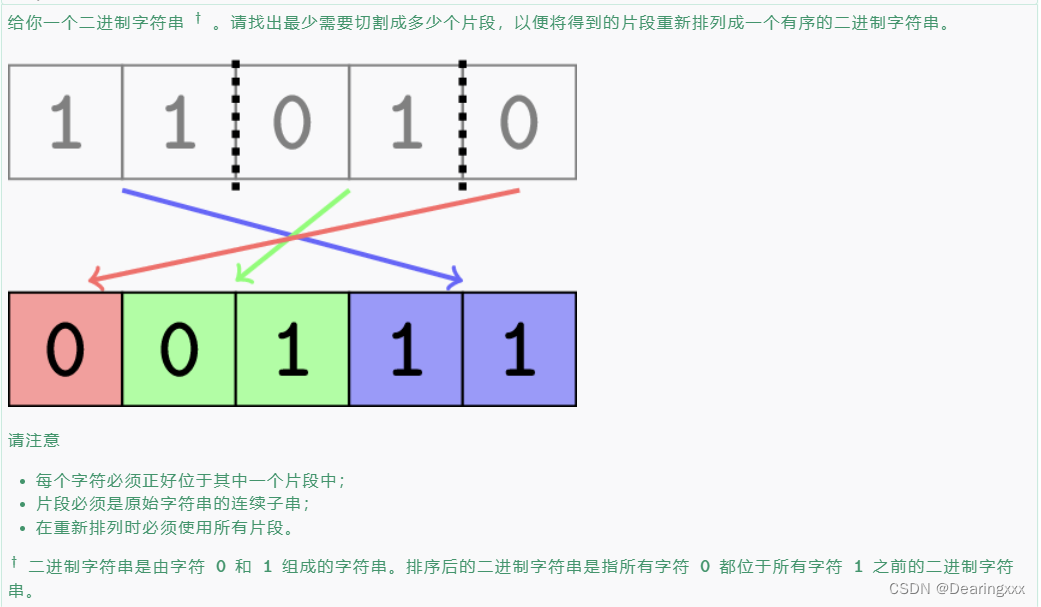
解答：

将连续0片段和连续1片段都剪出来，在把0和1拼在一起，但可以有一个~01~片段最为0和1的连接，所以剪的总段数减去这个~01~片段的贡献度。

#include<bits/stdc++.h>
using namespace std;
 
void solve(){
    string a;
    cin>>a;
    char w=a[0];
    int ans=1;
    int flag=0;
    for(int i=1;i<a.size();i++){
        if(a[i]!=w){
            ans++;
            w=a[i];
        }
        if(a[i-1]=='0'&&a[i]=='1')flag=1;
    }
    cout<<ans-flag<<endl;
}
 
int main(){
    int _;
    cin>>_;
    while(_--){
        solve();
    }
    return 0;
}

E题：

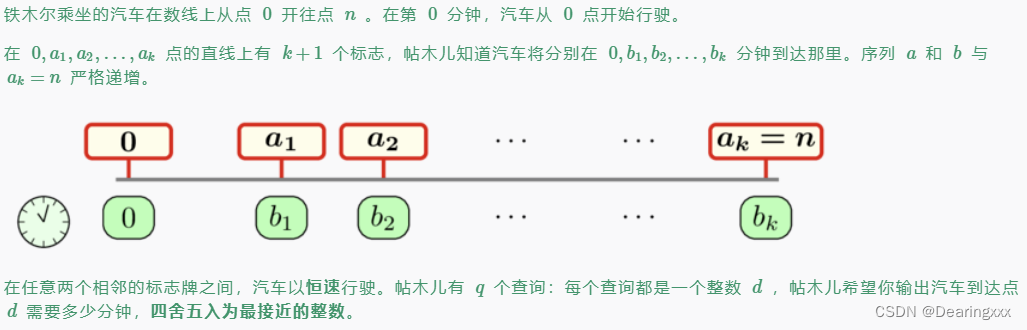
解答：

因为终点一定有一个标志，根据查询的距离，需要计算的只是当前距离刚好处在的区间，而已经走过的区间时间是固定的，所以只需要用一个01二分查询到所处的区间，并计算在当前区间所用的时间加上已走过区间即可。

#include<bits/stdc++.h>
using namespace std;
#define int long long
//二分查找函数传入数组必须用引用的方式，不然会增加一个传参的复杂度O(n),容易导致超时
int bf(vector<pair<int,int>>&arr,int x){
    int l=0,r=arr.size()-1,mid;
    while(l<r){
        mid=(l+r)>>1;
        if(arr[mid].first>=x)r=mid;
        else l=mid+1;
    }
    return r;
}
 
void solve(){
    int n,k,q;
    cin>>n>>k>>q;
    vector<pair<int,int> >arr(k);
    for(int i=0,a;i<k;i++){
        cin>>a;
        arr[i]={a,0};
    }
    for(int i=0,a;i<k;i++){
        cin>>a;
        arr[i]={arr[i].first,a};
    }
    for(int i=0;i<q;i++){
        int a;
        cin>>a;
        int ind=bf(arr,a);
        if(ind==0){
            //不引入浮点数实现结果舍去小数
            cout<<(int)((arr[0].second*a/arr[0].first))<<" ";
        }else{
            //不引入浮点数实现结果舍去小数
            cout<<(int)(arr[ind-1].second+((arr[ind].second-arr[ind-1].second)*(a-arr[ind-1].first)/(arr[ind].first-arr[ind-1].first)))<<" ";
        }
    }
    cout<<endl;
}
 
signed main(){
    ios::sync_with_stdio(0);
    cout.tie(0);
    cin.tie(0);
    int _;
    cin>>_;
    while(_--){
        solve();
    }
    return 0;
}

复盘所获：

1.此题结果要求舍去小数，又因为运算过程中区间的速度为一个浮点数是有必要的，但如果在运算过程中引入浮点数，可能会来带精度损失被Hack，所以一种可行的解决办法是将一次性把乘法算完再进行除法运算。

2.向二分查找函数中传递数组的时候必须使用引用的方式，不然会增加一个传递参数的复杂度O(n)，导致超时

F题：

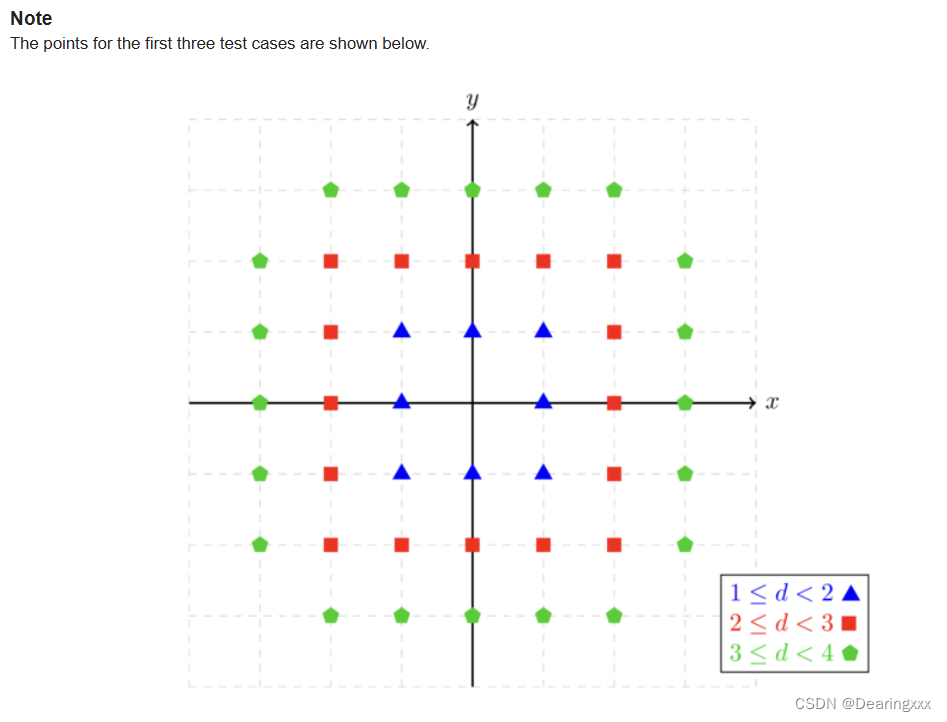
解答：
因为均匀分布在4个象限，所以将其中一个象限的点数乘4即是最后答案。

一种可行的解答方案是：枚举x(1<=x<=r)的值根据条件的变式,计算每一个x对应的y的数量即为该x值下对应的点的数量max-min+1，注意距离严格小于r+1，所以需要对进行特判，如果它是完全平方数需要再在结果上减一。

#include<bits/stdc++.h>
using namespace std;
#define int long long
//判断是否是一个完全平方数
bool is(int x){
    int xx=sqrt(x);
    return xx*xx==x;
}
 
 
void solve(){
    int n;
    cin>>n;
    int un=(int)pow(n+1,2);
    int dn=(int)pow(n,2);
    int sum=0;
    for(int i=1;i<=n;i++){
        int up=un-(int)pow(i,2);
        int down=dn-(int)pow(i,2);
        int tag=is(up);
        sum+=floor(sqrt(up))-ceil(sqrt(down))+1-tag;
        
    }
    cout<<sum*4<<endl;
}
 
signed main(){
    int _;
    cin>>_;
    while(_--){
        solve();
    }
    return 0;
}

复盘所获：

模板：是否是完全平方数

bool is(int x){
    int xx=sqrt(x);
    return xx*xx==x;
}

G题：

解答：

能够发生交换的ai和aj已经进行了限定只有ai XOR aj < 4之间的元素间可以交换，ai XOR aj < 4代表ai和aj二进制位只有后两位不同其他位相同，可以把只有后两位不同的数看成一个种类，无论数组中元素交换到什么位置，相互交换都只发生在同一种类中，所以只需要所有元素在输出时按要求分好种类，再在每个种类内部进行排序，输出时根据原本位置上数所属的种类依次从小到大输出对应种类内部排好序的元素即可。

#include<bits/stdc++.h>
using namespace std;
#define int long long
 
void solve(){
    int n;
    cin>>n;
    vector<int>arr(n);
    map<int,multiset<int>>m;
    for(int i=0;i<n;i++){
        cin>>arr[i];
        m[arr[i]>>2].insert(arr[i]);
    }
    for(int i=0;i<n;i++){
        cout<<*m[arr[i]>>2].begin()<<" ";
        m[arr[i]>>2].erase(m[arr[i]>>2].begin());
    }
    cout<<endl;
}
 
signed main(){
    int _;
    cin>>_;
    while(_--){
        solve();
    }
    return 0;
}

复盘所获：

向set中