LeetCode 题解随笔：图论（一）_vectorgraph

目录

零、前言

一、图的遍历

797. 所有可能的路径

二、拓扑排序问题

 1、环检测算法（DFS）

207. 课程表

 2、拓扑排序算法

210. 课程表 II[*]

三、二分图

 785. 判断二分图

886. 可能的二分法

四、最小生成树

1、Kruskal算法

 1584. 连接所有点的最小费用

2、Prim算法

---

零、前言

常用邻接表和邻接矩阵来实现图，如下图所示（来源：labuladong）

// 邻接表
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;
 
// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;

 邻接表好处是占用的空间少，但是邻接表无法快速判断两个节点是否相邻。

图和多叉树最大的区别是，图是可能包含环的，从图的某一个节点开始遍历，有可能走了一圈又回到这个节点，而树不会出现这种情况。所以，遍历框架需要一个 visited 数组进行辅助：

// 记录被遍历过的节点
boolean[] visited;
// 记录从起点到当前节点的路径
boolean[] onPath;
 
/* 图遍历框架 */
void traverse(Graph graph, int s) {
    if (visited[s]) return;
    // 经过节点 s，标记为已遍历
    visited[s] = true;
    // 做选择：标记节点 s 在路径上
    onPath[s] = true;
    for (int neighbor : graph.neighbors(s)) {
        traverse(graph, neighbor);
    }
    // 撤销选择：节点 s 离开路径
    onPath[s] = false;

 如果要处理路径相关的问题，这个 onPath 变量是肯定会被用到的，类似回溯法过程中的标记。 

---

一、图的遍历

797. 所有可能的路径

vector<int> path;
    vector<vector<int>> res;
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        // 找出所有从节点 0 到节点 n-1 的路径。起点一定是结点0
        path.push_back(0);
        Traversal(graph, 0);
        return res;
    }
    void Traversal(vector<vector<int>>& graph, int cur_node) {  
        // 到节点 n-1才能记录结果
        if (cur_node == graph.size() - 1) {
            res.push_back(path);      
            return;
        }
        for (auto next_node : graph[cur_node]) {
            path.push_back(next_node);
            Traversal(graph, next_node);
            path.pop_back();
        }
    }

由于是无环图，不需要visited数组。

---

二、拓扑排序问题

 1、环检测算法（DFS）

207. 课程表

看到依赖问题，首先想到的就是把问题转化成「有向图」这种数据结构，只要图中存在环，那就说明存在循环依赖。

 首先利用邻接表的方式建图：

vector<vector<int>> BuildGraph(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> graph;
        graph.resize(numCourses);
        for (auto courses : prerequisites) {
            graph[courses[1]].push_back(courses[0]);
        }
        return graph;
    }

 利用path数组记录当前递归栈中的元素，即当前所保存的路径；在利用一个visited数组记录遍历过的结点，防止走回头路。

类比贪吃蛇游戏，visited 记录蛇经过过的格子，而 onPath 仅仅记录蛇身。onPath 用于判断是否成环，类比当贪吃蛇自己咬到自己（成环）的场景。

vector<bool> onPath;
    vector<bool> visited;
    bool hasCycle;
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        hasCycle = false;
        vector<vector<int>> graph = BuildGraph(numCourses, prerequisites);
        onPath.resize(graph.size(), false);
        visited.resize(graph.size(), false);
        for (int i = 0; i < numCourses; i++) {
            Traversal(graph, i);
        }
        return !hasCycle;
    }
    vector<vector<int>> BuildGraph(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> graph;
        graph.resize(numCourses);
        for (auto courses : prerequisites) {
            graph[courses[1]].push_back(courses[0]);
        }
        return graph;
    }
    void Traversal(vector<vector<int>>& graph, int course) {
        // 出现环
        if (onPath[course])  hasCycle = true;
        // 该结点已访问过 / 已经出现环，无需继续遍历
        if (visited[course] || hasCycle)    return;
        visited[course] = true;
        onPath[course] = true;
        for (auto next_course : graph[course]) {
            Traversal(graph, next_course);
        }
        onPath[course] = false;
    }

 2、拓扑排序算法

210. 课程表 II[*]

如果一幅图是「有向无环图」，那么一定可以进行拓扑排序。直观地说就是把一幅图「拉平」，而且这个「拉平」的图里面，所有箭头方向都是一致的。

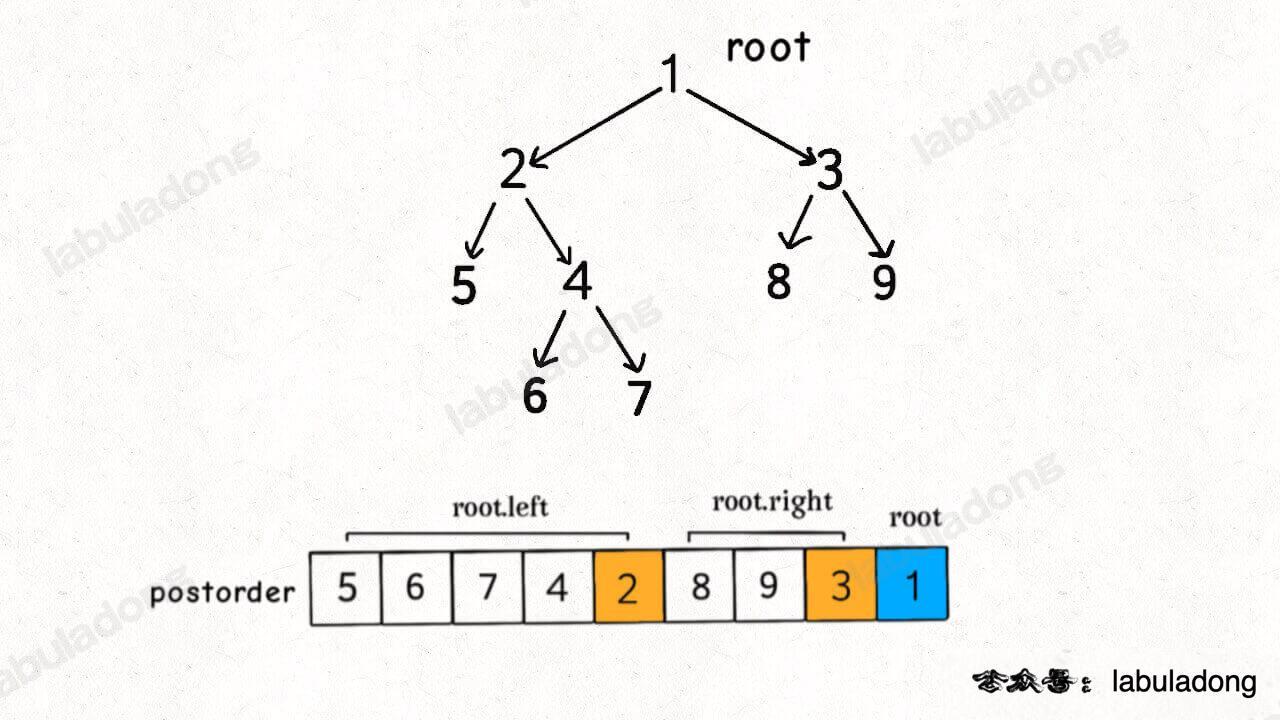
将后序遍历的结果进行反转，就是拓扑排序的结果。

vector<bool> onPath;
    vector<bool> visited;
    bool hasCycle;
    // 记录后序遍历结果
    vector<int> post_order;
    // 对于有向无环图，可以抽象成多叉树
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        if (!canFinish(numCourses, prerequisites))   return {};
        // 逆后序遍历结果即为拓扑排序结果
        reverse(post_order.begin(), post_order.end());
        return post_order;
    }
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        hasCycle = false;
        vector<vector<int>> graph = BuildGraph(numCourses, prerequisites);
        onPath.resize(graph.size(), false);
        visited.resize(graph.size(), false);
        for (int i = 0; i < numCourses; i++) {
            Traversal(graph, i);
        }
        return !hasCycle;
    }
    vector<vector<int>> BuildGraph(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> graph;
        graph.resize(numCourses);
        for (auto courses : prerequisites) {
            graph[courses[1]].push_back(courses[0]);
        }
        return graph;
    }
    void Traversal(vector<vector<int>>& graph, int course) {
        // 出现环
        if (onPath[course])  hasCycle = true;
        // 该结点已访问过 / 已经出现环，无需继续遍历
        if (visited[course] || hasCycle)    return;
        // 前序遍历位置
        visited[course] = true;
        onPath[course] = true;
        for (auto next_course : graph[course]) {
            Traversal(graph, next_course);
        }
        // 后序遍历位置
        post_order.push_back(course);
        onPath[course] = false;
    }

 之所以拓扑排序的基础是后序遍历，是因为一个任务必须等到它依赖的所有任务都完成之后才能开始开始执行。抽象多叉树结构中，边的含义即是「被依赖」关系。（来源：labuladong）

---

三、二分图

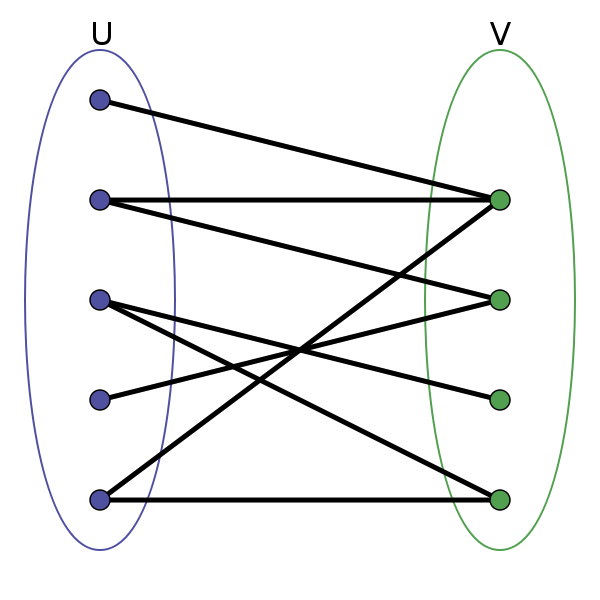
二分图的顶点集可分割为两个互不相交的子集，图中每条边依附的两个顶点都分属于这两个子集，且两个子集内的顶点不相邻。

应用：电影和演员之间的相互映射

二分图的判断（遍历）逻辑：

/* 图遍历框架 */
void traverse(Graph graph, boolean[] visited, int v) {
    visited[v] = true;
    // 遍历节点 v 的所有相邻节点 neighbor
    for (int neighbor : graph.neighbors(v)) {
        if (!visited[neighbor]) {
            // 相邻节点 neighbor 没有被访问过
            // 那么应该给节点 neighbor 涂上和节点 v 不同的颜色
            traverse(graph, visited, neighbor);
        } else {
            // 相邻节点 neighbor 已经被访问过
            // 那么应该比较节点 neighbor 和节点 v 的颜色
            // 若相同，则此图不是二分图
        }
    }
}

 785. 判断二分图

// 记录图中节点是否被访问过
    vector<bool> visited;
    // 记录图中节点的颜色，false 和 true 代表两种不同颜色
    vector<bool> color;
    bool res = true;
    bool isBipartite(vector<vector<int>>& graph) {
        visited.resize(graph.size());
        color.resize(graph.size(), false);
        // 因为图不一定是联通的，可能存在多个子图
        // 所以要把每个节点都作为起点进行一次遍历
        // 如果发现任何一个子图不是二分图，整幅图都不算二分图
        for (int i = 0; i < graph.size(); i++) {
            if (!visited[i]) {
                Traversal(graph, i);
            }
        }
        Traversal(graph, 0);
        return res;
    }
    void Traversal(vector<vector<int>>& graph, int v) {
        if (!res)    return;
        visited[v] = true;
        for (auto neighber : graph[v]) {
            // 相邻节点 w 没有被访问过
            // 那么应该给节点 w 涂上和节点 v 不同的颜色
            if (!visited[neighber]) {
                color[neighber] = !color[v];
                Traversal(graph, neighber);
            }
            // 相邻节点 w 已经被访问过
            // 根据 v 和 w 的颜色判断是否是二分图
            else {
                if (color[neighber] == color[v])    res = false;
            }
        }
    }

 注意：由于图可能不连通，要从把每个节点都作为起始节点将图遍历一遍（有visited数组，可以避免重复遍历）。

886. 可能的二分法

vector<bool> visited;
    vector<bool> group;
    bool res = true;
    bool possibleBipartition(int n, vector<vector<int>>& dislikes) {
        visited.resize(n + 1);
        group.resize(n + 1);
        vector<vector<int>> graph = BuildGraph(dislikes, n);
        for (int i = 1; i <= n; ++i) {
            if (!visited[i]) {
                Traversal(graph, i);
            }
        }
        return res;
    }
    void Traversal(vector<vector<int>>& graph, int person) {
        if (!res)    return;
        visited[person] = true;
        for (auto neighber : graph[person]) {
            if (!visited[neighber]) {
                group[neighber] = !group[person];
                Traversal(graph, neighber);
            }
            else {
                if (group[neighber] == group[person])   res = false;
            }
        }
    }
    vector<vector<int>> BuildGraph(vector<vector<int>>& dislikes, int n) {
        vector<vector<int>> graph;
        graph.resize(n + 1);
        for (auto dislike : dislikes) {
            // 「无向图」相当于「双向图」
            graph[dislike[0]].push_back(dislike[1]);
            graph[dislike[1]].push_back(dislike[0]);
        }
        return graph;
    }

如果你把每个人看做图中的节点，相互讨厌的关系看做图中的边，那么 dislikes 数组就可以构成一幅图。注意此处无向图可以当成双向图处理。 

---

四、最小生成树

1、Kruskal算法

 Union-Find 算法在 Kruskal 算法中的主要作用是保证最小生成树的合法性。因为在构造最小生成树的过程中，首先得保证生成的是棵树（不包含环）。

Kruskal 算法是一种常见并且好写的最小生成树算法。该算法的基本思想是从小到大加入边，是一个贪心算法。其算法流程为：

 1584. 连接所有点的最小费用

class Solution {
public:
    class UF {
    public:
        vector<int> father;
        // 并查集寻根：无根/递归找根
        int find(int u) {
            return u == father[u] ? u : father[u] = find(father[u]);
        }
        // 判断是否同根
        bool isSame(int u, int v) {
            u = find(u);
            v = find(v);
            return u == v;
        }
        // 将u -> v加入并查集
        void join(int u, int v) {
            u = find(u);
            v = find(v);
            if (u == v) return;
            father[u] = v;
        }
    };
 
    int minCostConnectPoints(vector<vector<int>>& points) {
        // edges记录了点i、点j两点的下标，及边(i,j)的长度
        vector<vector<int>> edges;
        for (int i = 0; i < points.size(); ++i) {
            for (int j = i + 1; j < points.size(); ++j) {
                int dist = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1]);
                edges.push_back({ i,j,dist });
            }
        }
        // 将边按照权值从小到大排序
        sort(edges.begin(), edges.end(), [](vector<int>& p1, vector<int>& p2) {return p1[2] < p2[2]; });
        // 使用并查集维护连通性，连通集中存储了点的下标
        UF uf;
        uf.father.resize(points.size());
        for (size_t i = 0; i < points.size(); ++i)   uf.father[i] = i;
        // 执行Kruskal算法
        int res = 0;
        int cur_edges = 0;
        for (auto edge : edges) {
            // 当前边的两端点不连通，则采用贪心原则，加入这条边
            if (!uf.isSame(edge[0], edge[1])) {
                uf.join(edge[0], edge[1]);
                ++cur_edges;
                res += edge[2];
                // 总边的个数等于点数减1
                if (cur_edges == points.size() - 1)    break;
            }
        }
        return res;
    }
};

2、Prim算法

首先，Prim 算法也使用贪心思想来让生成树的权重尽可能小，也就是「切分定理」。

 对于任意一种「切分」，其中权重最小的那条「横切边」一定是构成最小生成树的一条边。

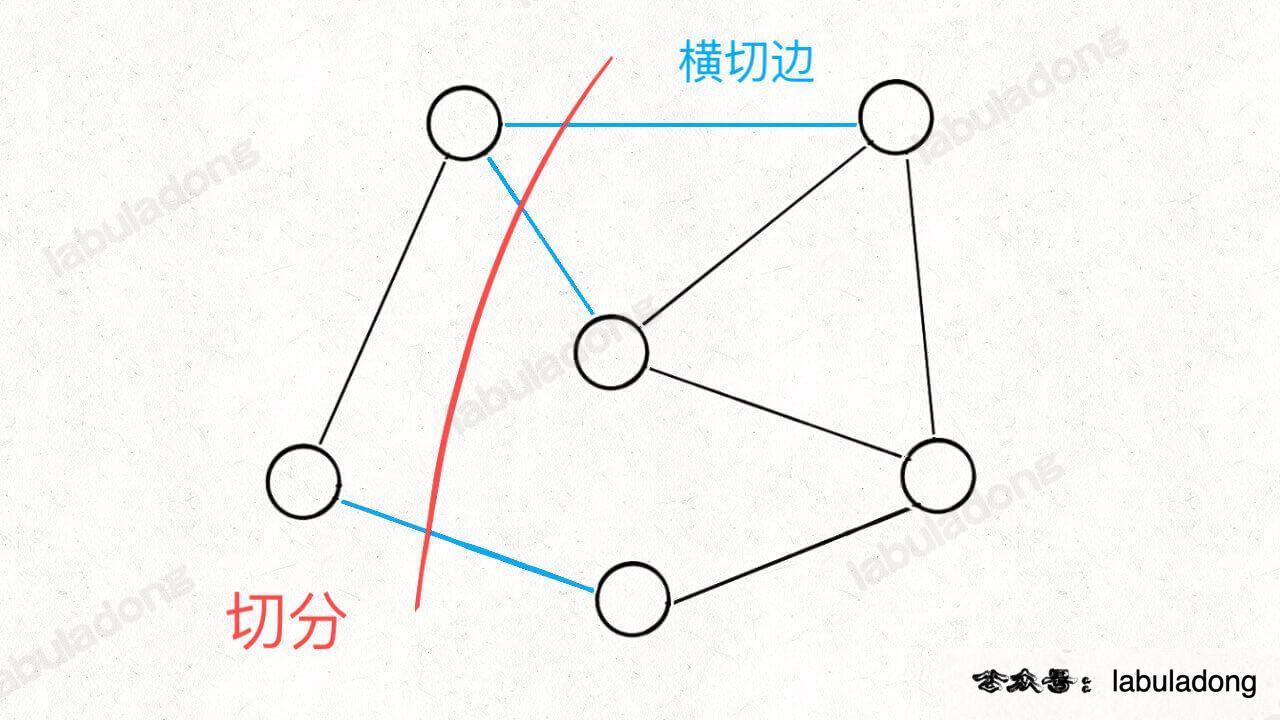
其次，Prim 算法使用 BFS 算法思想 和 visited 布尔数组避免成环，来保证选出来的边最终形成的一定是一棵树。（来源：labuladong）

核心思想：在进行切分的过程中，我们只要不断把新节点的邻边加入横切边集合，就可以得到新的切分的所有横切边。每次都把权重最小的「横切边」拿出来加入最小生成树，直到把构成最小生成树的所有边都切出来为止。

struct Edge {
        Edge(int p1, int p2, int distance) {
            point1 = p1;
            point2 = p2;
            cost = distance;
        }
        int point1;
        int point2;
        int cost;
    };
    int getCost(vector<int> point1, vector<int> point2) {
        return abs(point1[0] - point2[0]) + abs(point1[1] - point2[1]);
    }
    int minCostConnectPoints(vector<vector<int>>& points) {
        if (points.size() == 0) {
            return 0;
        }
        int size = points.size();
        priority_queue<Edge, vector<Edge>, cmp> pq; // 最小堆
        vector<bool> visited(size, false);
        int res = 0; // 总费用
        int cnt = size - 1; // 边数
        // 以0号顶点为起始点将0号点与其他点形成的边入队
        for (int i = 1; i < size; i++) {
            int cost = getCost(points[0], points[i]);
            Edge edge(0, i, cost);
            pq.push(edge);
        }
        visited[0] = true; // 标记0号点已访问
        while (!pq.empty() && cnt != 0) {
            auto edge = pq.top();
            pq.pop();
            if (visited[edge.point2]) { // 已访问的点形成的边不选取
                continue;
            }
            res += edge.cost;
            visited[edge.point2] = true;
            for (int i = 0; i < size; i++) {
                if (!visited[i]) {
                    int cost = getCost(points[edge.point2], points[i]);
                    Edge nextEdge(edge.point2, i, cost);
                    pq.push(nextEdge);
                }
            }
            cnt--;
        }
        return res;
    }
    struct cmp {
        bool operator() (Edge &a, Edge &b ) {
            return a.cost > b.cost;//最小堆
        }
    };

---

五、「加权图」中的最短路径问题（Dijkstra 算法）

Dijkstra 可以理解成一个带 dp table（或者说备忘录）的 BFS 算法。

743. 网络延迟时间

class Solution {
public:
    // 定义一个类，记录BFS遍历的层数【->针对最短路径问题，为start到当前结点的距离】
    class State {
    public:
        // 图节点的 id
        int id;
        // 从 start 节点到当前节点的距离
        int distFromStart;
        State(int id, int distFromStart) {
            this->id = id;
            this->distFromStart = distFromStart;
        }
    };
    struct MyCompare {
        bool operator()(State& s1, State& s2) {
            return s1.distFromStart > s2.distFromStart;
        }
    };
    // Dijkastra算法：输入一个起点 start，计算从 start 到其他节点的最短距离
    vector<int> Dijkastra(int start, vector<vector<vector<int>>>& graph) {
        // 定义：distTo[i] 的值就是起点 start 到达节点 i 的最短路径权重
        vector<int> res_dist(graph.size(), 999);
        // base case，start 到 start 的最短距离就是 0
        res_dist[start] = 0;
 
        // 优先级队列，最小堆，distFromStart 较小的排在前面
        priority_queue<State, vector<State>, MyCompare> pq;
        // 从起点 start 开始进行 BFS
        pq.push(State(start, 0));
        while (!pq.empty()) {
            State cur_state = pq.top();
            int cur_id = cur_state.id;
            int cur_distFromStart = cur_state.distFromStart;
            pq.pop();
            // 已经有一条更短的路径到达 curNode 节点了
            if (cur_distFromStart > res_dist[cur_id]) {
                continue;
            }
            // 将 curNode 的【能使距离减小的】相邻节点装入队列
            for (auto nextNode : graph[cur_id]) {
                int dist_to_next_node = res_dist[cur_id] + nextNode[1];
                if (res_dist[nextNode[0]] > dist_to_next_node) {
                    // 更新 dp table
                    res_dist[nextNode[0]] = dist_to_next_node;
                    // 将这个节点以及距离放入队列
                    pq.push(State(nextNode[0], dist_to_next_node));
                }
            }
        }
        return res_dist;
    }
   vector<vector<vector<int>>> BuildGraph(vector<vector<int>>& times, int n) {
        vector<vector<vector<int>>> graph;
        graph.resize(n);
        for (auto time : times) {
            graph[time[0]].push_back({ time[1],time[2] });
        }
        return graph;
    }
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        // 网络节点标记为 1 到 n
        auto graph = BuildGraph(times, n + 1);
        vector<int> time_each_point = Dijkastra(k, graph);
        int res = 0;
        for (size_t i = 1; i <= n; ++i) {
            if (time_each_point[i] == 999) {
                // 有节点不可达，返回 -1
                return -1;
            }
            res = *max_element(++time_each_point.begin(), time_each_point.end());
        }
        return res;
    }
};