人工智能学习(七):概率_概率的归一性
赞
踩
目录
7.1.3 联合分布(Joint Distributions)
7.1.6 边际分布(Marginal Disttibutions)
7.1 不确定性(Uncertainty)
一般情况下:
这里的模型也是变量的集合,但它们是随机变量,有时我们知道它们的值,有时不知道。当我们知道它的取值时,这个变量就是证据。另外一些我们不知道值得变量就是未被观察到得变量。
- 观察到的变量(证据):代理知道关于世界状态的某些事情(例如,传感器读数或症状)。
- 未观察到的变量:代理需要对其他方面进行推理(例如,物体在哪里或存在什么疾病)。
- 模型:代理知道一些关于已知变量与未知变量的关系。
概率推理给了我们一个管理信念度和知识的框架。
7.1.1 随机变量
随机变量是世界上我们(可能)不确定的一些方面。
用大写字母表示一个随机变量,例如:
随机变量有自己的域,例如:。
7.1.2 概率分布
将概率与数值联系起来:
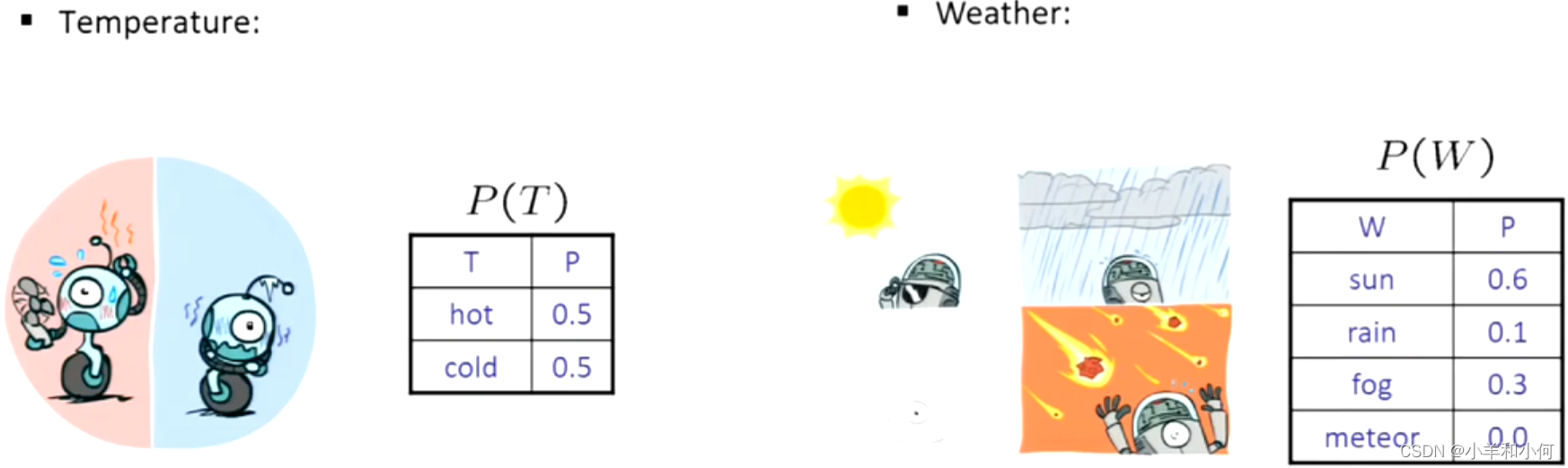
在真实的模型中,零是一个很大的禁忌,我们应该用一个比其他概率都小的多的数代替它。
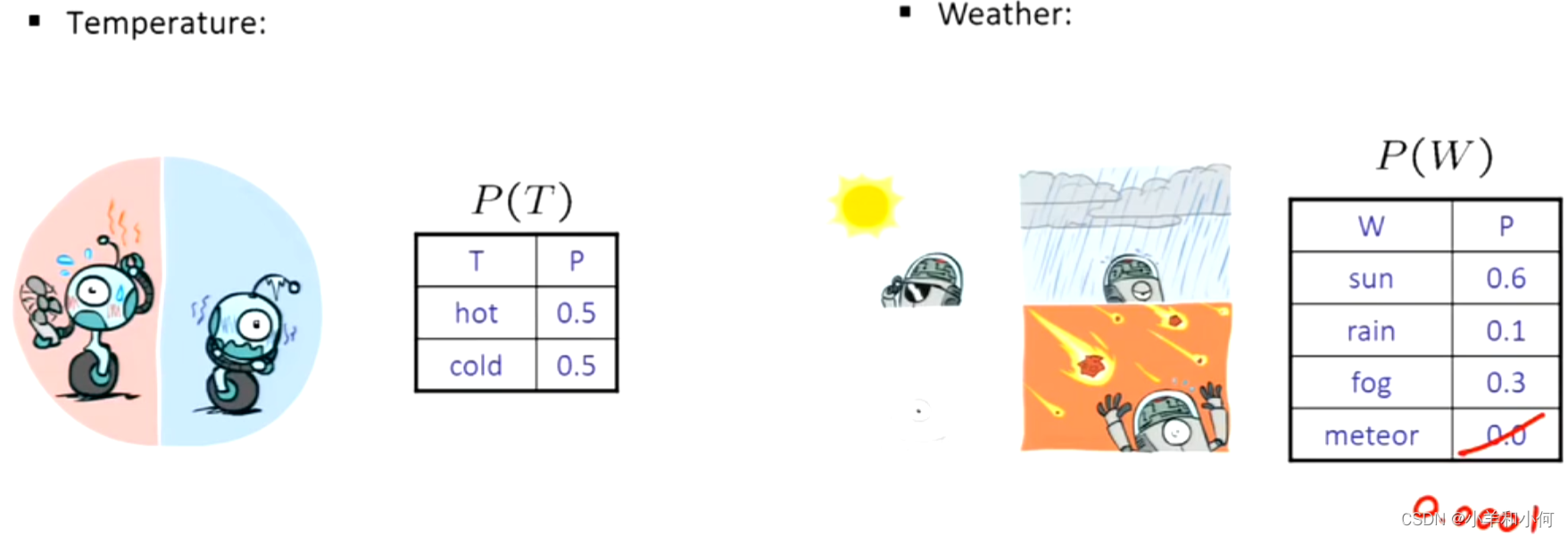
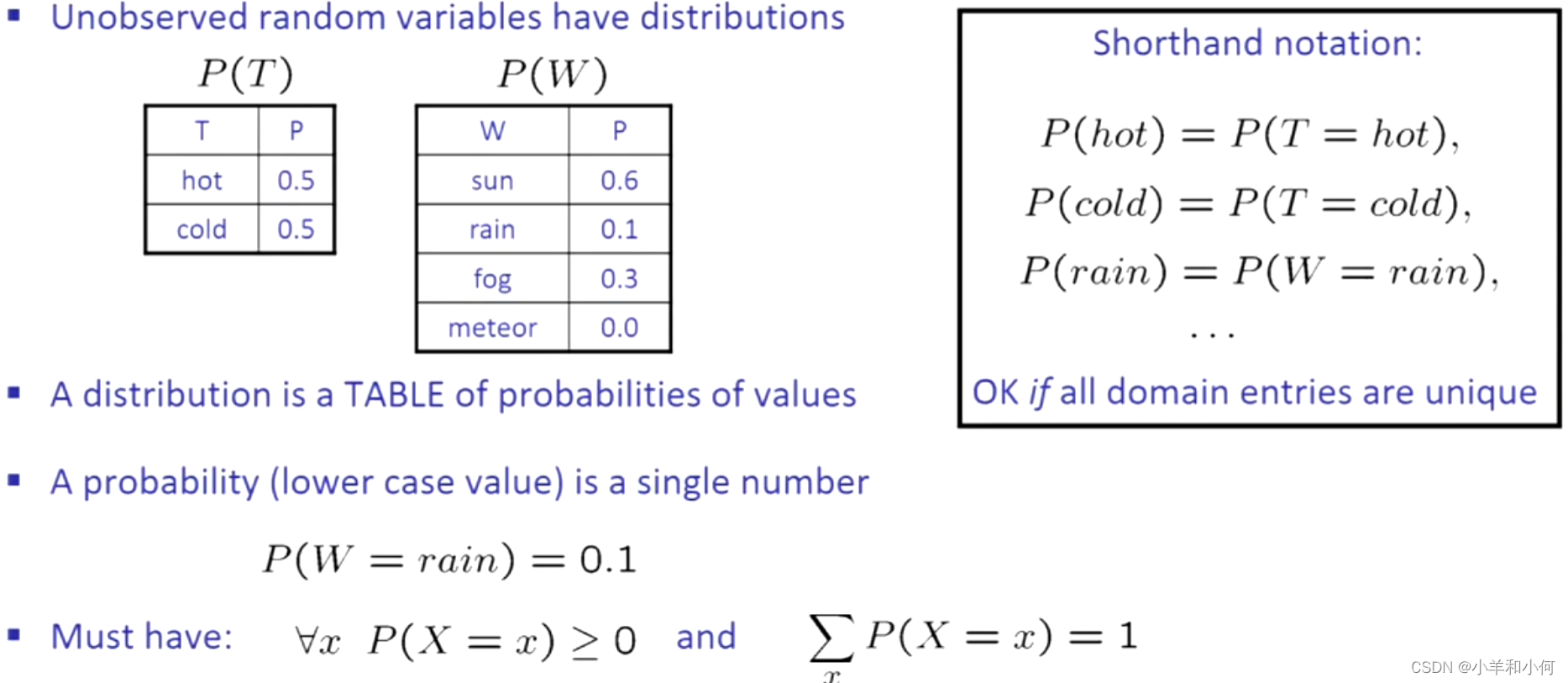
必须有对于任意的取值,
,并且变量所有取值的概率总和为
。
7.1.3 联合分布(Joint Distributions)
联合分布就类似于搜索空间,拥有它我们可以做概率下的任何事情,但是它往往过于庞大。
一组随机变量的联合分布:,为每个分配(或结果)指定一个实数:
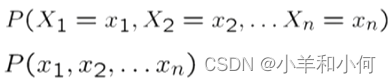
有了联合概率分布表,我们可以求算想要的任何派升值。
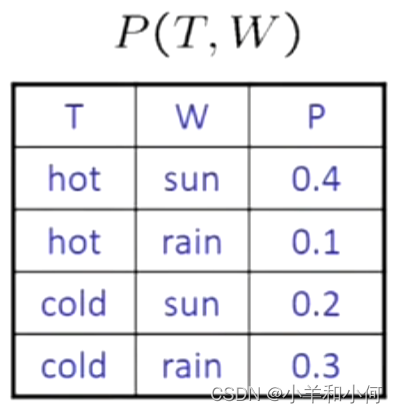
联合概率有要遵循的规则,但规则是松散的:
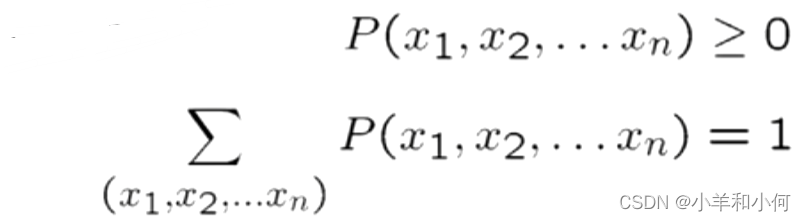
联合概率分布表是很好的,但往往受限于它的大小。假设有个变量,每个变量有
个值:
。
7.1.4 概率模型
一个概率模型是一组随机变量的联合分布。
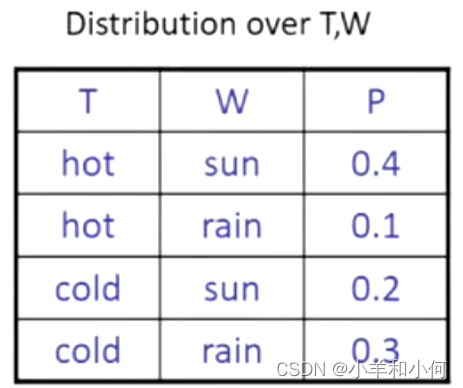
概率模型:
- 有域的(随机)变量。
被称为
。
- 联合分布:说明
(
)是否可能出现。
- 归一化:总和为
- 理想情况下:只有某些变量直接互动。
和问题的区别:
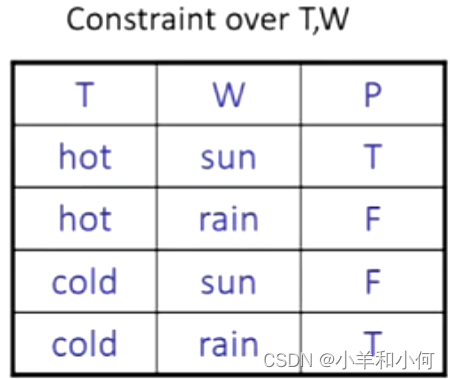
限制性满足问题:
- 带域的变量。
- 约束:说明赋值是否可行。
- 理想情况下:只有某些变量直接互动。
概率模型中的变量和上这些相同变量上的区别是什么?它们确实比较相似,
可以被认为是一个巨人,指定了一个巨大的真值表,
代表变量的取值符合约束,
代表变量的取值违反了约束。
7.1.5 事件
一个事件是一组的
。
![]()
从联合分布中,我们可以计算出任何事件的概率。
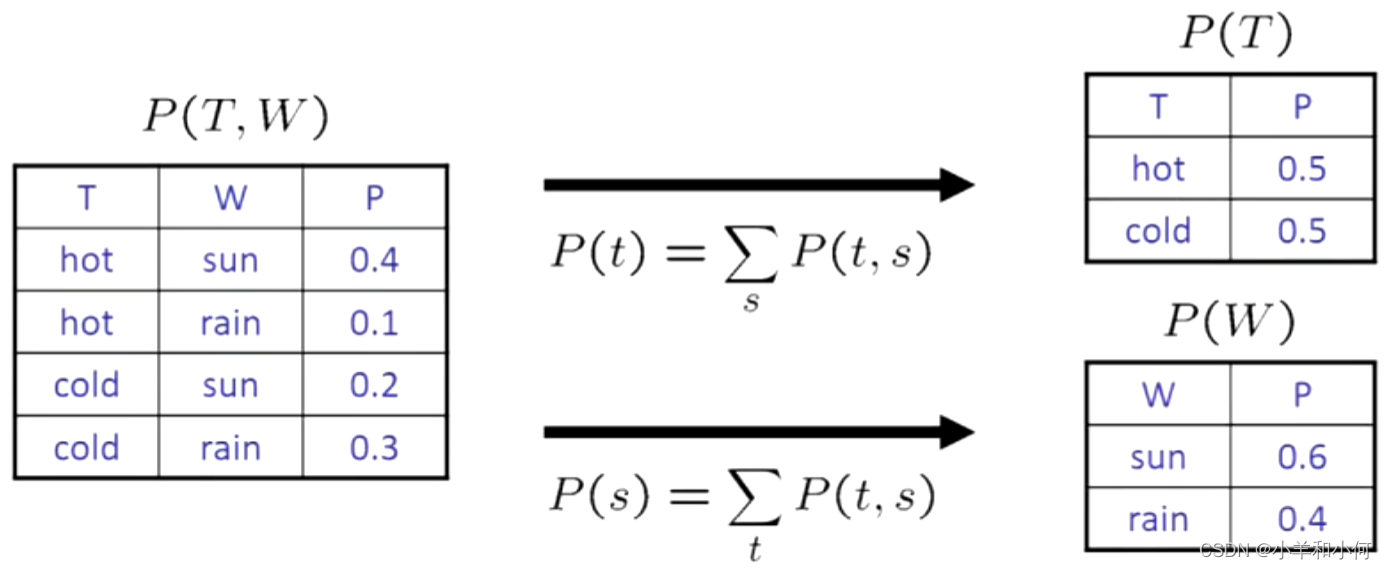
7.1.6 边际分布(Marginal Disttibutions)
边际分布是一个子表,消除变量的子表。
边际化(求和):通过加法将折叠的行合并起来。
7.1.7 条件概率
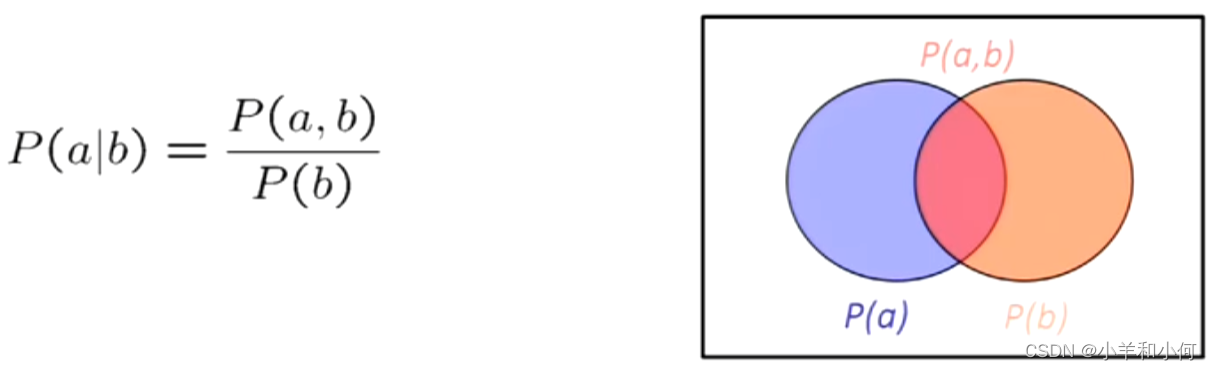
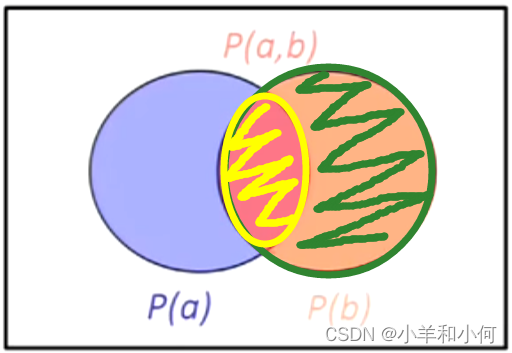
联合概率和条件概率之间的简单关系:
事实上,这被当作是条件概率的定义
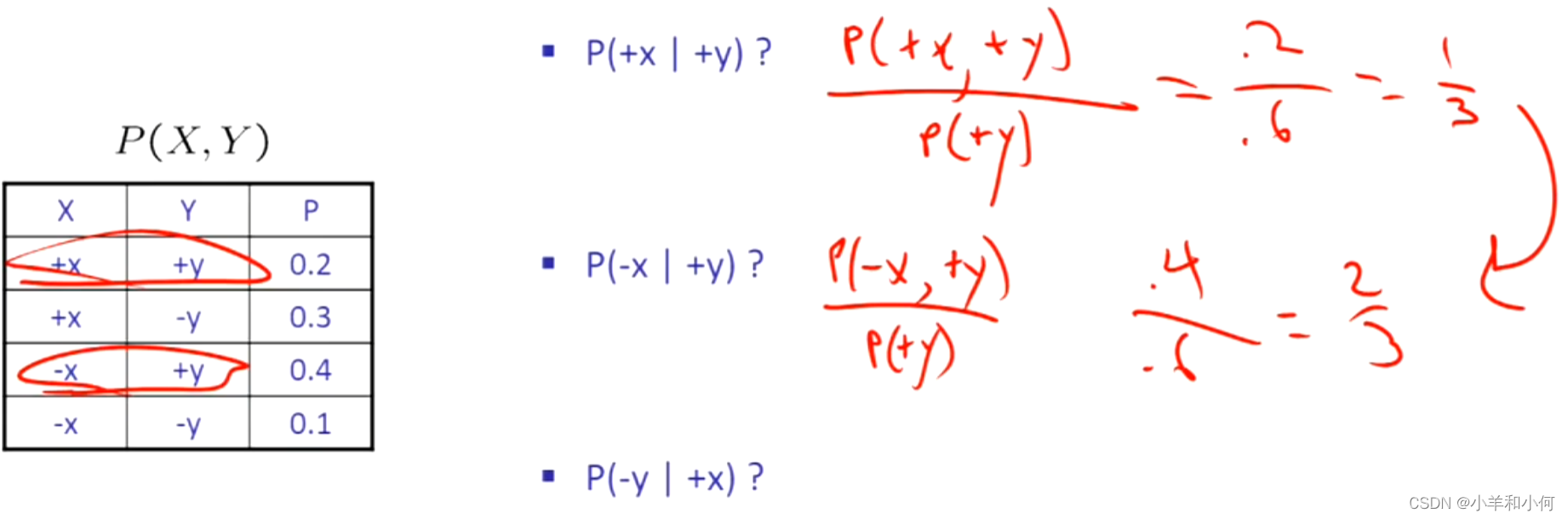
7.1.8 条件分布
条件分布是在给定其他变量的固定值的情况下,某些变量的概率分布。
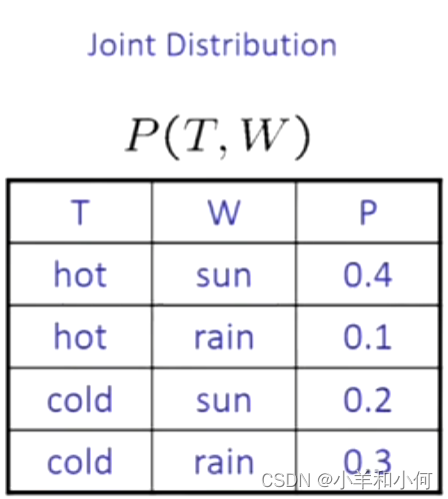
条件分布:


条件分布和边际分布不同,因为条件是基于证据的,什么是证据,之前讲过证据就是随机变量的真实取值。
7.1.9 归一化技巧
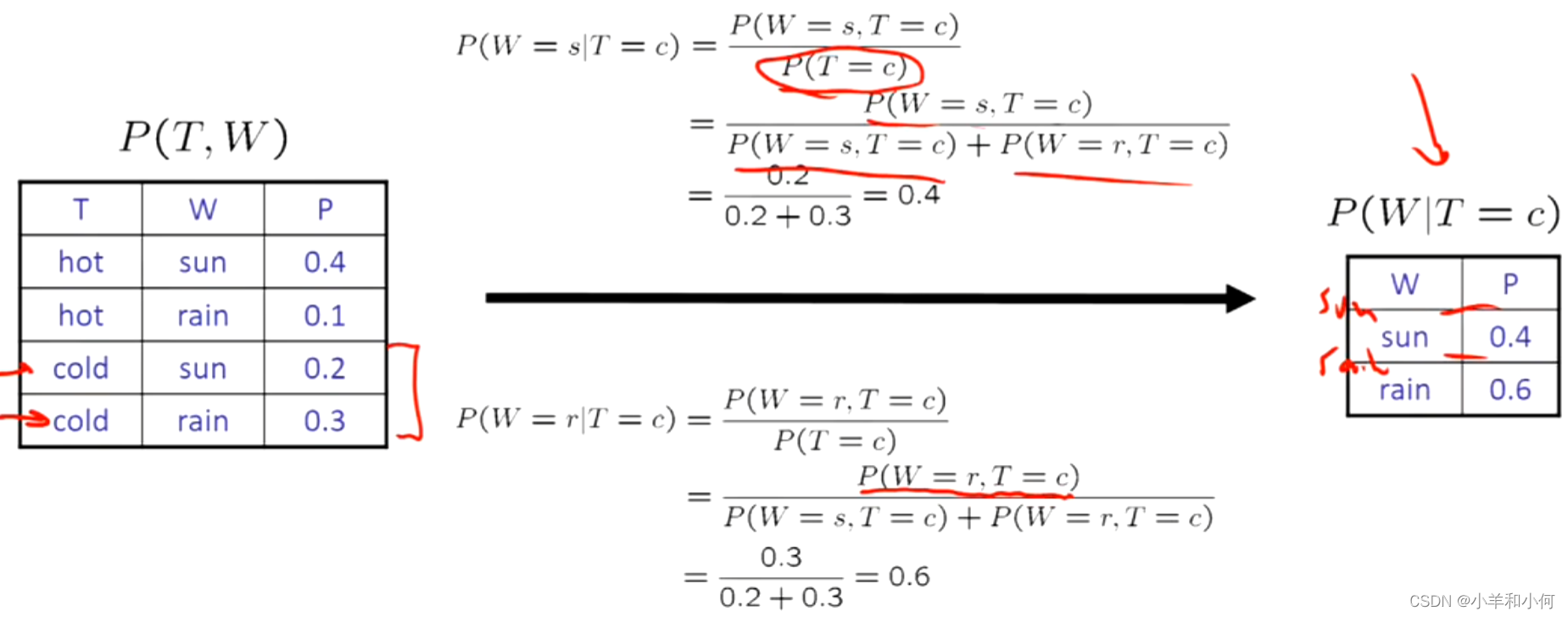
要想计算条件分布,快速的思考方式是直接进行归一化。
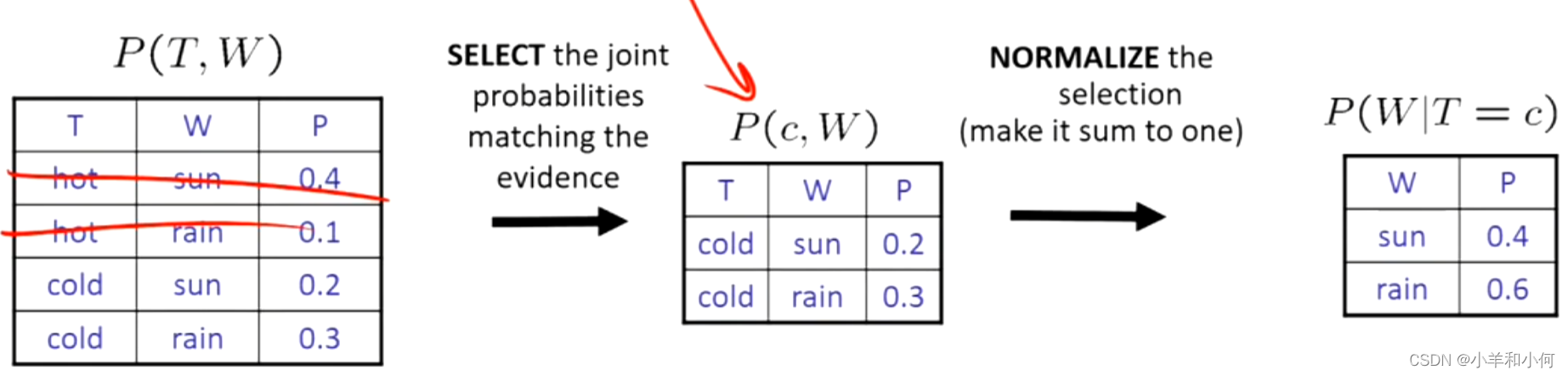
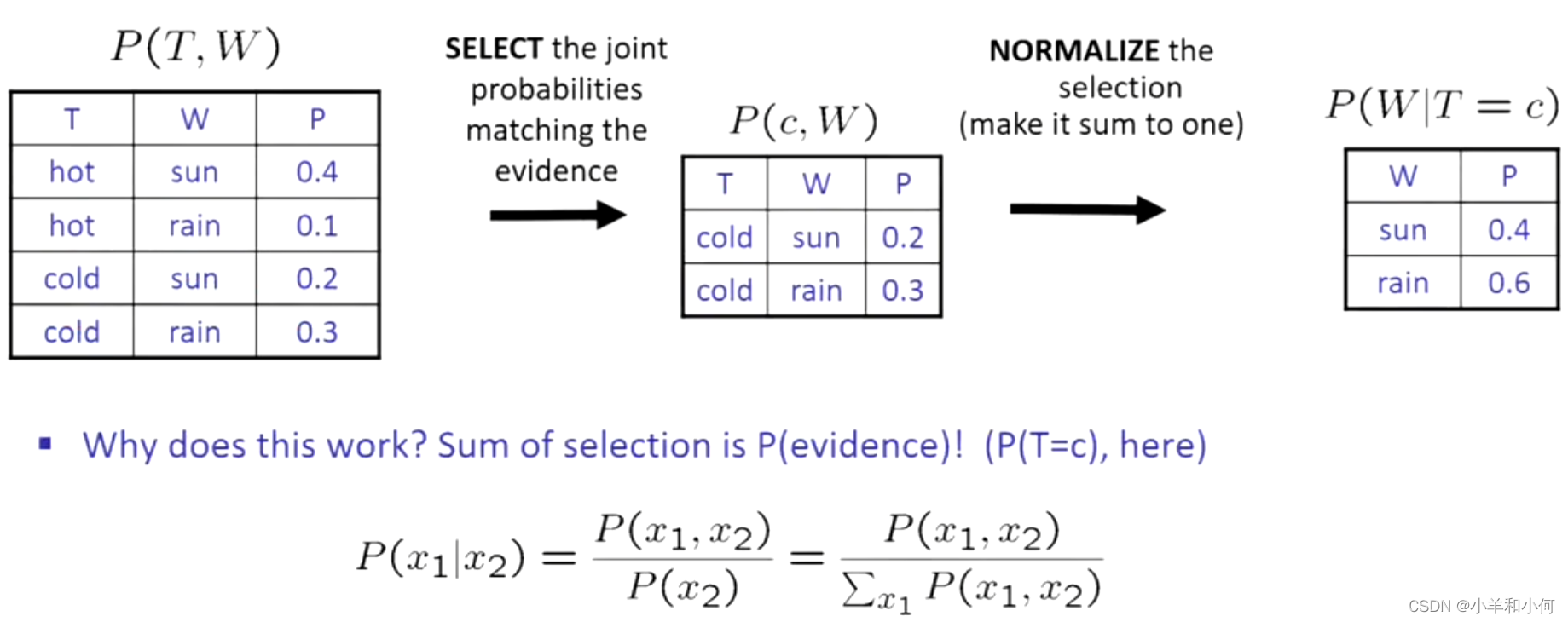
7.1.10 归一化

7.2 概率论推理
概率推理:
从其他已知的概率中计算出一个期望的概率(例如,从联合概率中计算出条件概率)。
我们通常计算条件概率
- 这些代表了代理对证据的看法。
概率随着新证据的出现而变化。
- 观察到新的证据会导致信念的更新。
7.2.1 通过枚举进行推理
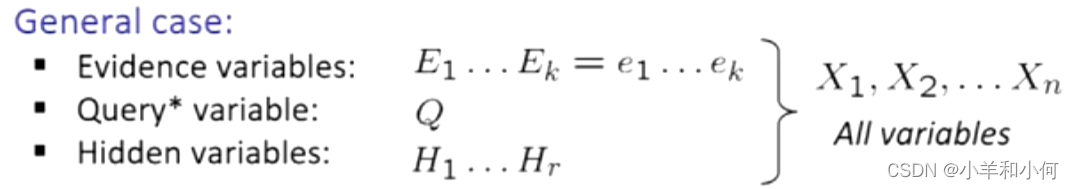
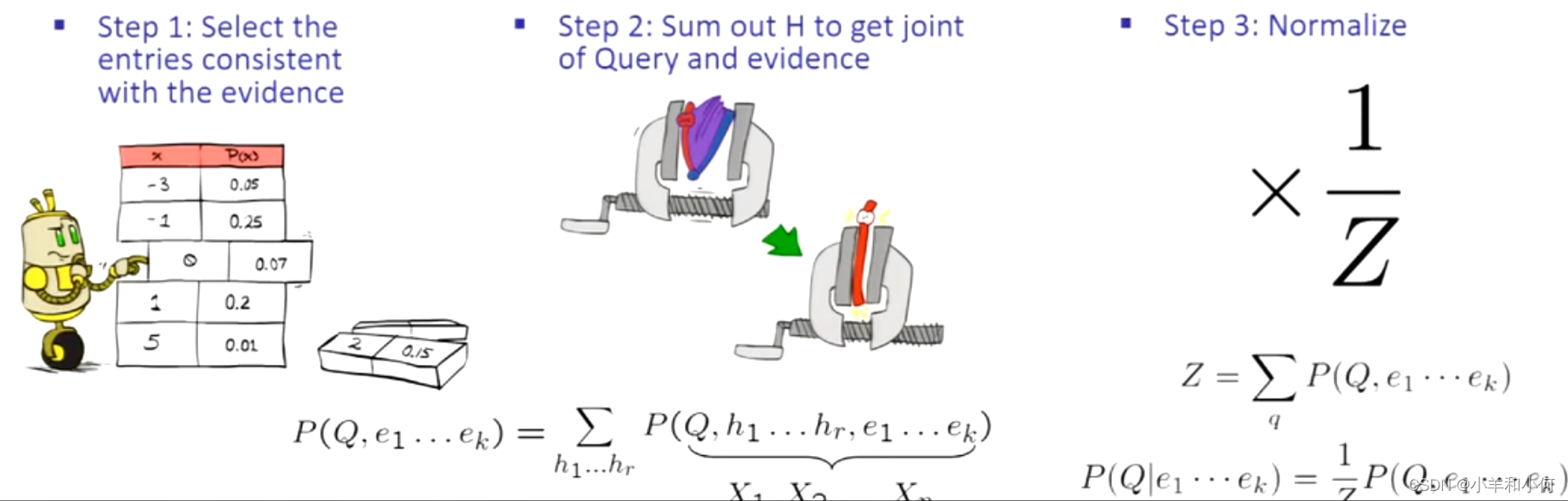
取得整个分布,选择与我的证据一致的东西。折叠我不关心的变量,只剩下你想查询的维度。最后正则化。
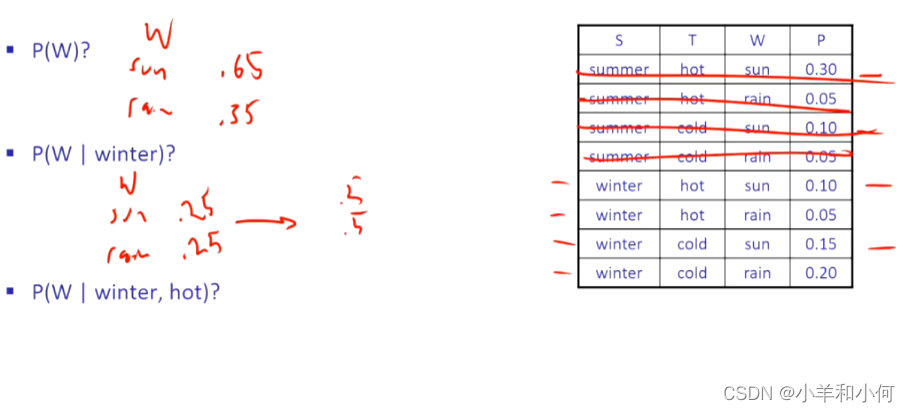
例子:
和
是隐藏变量:

变成了证据,
是隐藏变量:
和
都变成了证据:
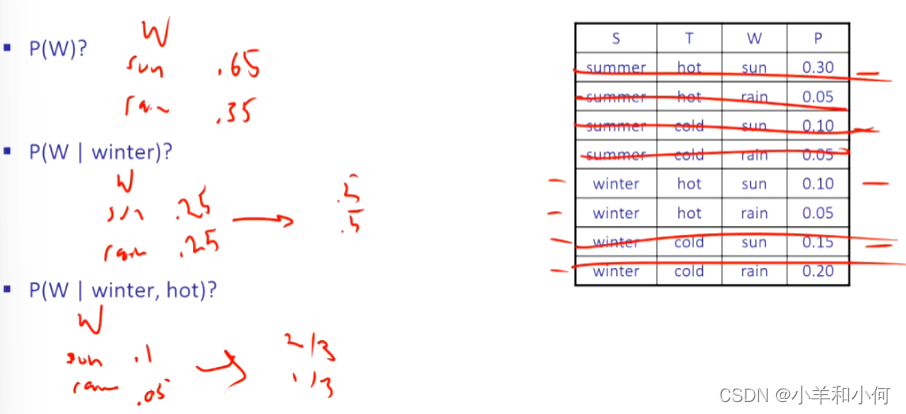
真正有用的就是这些条件分布,在一定证据下的变量概率。
使用枚举推理的明显问题:
- 最坏情况下的时间复杂度为
。
- 存储联合分布的空间复杂度为
。
7.3 计算概率的工具
有时我们有条件分布,但想要联合分布:
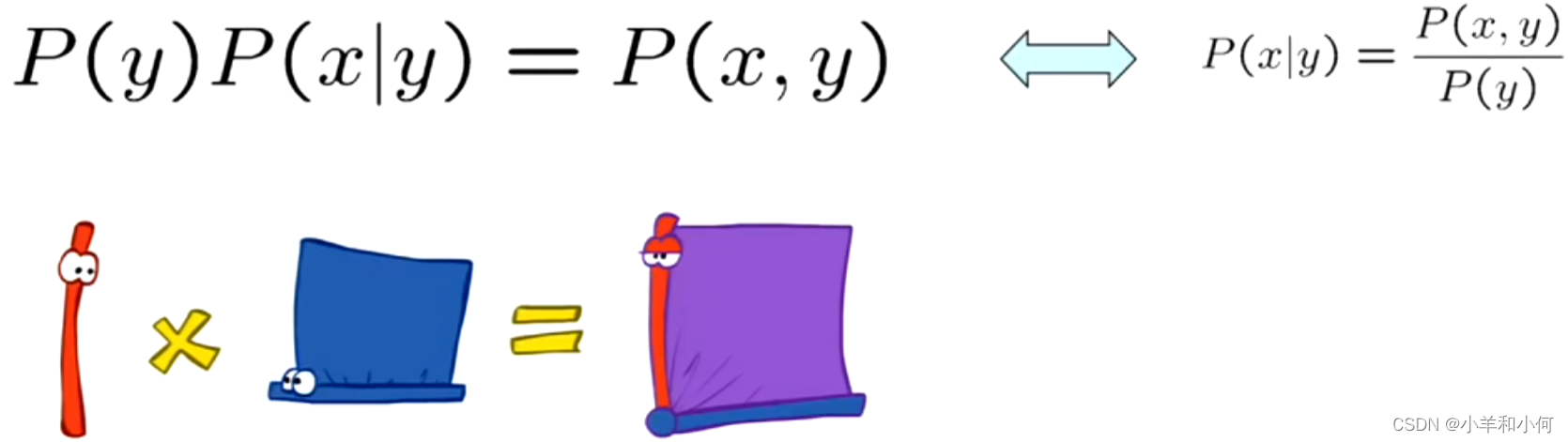
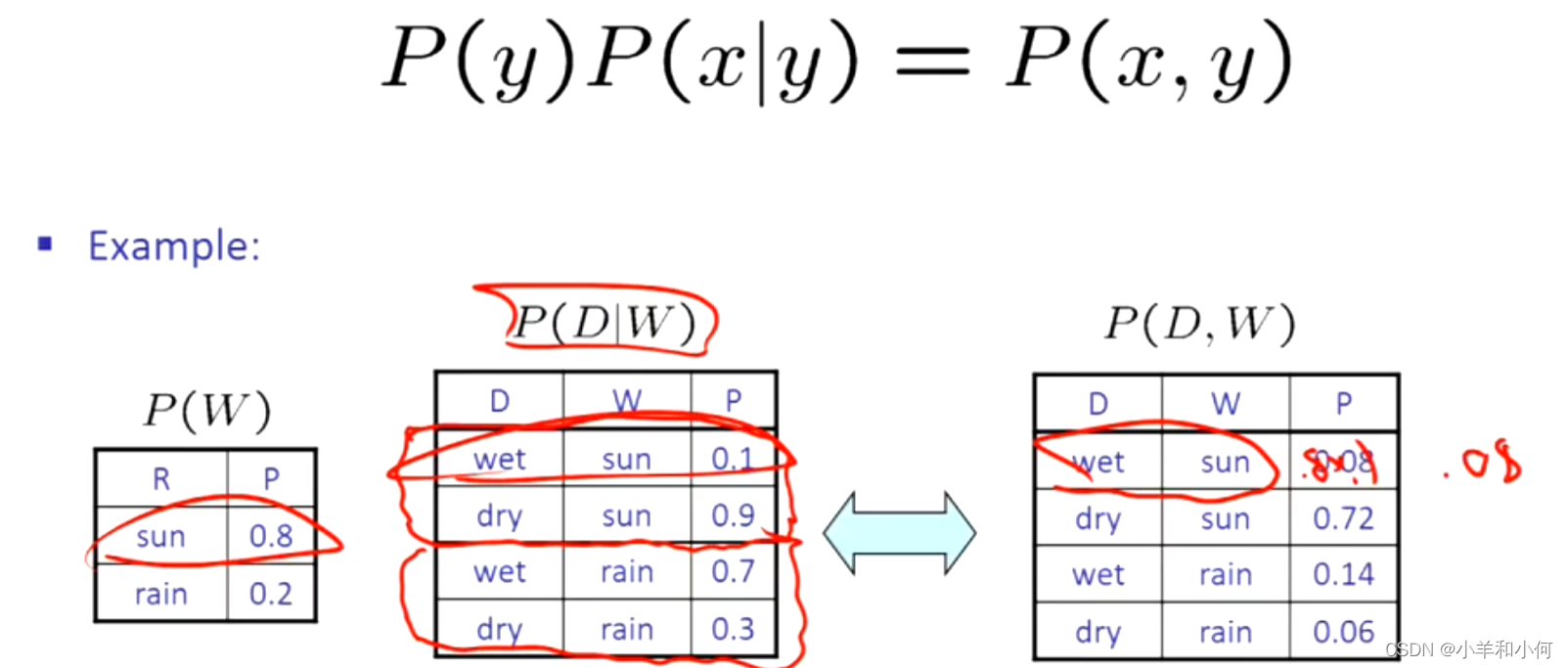
一般来说,存在链式法则,如果想在任意数量的变量上加入分布,可以像下面这样构建:
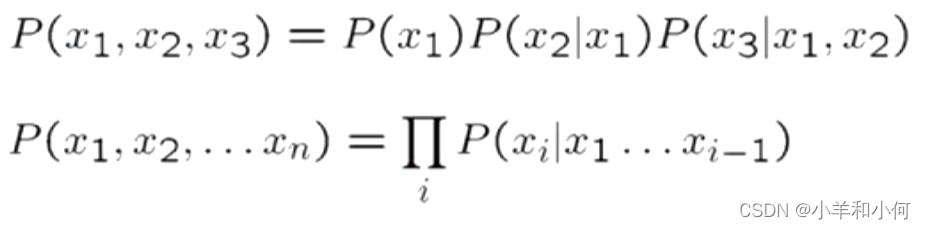
7.3.1 贝叶斯法则
两个变量的联合分布的两种方法:
![]()
![]()
7.4 概率计算公式
条件概率:

枚举推理:

独立性:

贝叶斯法则:
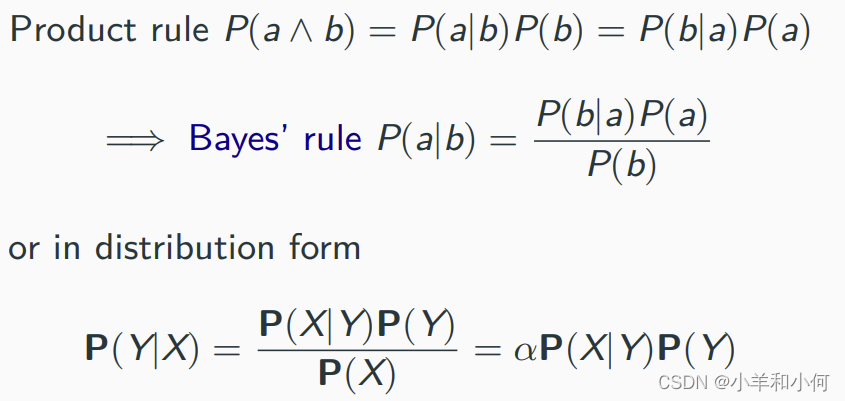
Global semantics:
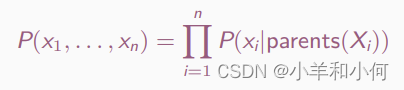
联合查询:
![]()
使用CPT条目的乘积重写完整的联合条目:
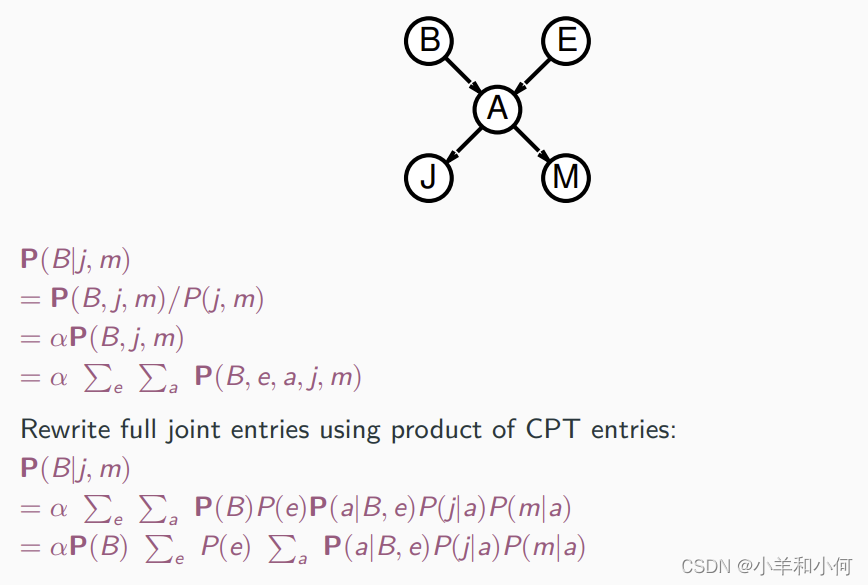
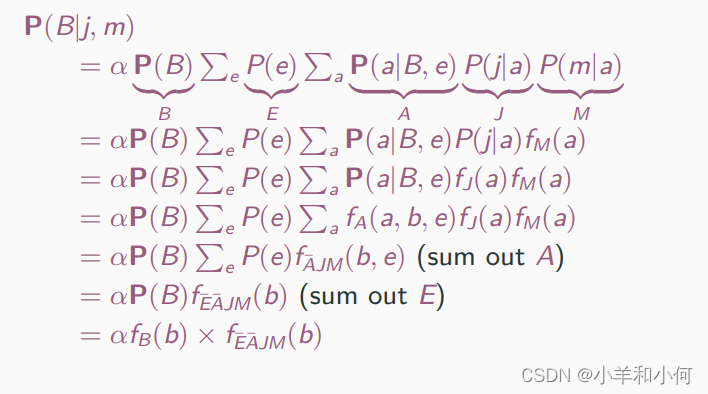
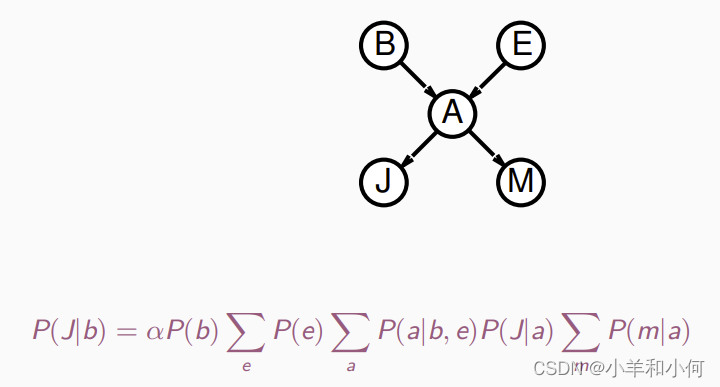
全概率定理:

例如,我们要求的概率,
包括
。
那么根据全概率定理,
Incremental Bayes




