【C语言】-- 数据结构 -- 归并排序类(归并排序)(超详解+动图+源码)_归并排序c语言

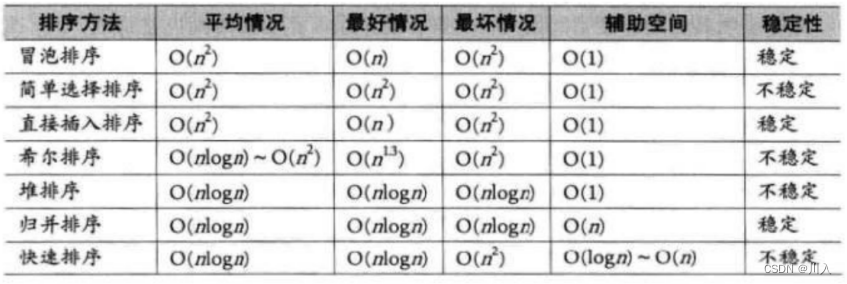
 常见排序：

1. 排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
2. 稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i] = r[j] ，且 r[i] 在 r[j] 之前，而在排序后的序列中，r[i] 仍在 r[j] 之前，则称这种排序算法是稳定的；否则称为不稳定的。
3. 内部排序：数据元素全部放在内存中的排序。
4. 外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

目录

归并排序类：

  1、归并排序：

1.1 书写方式

1.1 递归方式：

1.2 非递归方式：

2. 归并排序的特性总结：

2.1 时间复杂度：

2.2 空间复杂度：

2.3 稳定性：

---

归并排序类：

  1、归并排序：

          归并排序的基本思想： 归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有 序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

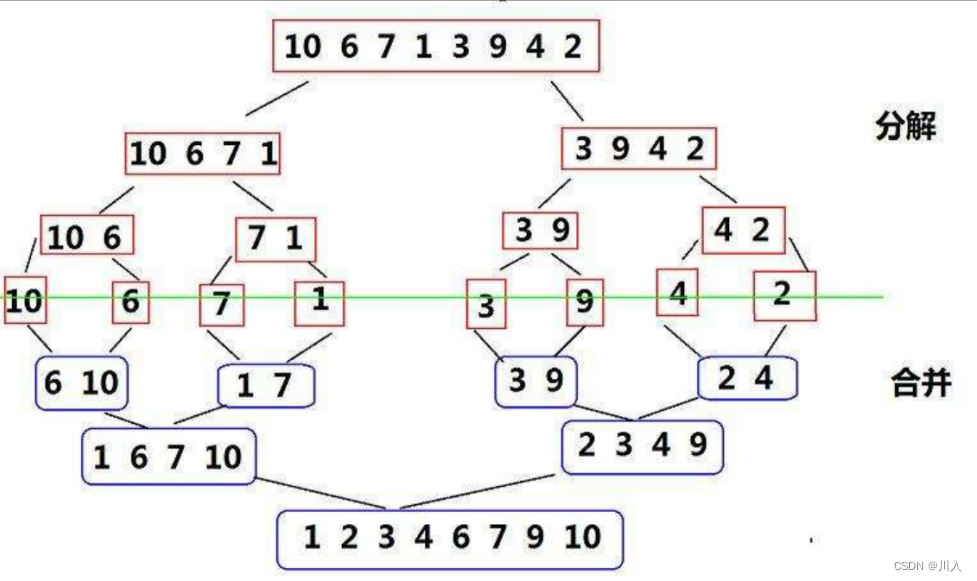
           此为递归实现的方法图 (递归实现易于理解)

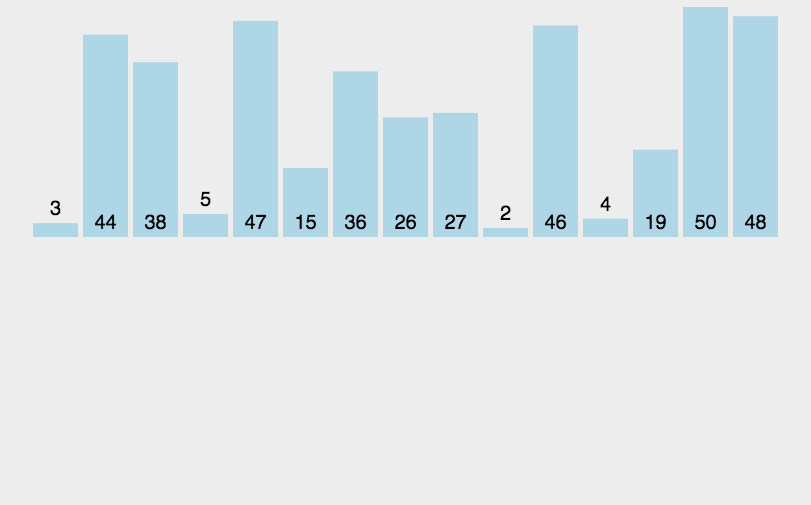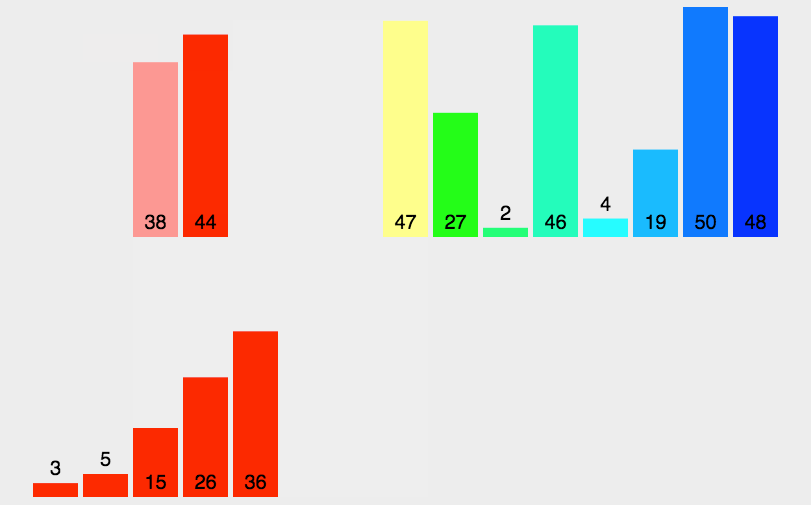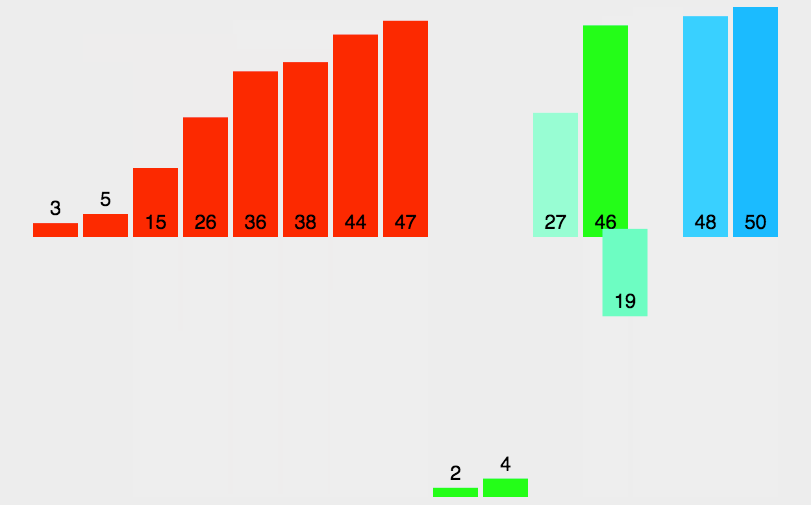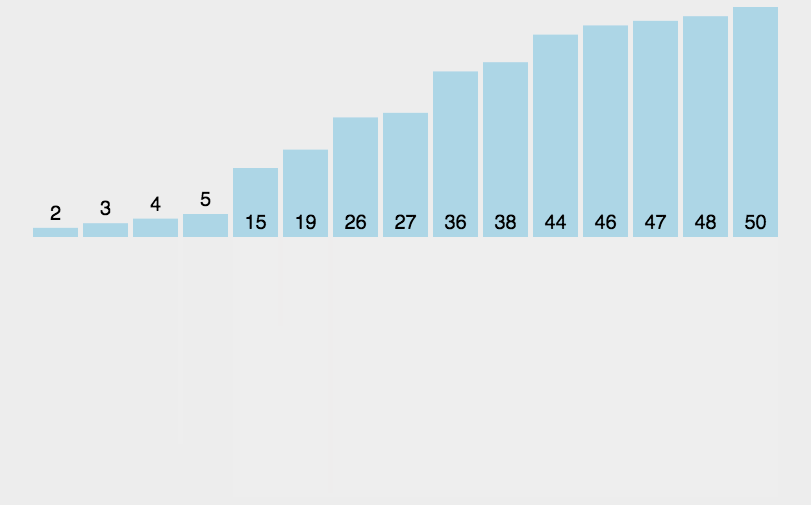
1.1 书写方式

1.1 递归方式：

//归并排序的核心实现
void _MerceSort(int* a, int begin, int end, int* tmp)
{
	assert(a && tmp);
 
	if (begin >= end)
		return;
 
	//利用递归
	int midi = (begin + end) / 2;
 
	_MerceSort(a, begin, midi, tmp);
	_MerceSort(a, midi + 1, end, tmp);
 
	// [begin, mid] [mid+1, end] 分治递归，让子区间有序
	int begin1 = begin, end1 = midi;
	int begin2 = midi + 1, end2 = end;
 
	int j = begin1;
 
	//进行比较排序
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
			tmp[j++] = a[begin1++];
		else
			tmp[j++] = a[begin2++];
	}
 
	//防止未排序完毕
	while (begin1 <= end1)
	{
		tmp[j++] = a[begin1++];
	}
 
	while (begin2 <= end2)
	{
		tmp[j++] = a[begin2++];
	}
	
	//覆盖拷贝回去
	memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
//归并排序
void MerceSort(int* a, int n)
{
	assert(a);
 
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
 
	_MerceSort(a, 0, n - 1, tmp);
 
	free(tmp);
}

1.2 非递归方式：

//归并排序
void MerceSortRone(int* a, int n)
{
	assert(a);
 
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
 
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
 
 
			// end1越界或者begin2越界，则可以不归并了
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}
			
			int m = end2 - begin1 + 1;
			int j = begin1;
 
			//进行比较排序
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
					tmp[j++] = a[begin1++];
				else
					tmp[j++] = a[begin2++];
			}
 
			//防止未排序完毕
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			//覆盖拷贝回去
			memcpy(a + i, tmp + i, sizeof(int) * m);
		}
		gap *= 2;
	}
	free(tmp);
}

2. 归并排序的特性总结：

• 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
• 时间复杂度：O(N*logN)
• 空间复杂度：O(N)
• 稳定性：稳定

2.1 时间复杂度：

          这也就是归并排序的优势，他有着与最优快速排序的同样速度，并且是保持，在个别情况快速排序会达到令人堪忧的O(N^2)，但是归并排序不会，永远是O(N*logN)。

          归并排序的实现就是完美的利用二分实现。

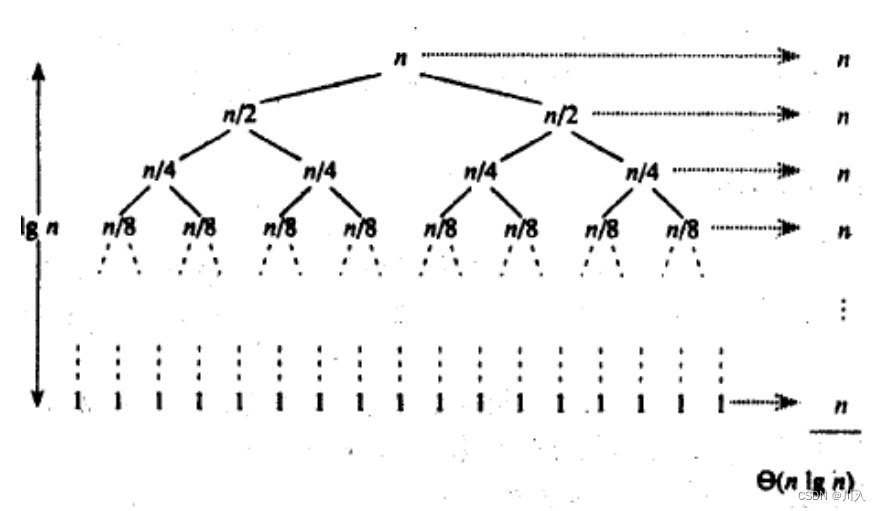
          这种二分实现尤其在递归实现中容易观察出。（递归相当于 1 ~ lgN 层，非递归相当于 lgN ~ 1 层）

2.2 空间复杂度：

          归并排序在时间复杂度的上有着显著的效率，但也代表了它在空间上具有巨大的消耗，在常见的排序中有着稳定的O(n)的空间的巨大消耗。

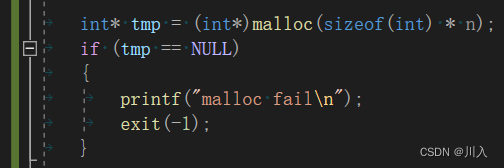
         我们需要开辟一个与代排序序列同样大小的空间。即O(n)。

2.3 稳定性：

         [begin1,end1] 在 [bgein2,end2] 之前，所以在等于的时候 [begin1,end1] 中的必定排前于 [bgein2,end2]。