经验贴：论文中的数学公式都是怎么靠代码实现的?MATLAB运算时间长怎么解决？包含不增序列卷积，复杂公式等_论文中的复杂公式怎么算出来

卷积公式

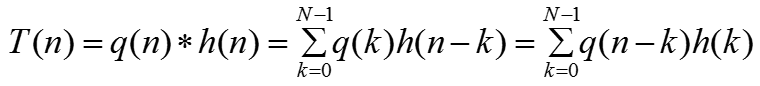
最简单的方法是将其转化到z域，依靠MATLAB工具箱filter，fftfilt函数进行求解 [1]。

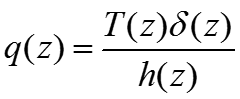
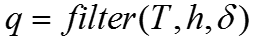
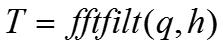
复杂公式

先引入正问题一个半无限大导热分析解（表面温度阶跃+杜哈梅变化）。

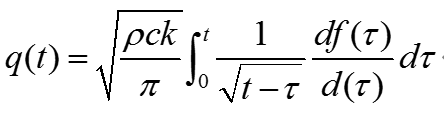
可惜的是时域往往不能求解，需要先用三次样条离散化。

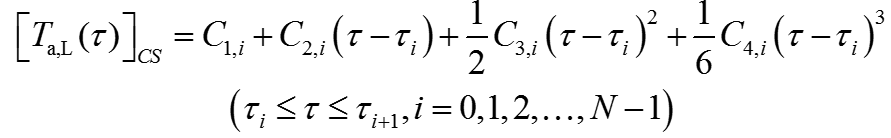
其中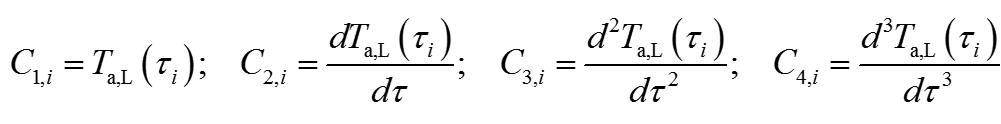
得到离散形式：

其中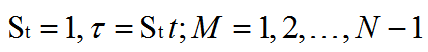

怎么样，这个够复杂了吧，下面贴出代码：

t=csvread('t.csv');
T=csvread('T1.csv');
tt=t(1):0.00001:t(end)
T=interp1(t,T,tt,'spline')
t=tt
pp=csape(t,T)   %默认的边界条件，Lagrange边界条件,求取三次样条结构（断点，系数等） 
format long g
coefs=pp.coefs   %显示每个区间上三次多项式的系数
q=zeros(size(t))
M=1
i=1
Z=0
O=0
C1=5708.74 %常数求取规则不纠结了哈 
for M=1:7000
O=(coefs(M,3)+coefs(M,2)*2*(t(M+1)-t(M))+coefs(M,1)/3*(t(M+1)-t(M))^2)*(t(M+1)-t(M))^0.5-(coefs(M,2)*2+coefs(M,1)*6*(t(M+1)-t(M)))/3*(t(M+1)-t(M))^1.5+coefs(M,1)*6/10*(t(M+1)-t(M))^2.5
for i=1:M-1
Z=Z+(coefs(i,3)+coefs(i,2)*2*(t(M+1)-t(i))+coefs(i,1)*3*(t(M+1)-t(i))^2)*((t(M+1)-t(i))^0.5-(t(M+1)-t(i+1))^0.5)-(coefs(i,2)*2+coefs(i,1)*6*(t(M+1)-t(i)))/3*((t(M+1)-t(i))^1.5-(t(M+1)-t(i+1))^1.5)+coefs(i,1)*6/10*((t(M+1)-t(i))^2.5-(t(M+1)-t(i+1))^2.5)
end
q(M+1)=2*C1*Z+2*C1*O
O=0
Z=0
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

再引入一个反问题，这个主要是求解表面热流或者温度的6 [2]。
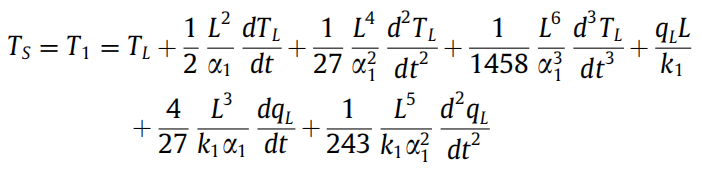
贴代码了哈：

%控制容积法逆问题求热流 
a=1.194E-4  %注意是铜膜 
k=400 %注意是铜膜
C1=zeros(size(t))
C2=zeros(size(t))
E=0.00001  %深度
qs=zeros(size(t))
DTF1=zeros(size(t))
DTF2=zeros(size(t))
DTF3=zeros(size(t))
DTF4=zeros(size(t))
DQF1=zeros(size(t))
DQF2=zeros(size(t))
DQF3=zeros(size(t))

dtf1=(diff(T,1)*10000)   %取701步即0.0001s为步长 
dtf1=dtf1'  %只限于第一次运行，因为df是行需要化成列
for j=1:length(dtf1)
    DTF1(j)=dtf1(j)
end

dtf2=(diff(T,2)*10000)   %取701步即0.0001s为步长 
dtf2=dtf2'  %只限于第一次运行，因为df是行需要化成列
for j=1:length(dtf2)
    DTF2(j)=dtf2(j)
end

dtf3=(diff(T,3)*10000)   %取701步即0.0001s为步长 
dtf3=dtf3'  %只限于第一次运行，因为df是行需要化成列
for j=1:length(dtf3)
    DTF3(j)=dtf3(j)
end

dtf4=(diff(T,4)*10000)   %取701步即0.0001s为步长 
dtf4=dtf4'  %只限于第一次运行，因为df是行需要化成列
for j=1:length(dtf4)
    DTF4(j)=dtf4(j)
end

dqf1=(diff(q,1)*10000)   %取701步即0.0001s为步长 
dqf1=dqf1'  %只限于第一次运行，因为df是行需要化成列
for j=1:length(dqf1)
    DQF1(j)=dqf1(j)
end

dqf2=(diff(q,2)*10000)   %取701步即0.0001s为步长 
dqf2=dqf2'  %只限于第一次运行，因为df是行需要化成列
for j=1:length(dqf2)
    DQF2(j)=dqf2(j)
end

dqf3=(diff(q,3)*10000)   %取701步即0.0001s为步长 
dqf3=dqf3'  %只限于第一次运行，因为df是行需要化成列
for j=1:length(dqf3)
    DQF3(j)=dqf3(j)
end

qs=q+k*((E/a*DTF1)+(19/108*E^3/a^2*DTF2)+(2/243*E^5/a^3*DTF3)+(1/8748*E^7/a^4*DTF4))
   +0.5*E^2/a*DQF1+1/27*E^4/a^2*DQF2+1/1458*E^6/a^3*DQF3
   


%控制容积法逆问题求温度 
a=1.194E-4  %注意是铜膜 
k=400 %注意是铜膜
E=0.00001  %深度
Ts=zeros(size(t))
DTF1=zeros(size(t))
DTF2=zeros(size(t))
DTF3=zeros(size(t))
DQF1=zeros(size(t))
DQF2=zeros(size(t))

dtf1=(diff(T,1)*10000)   %取701步即0.0001s为步长 
dtf1=dtf1'  %只限于第一次运行，因为df是行需要化成列
for j=1:length(dtf1)
    DTF1(j)=dtf1(j)
end

dtf2=(diff(T,2)*10000)   %取701步即0.0001s为步长 
dtf2=dtf2'  %只限于第一次运行，因为df是行需要化成列
for j=1:length(dtf2)
    DTF2(j)=dtf2(j)
end

dtf3=(diff(T,3)*10000)   %取701步即0.0001s为步长 
dtf3=dtf3'  %只限于第一次运行，因为df是行需要化成列
for j=1:length(dtf3)
    DTF3(j)=dtf3(j)
end

dqf1=(diff(q,1)*10000)   %取701步即0.0001s为步长 
dqf1=dqf1'  %只限于第一次运行，因为df是行需要化成列
for j=1:length(dqf1)
    DQF1(j)=dqf1(j)
end

dqf2=(diff(q,2)*10000)   %取701步即0.0001s为步长 
dqf2=dqf2'  %只限于第一次运行，因为df是行需要化成列
for j=1:length(dqf2)
    DQF2(j)=dqf2(j)
end

Ts=T+0.5*E^2/a*DTF1+1/27*E^4/a^2*DTF2+1/1458*E^6/a^3*DTF3+q*E/k
   +4/27*E^3/a/k*DQF1+1/243*E^5/a^2/k*DQF2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106

迭代

迭代真的蛮有意思，其实就是只要我们获取两个关于同一个变量的方程组，就可以把这个变量一直逼近于同时满足这两个方程组的一个值，尽管初值可能离收敛值相差较大。迭代收敛规则一般是迭代次数达到要求或者残差小于预设误差值。

比如如下两个公式：

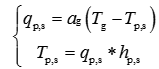
就可以得到变量q的迭代方程组：

for i=1:100 
    q=csvread('q.csv')
	T0=fftfilt(q,DT0i) %上文已经提到，卷积过程
	T0=T0./1000000 %注意卷积过程和实际需要的值带来的倍率 
	q=ag*(Tg-q*h)
	plot(T0)
	max(T0)
end
1
2
3
4
5
6
7
8

MATLAB运算速度慢怎么办

个人体会，请尽可能减少for语句的使用吧！成效不是十倍这么简单！

参考文献

[1]: Taler J. Theory of transient experimental techniques for surface heat transfer[J]. International Journal of Heat and Mass Transfer, 1996, 39(17): 3733-3748.
[2]: Sahoo N, Peetala R K. Transient surface heating rates from a nickel film sensor using inverse analysis[J]. International Journal of Heat and Mass Transfer, 2011, 54(5-6): 1297-1302.