devbox
繁依Fanyi0
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

C++ 实现二叉搜索树_c++二叉检索树

作者：繁依Fanyi0 | 2024-03-16 00:52:06

赞

踩

c++二叉检索树

一.二叉搜索树的基本概念

    二叉搜索树，也叫二叉排序树，是一种具有特殊性质的二叉树。

  • 若左子树不空，则左子树上所有节点的值都小于根节点的值。

  • 若右子树不空，则右子树上所有节点的值都大于根节点的值。

  • 任意节点的子树也都是二叉搜索树。

如下面这颗二叉树：

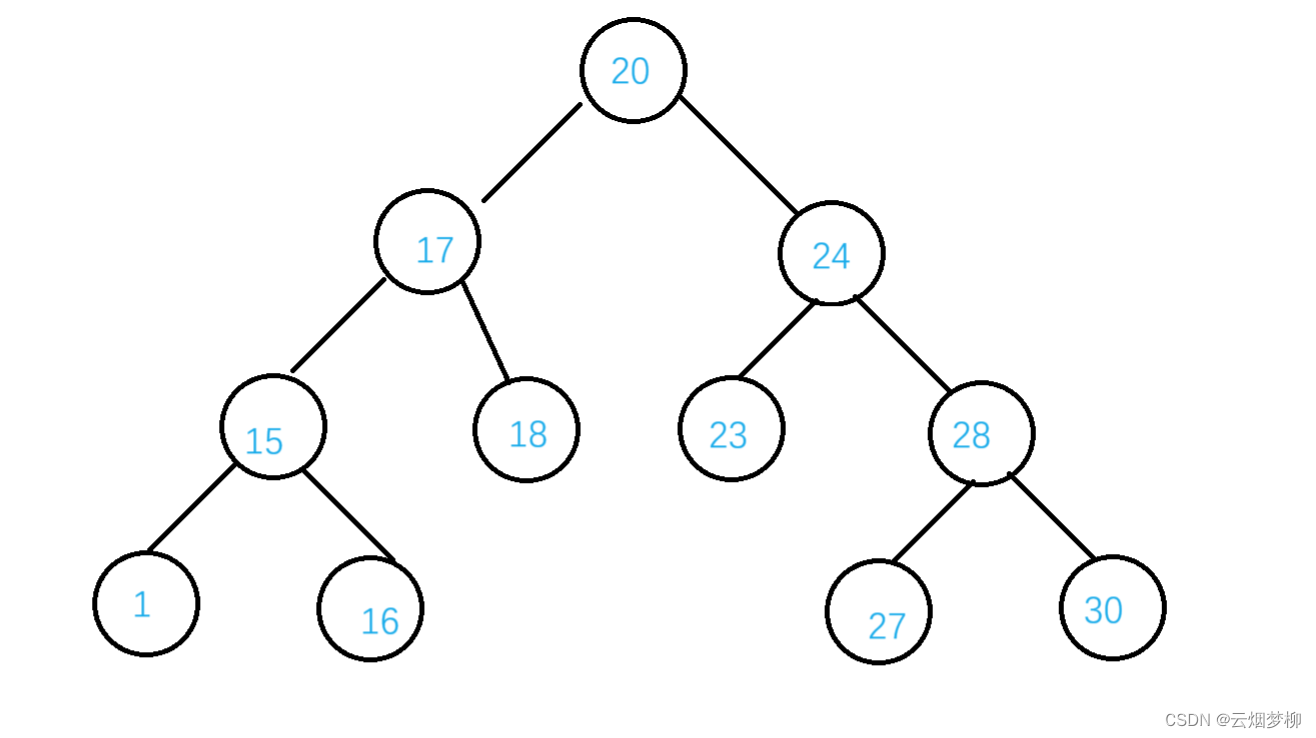 我们可以看出这个二叉树符合上面的规则。

并且二叉搜索树还有一个重要的特点：

二叉搜索树的中序遍历，如果排序的是数字的话，那么他的中序遍历结果一定是个有序的数组，上面这个树的中序遍历为[1 15 16 17 18 20 23 24 27 28 30].

 二.key模型和key-value模型

概念：

  key的模型是指每个节点只有一个键值，用于确定节点在树中的位置。节点的键值必须满足二叉搜索树的性质，即左子节点的键值小于父节点的键值，右子节点的键值大于父节点的键值。这种模型比较简单，但是不能存储额外的信息。
  key/value模型是指每个节点有一个键值和一个数据值，键值用于确定节点在树中的位置，数据值用于存储节点的附加信息。节点的键值仍然必须满足二叉搜索树的性质，但是数据值可以是任意类型或对象。这种模型比较灵活，可以实现一些高级功能，比如映射或字典。

  一般而言，我们在程序中使用的都是key-value模型的二叉搜索树，因为key模型的没什么实际作用。

   假设你想要存储图书的话，在key/value模型中就可以让图书姓名当作键值，数量当作数据值，以此来详细统计一下图书。

   但是我们先由易到难，先来讲解一下key模型的二叉搜索树。

三.key模型的二叉搜索树操作

  3.1 节点

  无论是哪种模型，我们都需要定义一个内部类来表示节点，根据树的基本含义我们可以得知，除了key模型所需要的一个元素之外，我们还需要左右两个指针来表示每个节点的左孩子右孩子。

  故得出：

  1. 	template<typename  K>
  2. 	class BSTreeNode  //二叉搜索树的节点类
  3. 	{
  4. 	public:
  5. 		BSTreeNode(const K& key = K())
  6. 			:_left(nullptr)
  7. 			,_right(nullptr)
  8. 			,_key(key)
  9. 		{}
  10. 		BSTreeNode<K>* _left;
  11. 		BSTreeNode<K>* _right;
  12. 		K _key;
  13. 	};

  3.2 二叉树的表示

 在整个二叉树的类中，我们只要保证有一个头节点就好了，因为他会指向自己的左右孩子。

故得出：

  1. template<class K>
  2. class BSTree
  3. {
  4. 	typedef BSTreeNode<K> Node; //typedef一下节省代码量
  5. private：
  6. 	Node* _root = nullptr;
  7. };

3.3 二叉搜索树的插入

3.3.1 思想

  二叉搜索树的插入其实只需要注意一点，那就是，插入后，仍然保持二叉搜索树的性质。

  那么我们就要与原有的树上的值进行比较，到了合适的位置后再进行插入。 

  比如说这张图：

如果我们要插入的值为 19 的话，需要进行如下几段比较

因此，平衡二叉树的插入实际上就是一个 比较大小 直到寻找到空位置 再进行插入的过程 。

但是，如果插入的元素在数中已经有了该怎么办呢？

平衡二叉树的key模型基本上是拒绝重复元素的插入的。（难办就别办了）

3.3.2 代码实现 

  1. bool Insert(const K& key)
  2. 		{
  3. 			//特殊情况，如果头节点为nullptr，直接插入
  4. 			if (_root == nullptr) 
  5. 			{
  6. 				_root = new Node(key);
  7. 				return true;
  8. 			}
  9.  
  10. 			//记录父节点，以方便链接 
  11. 			Node* parent = nullptr;
  12. 			//真正的遍历比较节点
  13. 			Node* cur = _root;
  14. 			//进行比较
  15. 			while (cur)
  16. 			{
  17. 				if (cur->_key < key)
  18. 				{
  19. 					parent = cur;
  20. 					cur = cur->_right;
  21. 				}
  22. 				else if (cur->_key > key)
  23. 				{
  24. 					parent = cur;
  25. 					cur = cur->_left;
  26. 				}
  27. 				else
  28. 				{
  29. 					//待插入的数在树中已经存在，直接不办了
  30. 					return false;
  31. 				}
  32. 			}
  33.  
  34. 			//进行链接
  35. 			cur = new Node(key);
  36. 			//再次进行比较 判断插入的节点是在左边还是右边
  37. 			if (parent->_key < key)
  38. 			{
  39. 				parent->_right = cur;
  40. 			}
  41. 			else
  42. 			{
  43. 				parent->_left = cur;
  44. 			}
  45. 			return true;
  46.  
  47. 		}

3.4 二叉搜索树的查找

3.4.1 简介

  可以说，二叉搜索树在查找上面的进步是很大，他的平均查找速度为O(logN),最坏查找情况为O(N）。（N为树的高度）

  为什么呢，其实类似于二分查找，它每次在查找的时候都只会前往左右区间，也就是直接剔除一半的值，最后便得出平均查找速度。

  最坏查找是因为有特殊情况，（一般是有序）使二叉树退化成单子树，从而大幅降低了查找效率。

如：

 3.4.2 思想

 其实查找也是个比较大小的思想，通过一次一次的比较大小，最终得出结果。

如：

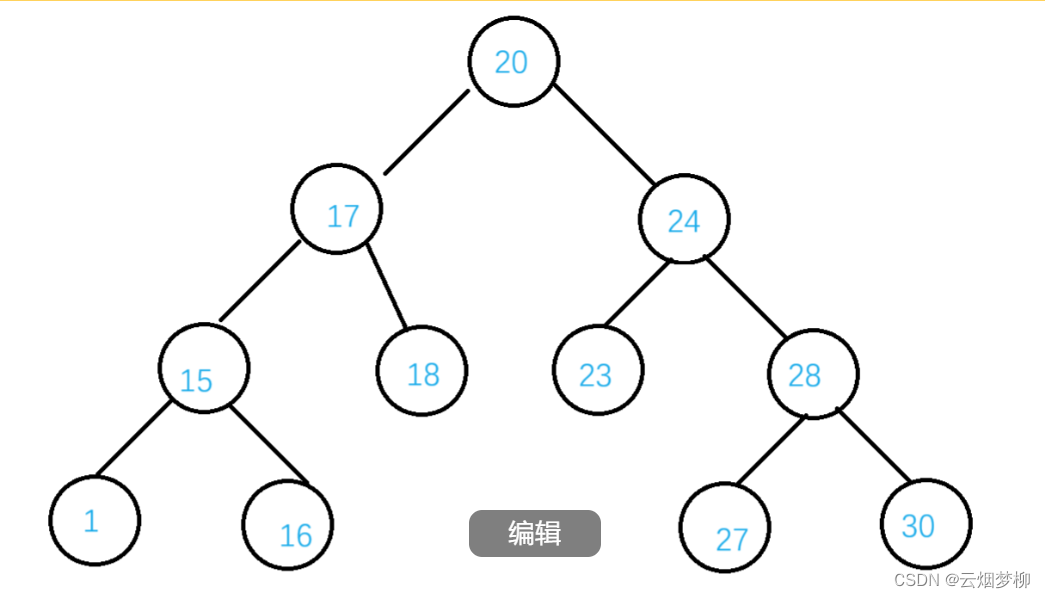
我们要查找  18 

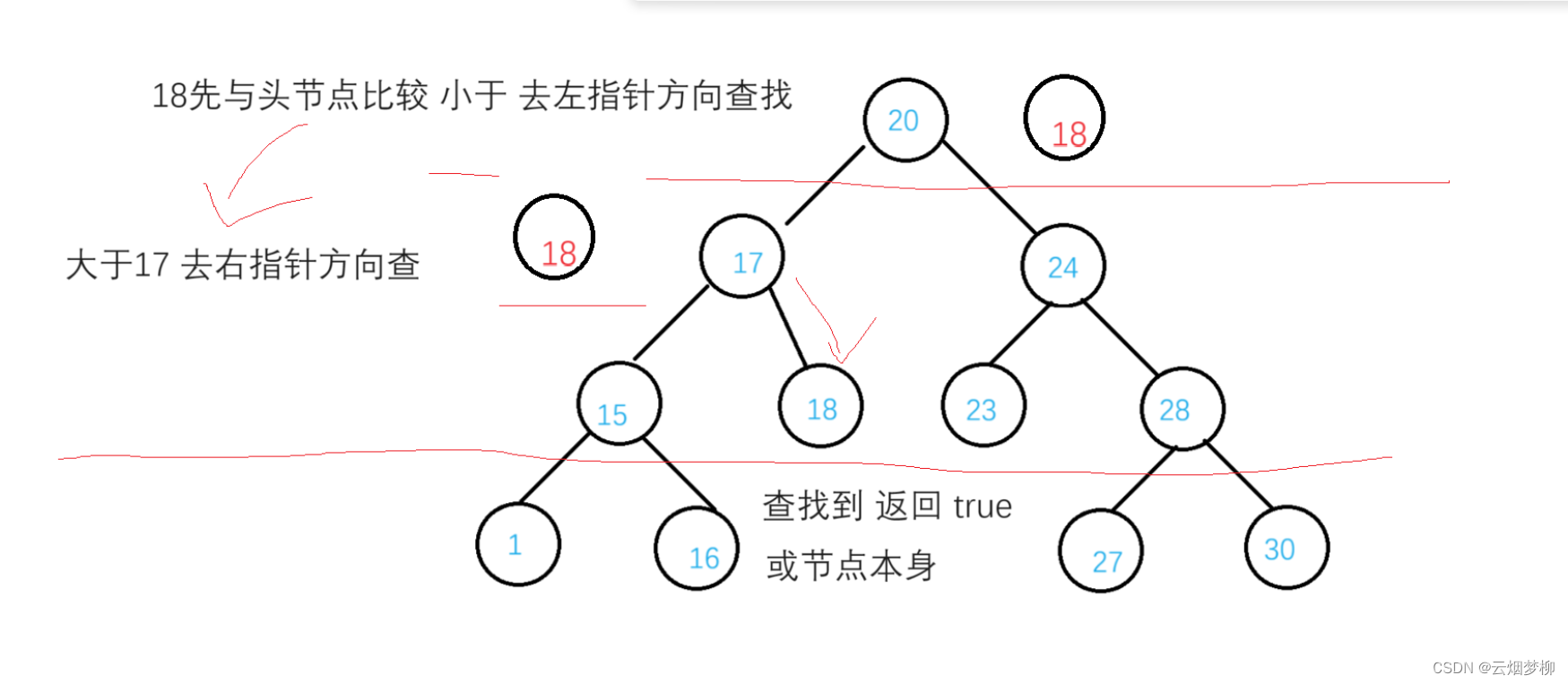
 3.4.3 代码实现

  1. 	Node* Find(const K& key) //我们选择返回节点指针
  2. 		{
  3. 			//通过父子指针进行查找与大小比较
  4. 			Node* parent = nullptr;
  5. 			Node* cur = _root;
  6. 			//进行大小比较
  7. 			while (cur)
  8. 			{
  9. 				if (cur->_key < key)
  10. 				{
  11. 					parent = cur;
  12. 					cur = cur->_right;
  13. 				}
  14. 				else if (cur->_key > key)
  15. 				{
  16. 					parent = cur;
  17. 					cur = cur->_left;
  18. 				}
  19. 				else
  20. 				{
  21. 					//与插入不同，查找到返回节点
  22. 					return cur;
  23. 				}
  24. 			}
  25. 			//没有查找到 返回空
  26. 			return nullptr;
  27. 		}

3.5 二叉搜索树的删除

3.5.1 思想

二叉搜索树的删除和插入一样，都需要保持一个原则，插入后，仍然保持二叉搜索树的性质。

 二叉搜索树的删除无非就四种情况：

1.删除没有孩子节点的父节点

2.删除没有左孩子，但有右孩子的父节点。

3.删除没有有孩子，但有左孩子的节父点。

4.删除有两个孩子的父节点

还是经典老图，稍微改一下，我们分别要删除16 15 28 24这四个节点，分别对应四种情况，我们来看一下。

 

 

 

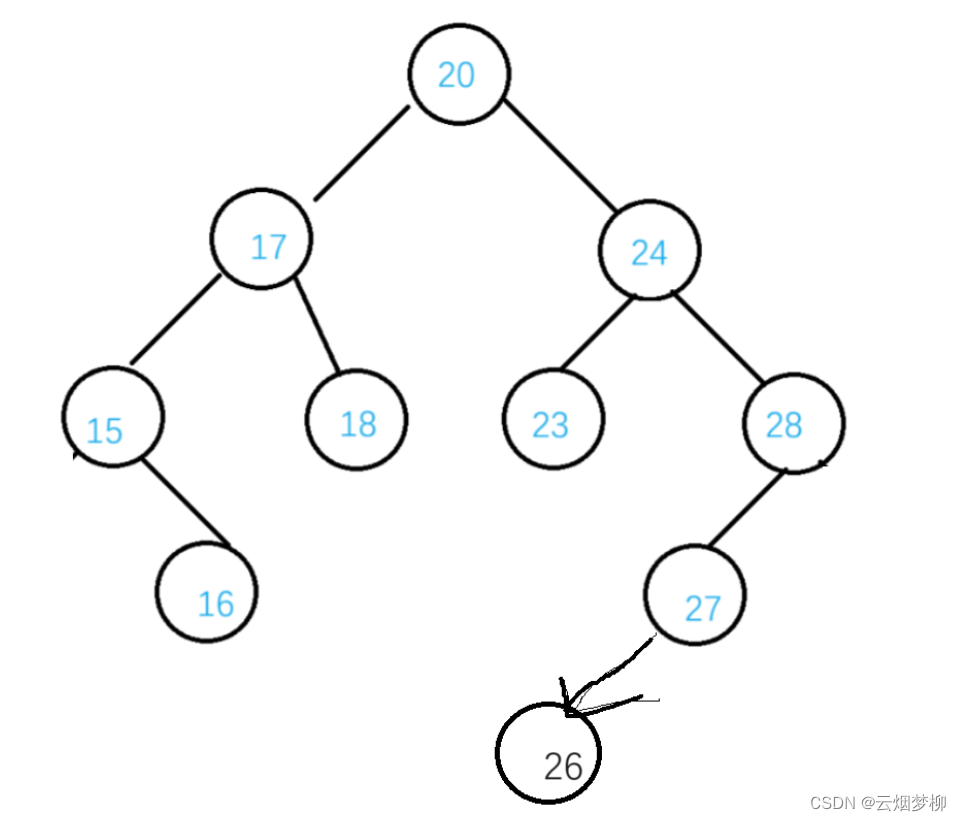
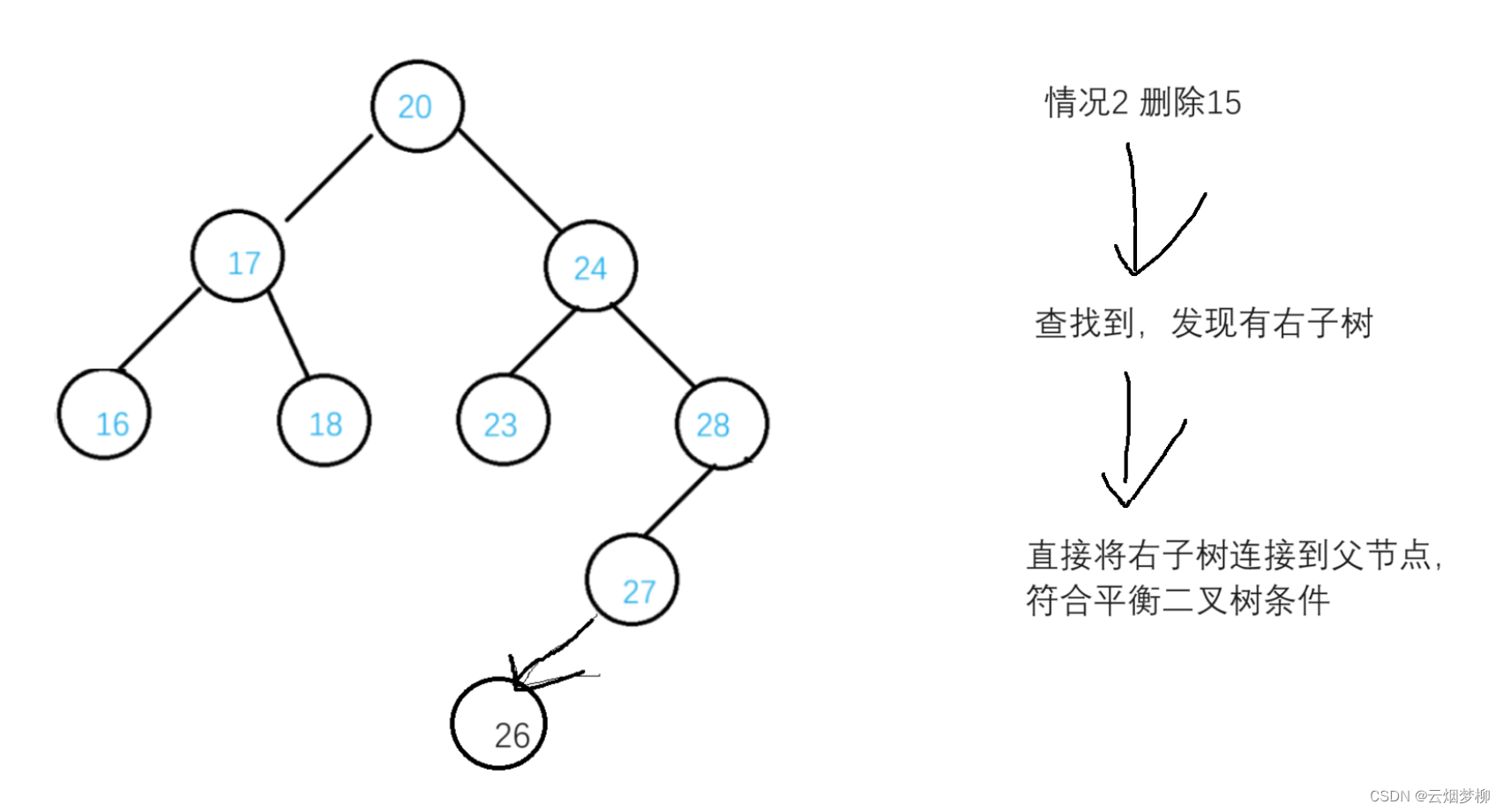
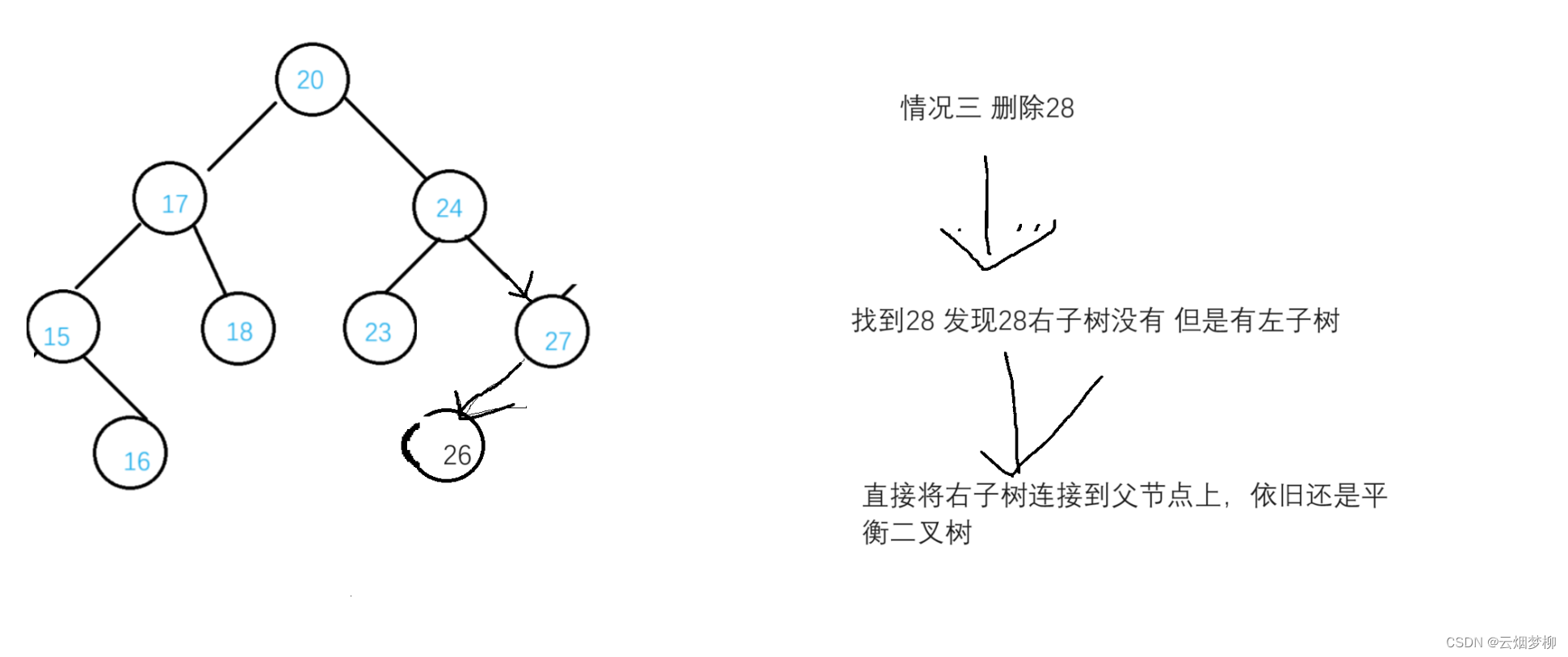
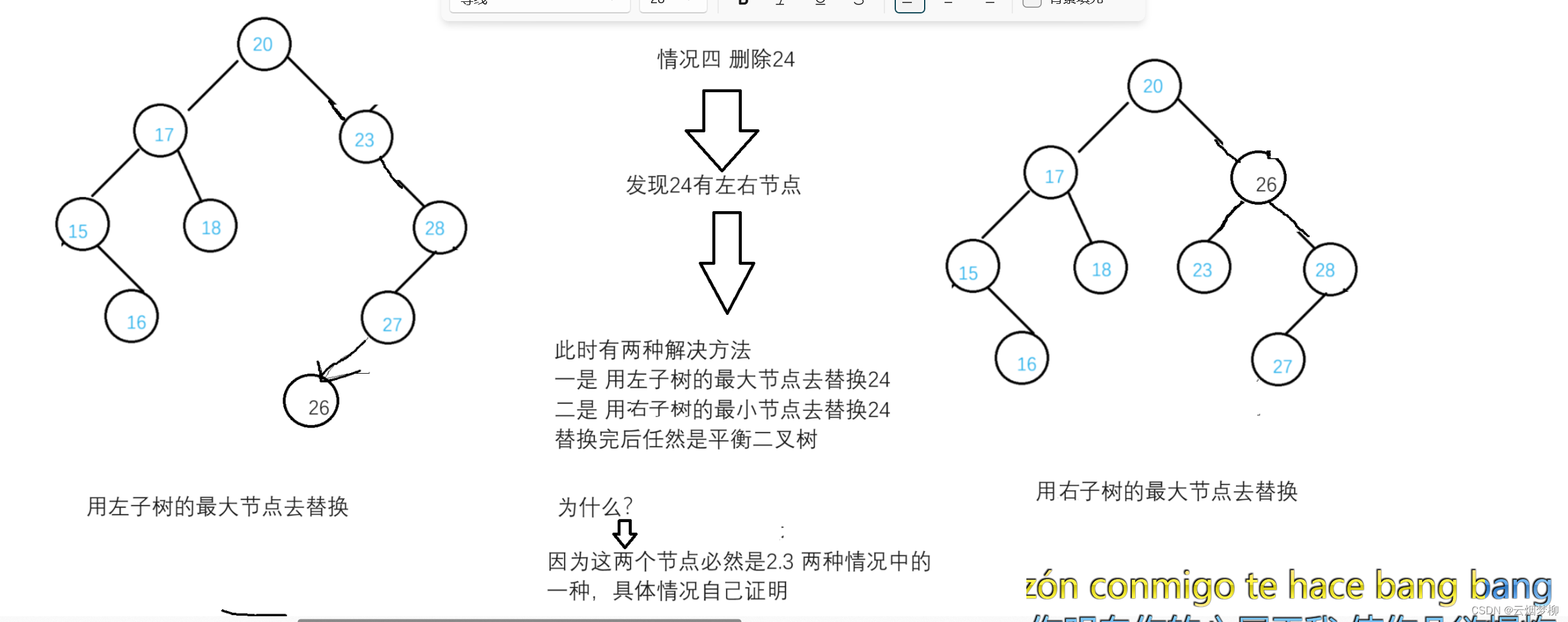
其实第一种情况可以归类为2.3种情况 

 3.5.2 代码实现

  1. 	bool Erase(const K& key)
  2. 		{
  3.  
  4. 			//父指针记录 cur指针查找
  5. 			Node* parent = nullptr;
  6. 			Node* cur = _root;
  7. 			//while循环遍历查找
  8. 			while (cur)
  9. 			{
  10. 				if (cur->_key < key)
  11. 				{
  12. 					parent = cur;
  13. 					cur = cur->_right;
  14. 				}
  15. 				else if (cur->_key > key)
  16. 				{
  17. 					parent = cur;
  18. 					cur = cur->_left;
  19. 				}
  20. 				else
  21. 				{
  22. 					//查找到
  23. 					//开始删除
  24. 					//一共有三种情况
  25.  
  26. 					//待删除节点左指针为nullptr
  27. 					if (cur->_left == nullptr)  //第一二种 情况合起来
  28. 					{ 
  29. 						//处理特殊情况 如果要删除的是头指针
  30. 						if (_root == cur)
  31. 						{
  32. 							_root = cur->_right;
  33. 						}
  34. 						else
  35. 						{
  36. 							//如果是节点左右都为nullptr 父节点的指针就指向nullptr
  37. 							if (parent->_left == cur)
  38. 							{
  39. 								parent->_left = cur->_right;
  40. 							}
  41. 							else
  42. 							{
  43. 								parent->_left = cur->_right;
  44. 							}
  45. 						}
  46. 						delete cur;
  47. 						cur = nullptr;
  48. 					}
  49. 					//待删除节点右指针为nullptr
  50. 					else if (cur->_right == nullptr)
  51. 					{
  52. 						//处理特殊情况 如果要删除的是头指针
  53. 						if (_root == cur)
  54. 						{
  55. 							_root = cur->_left;
  56. 						}
  57. 						else
  58. 						{
  59. 							if (parent->_right == cur)
  60. 							{
  61. 								parent->_right = cur->_left;
  62. 							}
  63. 							else
  64. 							{
  65. 								parent->_right = cur->_left;
  66. 							}
  67. 						}
  68. 						delete cur;
  69. 						cur = nullptr;
  70. 					}
  71.  
  72. 					//待删除节点左右孩子都有
  73. 					else
  74. 					{
  75. 						//查找左子树的最大值 其实就是查找cur左子树的最右节点
  76. 						/*Node* maxParent = cur;
  77. 						Node* max = cur->_left;
  78. 						while (max->_right)
  79. 						{
  81. 							maxParent = max;
  82. 							max =max->_left;
  83. 						}*/
  84.  
  85. 						Node* minParent = cur;
  86. 						Node* min = cur->_right;
  87. 						//查找右子树的最小值 其实就是查找cur右子树的最左节点
  88. 						while (min->_left)
  89. 						{
  90.  
  91. 							minParent = min;
  92. 							min = min->_left;
  93. 						}
  94. 						//将找到的值和cur交换
  95. 						swap(cur->_key, min->_key);
  96.  
  97. 						//如果查找到的最大值或者最小值 还有另外的节点 需要链接
  98. 						if (minParent->_left == min)
  99. 							minParent->_left = min->_right;
  100. 						else
  101. 							minParent->_right = min->_right;
  102.  
  103.  
  104. 						delete min;
  105. 						min = nullptr;
  106. 					}
  107. 					return true;
  108. 				}
  109. 			}
  110. 			//没有删除返回false
  111. 			return false;
  112. 		}

3.6 中序遍历

没啥可说的 普通二叉树的遍历罢了，除了中序遍历可能是一个有序数组外这一个性质外。

  1. void _InOrder(Node* root)
  2. {
  3. 			if (root == nullptr)
  4. 			{
  5. 				return;
  6. 			}
  7. 			_InOrder(root->_left);
  8. 			cout << root->_key << endl;
  9. 			_InOrder(root->_right);
  10.  
  11. }

3.7 总代码

  1. template<typename  K>
  2. 	class BSTreeNode  //二叉搜索树的节点类
  3. 	{
  4. 	public:
  5. 		BSTreeNode(const K& key = K())
  6. 			:_left(nullptr)
  7. 			,_right(nullptr)
  8. 			,_key(key)
  9. 		{}
  10. 		BSTreeNode<K>* _left;
  11. 		BSTreeNode<K>* _right;
  12. 		K _key;
  13. 	};
  14. 	template<class K>
  15. 	class BSTree
  16. 	{
  17. 		typedef BSTreeNode<K> Node; //typedef一下节省代码量
  18. 	public:
  19. 		bool Insert(const K& key)
  20. 		{
  21. 			//特殊情况，如果头节点为nullptr，直接插入
  22. 			if (_root == nullptr) 
  23. 			{
  24. 				_root = new Node(key);
  25. 				return true;
  26. 			}
  27.  
  28. 			//记录父节点，以方便链接 
  29. 			Node* parent = nullptr;
  30. 			//真正的遍历比较节点
  31. 			Node* cur = _root;
  32. 			//进行比较
  33. 			while (cur)
  34. 			{
  35. 				if (cur->_key < key)
  36. 				{
  37. 					parent = cur;
  38. 					cur = cur->_right;
  39. 				}
  40. 				else if (cur->_key > key)
  41. 				{
  42. 					parent = cur;
  43. 					cur = cur->_left;
  44. 				}
  45. 				else
  46. 				{
  47. 					//待插入的数在树中已经存在，直接不办了
  48. 					return false;
  49. 				}
  50. 			}
  51.  
  52. 			//进行链接
  53. 			cur = new Node(key);
  54. 			//再次进行比较 判断插入的节点是在左边还是右边
  55. 			if (parent->_key < key)
  56. 			{
  57. 				parent->_right = cur;
  58. 			}
  59. 			else
  60. 			{
  61. 				parent->_left = cur;
  62. 			}
  63. 			return true;
  64.  
  65. 		}
  66. 		Node* Find(const K& key) //我们选择返回节点指针
  67. 		{
  68. 			//通过父子指针进行查找与大小比较
  69. 			Node* parent = nullptr;
  70. 			Node* cur = _root;
  71. 			//进行大小比较
  72. 			while (cur)
  73. 			{
  74. 				if (cur->_key < key)
  75. 				{
  76. 					parent = cur;
  77. 					cur = cur->_right;
  78. 				}
  79. 				else if (cur->_key > key)
  80. 				{
  81. 					parent = cur;
  82. 					cur = cur->_left;
  83. 				}
  84. 				else
  85. 				{
  86. 					//与插入不同，查找到返回节点
  87. 					return cur;
  88. 				}
  89. 			}
  90. 			//没有查找到 返回空
  91. 			return nullptr;
  92. 		}
  93. 		bool Erase(const K& key)
  94. 		{
  95.  
  96. 			//父指针记录 cur指针查找
  97. 			Node* parent = nullptr;
  98. 			Node* cur = _root;
  99. 			//while循环遍历查找
  100. 			while (cur)
  101. 			{
  102. 				if (cur->_key < key)
  103. 				{
  104. 					parent = cur;
  105. 					cur = cur->_right;
  106. 				}
  107. 				else if (cur->_key > key)
  108. 				{
  109. 					parent = cur;
  110. 					cur = cur->_left;
  111. 				}
  112. 				else
  113. 				{
  114. 					//查找到
  115. 					//开始删除
  116. 					//一共有三种情况
  117.  
  118. 					//待删除节点左指针为nullptr
  119. 					if (cur->_left == nullptr)  //第一二种 情况合起来
  120. 					{ 
  121. 						//处理特殊情况 如果要删除的是头指针
  122. 						if (_root == cur)
  123. 						{
  124. 							_root = cur->_right;
  125. 						}
  126. 						else
  127. 						{
  128. 							//如果是节点左右都为nullptr 父节点的指针就指向nullptr
  129. 							if (parent->_left == cur)
  130. 							{
  131. 								parent->_left = cur->_right;
  132. 							}
  133. 							else
  134. 							{
  135. 								parent->_left = cur->_right;
  136. 							}
  137. 						}
  138. 						delete cur;
  139. 						cur = nullptr;
  140. 					}
  141. 					//待删除节点右指针为nullptr
  142. 					else if (cur->_right == nullptr)
  143. 					{
  144. 						//处理特殊情况 如果要删除的是头指针
  145. 						if (_root == cur)
  146. 						{
  147. 							_root = cur->_left;
  148. 						}
  149. 						else
  150. 						{
  151. 							if (parent->_right == cur)
  152. 							{
  153. 								parent->_right = cur->_left;
  154. 							}
  155. 							else
  156. 							{
  157. 								parent->_right = cur->_left;
  158. 							}
  159. 						}
  160. 						delete cur;
  161. 						cur = nullptr;
  162. 					}
  163.  
  164. 					//待删除节点左右孩子都有
  165. 					else
  166. 					{
  167. 						//查找左子树的最大值 其实就是查找cur左子树的最右节点
  168. 						/*Node* maxParent = cur;
  169. 						Node* max = cur->_left;
  170. 						while (max->_right)
  171. 						{
  173. 							maxParent = max;
  174. 							max =max->_left;
  175. 						}*/
  176.  
  177. 						Node* minParent = cur;
  178. 						Node* min = cur->_right;
  179. 						//查找右子树的最小值 其实就是查找cur右子树的最左节点
  180. 						while (min->_left)
  181. 						{
  182.  
  183. 							minParent = min;
  184. 							min = min->_left;
  185. 						}
  186. 						//将找到的值和cur交换
  187. 						swap(cur->_key, min->_key);
  188.  
  189. 						//如果查找到的最大值或者最小值 还有另外的节点 需要链接
  190. 						if (minParent->_left == min)
  191. 							minParent->_left = min->_right;
  192. 						else
  193. 							minParent->_right = min->_right;
  194.  
  195.  
  196. 						delete min;
  197. 						min = nullptr;
  198. 					}
  199. 					return true;
  200. 				}
  201. 			}
  202. 			//没有删除返回false
  203. 			return false;
  204. 		}
  205.  
  206. 		void InOrder()
  207. 		{
  208. 			_InOrder(_root);
  209. 			cout << endl;
  210. 		}//为了预防数据被改，我们改成privat
  211. 	private:
  212. 		void _InOrder(Node* root)
  213. 		{
  214. 			if (root == nullptr)
  215. 			{
  216. 				return;
  217. 			}
  218. 			_InOrder(root->_left);
  219. 			cout << root->_key << endl;
  220. 			_InOrder(root->_right);
  221.  
  222. 		}
  223. 		Node* _root = nullptr;
  224. 	};

四 .Key-Value模型的搜索二叉树

  如果说key模型的值只能表示在不在的话，那么key-value模型就可以表示通过一个值查找另一个值。

  key value模型 与上述实现的二叉搜索树实现功能差不多，只是增加了一个模板参数value。

代码为：

  1. template<class K, class V>
  2. class BSTreeNode
  3. {
  4. public:
  5. 	BSTreeNode(const K& key=K(),const V& val=V())
  6. 		:_left(nullptr)
  7. 		,_right(nullptr)
  8. 		,_key(key)
  9. 		,_val(val)
  10. 	{
  11. 	}
  12. 	BSTreeNode<K, V>* _left;
  13. 	BSTreeNode<K, V>* _right;
  14. 	K _key;
  15. 	V _val;
  16. };
  17. template<class K, class V>
  18. class BSTree
  19. {
  20. 	typedef BSTreeNode<K, V> Node; //这里我们重命名一下，节省代码
  21. public:
  22. 	bool Insert(const K& key, const V& value)
  23. 	{
  24. 		if (_root == nullptr)
  25. 		{
  26. 			_root = new Node(key, value);
  27. 			return true;
  28. 		}
  29.  
  30. 		Node* parent = nullptr;
  31. 		Node* cur = _root;
  32. 		while (cur)
  33. 		{
  34. 			if (cur->_key < key)
  35. 			{
  36. 				parent = cur;
  37. 				cur = cur->_right;
  38. 			}
  39. 			else if (cur->_key > key)
  40. 			{
  41. 				parent = cur;
  42. 				cur = cur->_left;
  43. 			}
  44. 			else
  45. 			{
  46. 				return false;
  47. 			}
  48. 		}
  49.  
  50. 		cur = new Node(key, value);
  51. 		if (parent->_key < key)
  52. 		{
  53. 			parent->_right = cur;
  54. 		}
  55. 		else
  56. 		{
  57. 			parent->_left = cur;
  58. 		}
  59. 		return true;
  60.  
  61. 	}
  62. 	Node* Find(const K& key)
  63. 	{
  64. 		Node* parent = nullptr;
  65. 		Node* cur = _root;
  66. 		while (cur)
  67. 		{
  68. 			if (cur->_key < key)
  69. 			{
  70. 				parent = cur;
  71. 				cur = cur->_right;
  72. 			}
  73. 			else if (cur->_key > key)
  74. 			{
  75. 				parent = cur;
  76. 				cur = cur->_left;
  77. 			}
  78. 			else
  79. 			{
  80. 				return cur;
  81. 			}
  82. 		}
  83. 		return nullptr;
  84. 	}
  85. 	bool Erase(const K& key)
  86. 	{
  87. 		Node* parent = nullptr;
  88. 		Node* cur = _root;
  89. 		while (cur)
  90. 		{
  91. 			if (cur->_key < key)
  92. 			{
  93. 				parent = cur;
  94. 				cur = cur->_right;
  95. 			}
  96. 			else if (cur->_key > key)
  97. 			{
  98. 				parent = cur;
  99. 				cur = cur->_left;
  100. 			}
  101. 			else
  102. 			{
  103. 				//开始删除
  104. 				//一共有三种情况
  105. 				if (cur->_left == nullptr)
  106. 				{
  107. 					if (_root == cur)
  108. 					{
  109. 						_root = cur->_right;
  110. 					}
  111. 					else
  112. 					{
  113. 						if (parent->_left == cur)
  114. 						{
  115. 							parent->_left = cur->_right;
  116. 						}
  117. 						else
  118. 						{
  119. 							parent->_left = cur->_right;
  120. 						}
  121. 					}
  122. 					delete cur;
  123. 					cur = nullptr;
  124. 				}
  125. 				else if (cur->_right == nullptr)
  126. 				{
  127. 					if (_root == cur)
  128. 					{
  129. 						_root = cur->_left;
  130. 					}
  131. 					else
  132. 					{
  133. 						if (parent->_right == cur)
  134. 						{
  135. 							parent->_right = cur->_left;
  136. 						}
  137. 						else
  138. 						{
  139. 							parent->_right = cur->_left;
  140. 						}
  141. 					}
  142. 					delete cur;
  143. 					cur = nullptr;
  144. 				}
  145. 				else
  146. 				{
  147.  
  148. 					Node* minParent = cur;
  149. 					Node* min = cur->_right;
  150.  
  151. 					while (min->_left)
  152. 					{
  153. 						
  154. 						minParent = min;
  155. 						min = min->_left;
  156. 					}
  157. 					swap(cur->_key, min->_key);
  158. 	
  159. 					if (minParent->_left == min)
  160. 						minParent->_left = min->_right;
  161. 					else 
  162. 						minParent->_right = min->_right;
  163. 					delete min;
  164. 					min = nullptr;
  165. 				}
  166. 				return true;
  167. 			}
  168. 		}
  169. 		return false;
  170. 	}
  171. 	
  172. 	void InOrder()
  173. 	{
  174. 		_InOrder(_root);
  175. 		cout << endl;
  176. 	}
  177. private:
  178. 	void _InOrder(Node* root)
  179. 	{
  180. 		if (root == nullptr)
  181. 		{
  182. 			return;
  183. 		}
  184. 		_InOrder(root->_left);
  185. 		cout << root->_key << ":" << root->_val<< endl;
  186. 		_InOrder(root->_right);
  187.  
  188. 	}
  189. 	Node* _root = nullptr;
  190. };

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/繁依Fanyi0/article/detail/245838
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号