决策树_二叉搜索的决策树

1. KDTREE

kd树（k-dimensional树的简称），是一种分割k维数据空间的数据结构。主要应用于多维空间关键数据的搜索（如：范围搜索和最近邻搜索）。

上图的树就是一棵KDTree，形似二叉搜索树，其实KDTree就是二叉搜索树的变种。这里的K = 3.

首先来看下树的组织原则。将每一个元组按0排序（第一项序号为0，第二项序号为1，第三项序号为2），在树的第n层，第 n%3 项被用粗体显示，而这些被粗体显示的树就是作为二叉搜索树的key值，比如，根节点的左子树中的每一个节点的第一个项均小于根节点的的第一项，右子树的节点中第一项均大于根节点的第一项，子树依次类推。

对于这样的一棵树，对其进行搜索节点会非常容易，给定一个元组，首先和根节点比较第一项，小于往左，大于往右，第二层比较第二项，依次类推。

1.1 从二叉搜索树谈起

先看一个标准的BSTree，每个节点只有一个key值。

将key值对应到一维的坐标轴上。

根节点对应的就是2，左子树都在2的左边，右子树都在2的右边，整个一维空间就被根节点分割成了两个部分，当要查找结点0的时候，由于是在2的左边，所以可以放心的只搜索左子树的部分。整个搜索的过程可以看成不断分割搜索区间的过程，直到找到目标节点。这样的分割可以扩展到二维甚至更多维的情况。在BSTree中，节点分割的是一维数轴，那么在二维中，就应当是分割平面了，就像这样：

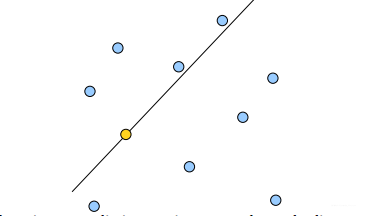
黄色的点作为根节点，上面的点归左子树，下面的点归右子树，接下来再不断地划分，最后得到一棵树就是赫赫有名的BSPTree（binary space partitioning tree）. 分割的那条线叫做分割超平面（splitting hyperplane），在一维中是一个点，二维中是线，三维的是面。

KDTree就是超平面都垂直于轴的BSPTree。同样的数据集，用KDTree划分之后就是这样：

黄色节点就是Root节点，下一层是红色，再下一层是绿色，再下一层是蓝色。为了更好的理解KDTree的分割，我们在图形中来形象地看一下搜索的过程，假设现在需要搜寻右下角的一个点，首先要做的就是比较这个点的x坐标和root点的x坐标值，由于x坐标值大于root节点的x坐标，所以只需要在右边搜寻，接下来，要比较该节点和右边红色节点y值得大小…后面依此类推。
下面要说的就是关于KDTree的两个最重要的问题：
1.树的建立；
2.最近邻域搜索（Nearest-Neighbor Lookup）。

1.2 树的建立

先定义一下节点的数据结构。每个节点应当有下面几个域：
Node-data - 数据矢量， 数据集中某个数据点，是n维矢量（这里也就是k维）
Range - 空间矢量， 该节点所代表的空间范围
split - 整数， 垂直于分割超平面的方向轴序号
Left - k-d树， 由位于该节点分割超平面左子空间内所有数据点所构成的k-d树
Right - k-d树， 由位于该节点分割超平面右子空间内所有数据点所构成的k-d树
parent - k-d树， 父节点
建立树最大的问题在于轴点（pivot）的选择，选择好轴点之后，树的建立就和BSTree差不多了。
建树必须遵循两个准则：
1.建立的树应当尽量平衡，树越平衡代表着分割得越平均，搜索的时间也就是越少。
2.最大化邻域搜索的剪枝机会。

第一种选取轴点的策略是median of the most spread dimension pivoting strategy，对于所有描述子数据（特征矢量），统计他们在每个维度上的数据方差，挑选出方差中最大值，对应的维就是split域的值。数据方差大说明沿该坐标轴方向上数据点分散的比较开。这个方向上，进行数据分割可以获得最好的平衡。数据点集Data-Set按照第split维的值排序，位于正中间的那个数据点 被选为轴点。

1.3 最近邻搜索

给定一个KDTree和一个节点，求KDTree中离这个节点最近的节点.(这个节点就是最临近点)。这里距离的求法用的是欧式距离。

基本的思路很简单：首先通过二叉树搜索（比较待查询节点和分裂节点的分裂维的值，小于等于就进入左子树分支，等于就进入右子树分支直到叶子结点），顺着“搜索路径”很快能找到最近邻的近似点，也就是与待查询点处于同一个子空间的叶子结点；然后再回溯搜索路径，并判断搜索路径上的结点的其他子结点空间中是否可能有距离查询点更近的数据点，如果有可能，则需要跳到其他子结点空间中去搜索（将其他子结点加入到搜索路径）。重复这个过程直到搜索路径为空。

这里还有几个细节需要注意一下，如下图，假设标记为星星的点是 test point， 绿色的点是找到的近似点，在回溯过程中，需要用到一个队列，存储需要回溯的点，在判断其他子节点空间中是否有可能有距离查询点更近的数据点时，做法是以查询点为圆心，以当前的最近距离为半径画圆，这个圆称为候选超球（candidate hypersphere），如果圆与回溯点的轴相交，则需要将轴另一边的节点都放到回溯队列里面来。

判断轴是否与候选超球相交的方法可以参考下图：

下面再用一个例子来具体说一下查询的过程。假设我们的k-d tree就是上面通过样本集{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}创建的。
我们来查找点(2.1,3.1)，在(7,2)点测试到达(5,4)，在(5,4)点测试到达(2,3)，然后search_path中的结点为<(7,2), (5,4), (2,3)>，从search_path中取出(2,3)作为当前最佳结点nearest, dist为0.141；
然后回溯至(5,4)，以(2.1,3.1)为圆心，以dist=0.141为半径画一个圆，并不和超平面y=4相交，如下图，所以不必跳到结点(5,4)的右子空间去搜索，因为右子空间中不可能有更近样本点了。
于是在回溯至(7,2)，同理，以(2.1,3.1)为圆心，以dist=0.141为半径画一个圆并不和超平面x=7相交，所以也不用跳到结点(7,2)的右子空间去搜索。
至此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2.1,3.1)的最近邻点，最近距离为0.141。

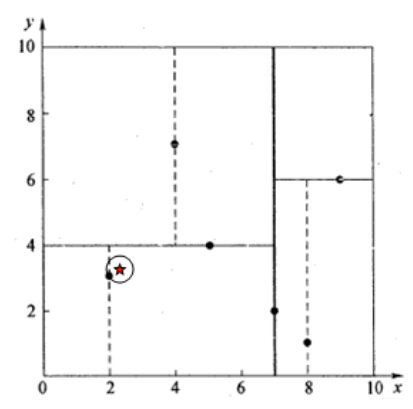
再举一个稍微复杂的例子，我们来查找点(2,4.5)，在(7,2)处测试到达(5,4)，在(5,4)处测试到达(4,7)，然后search_path中的结点为<(7,2), (5,4), (4,7)>，从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202；
然后回溯至(5,4)，以(2,4.5)为圆心，以dist=3.202为半径画一个圆与超平面y=4相交，如下图，所以需要跳到(5,4)的左子空间去搜索。所以要将(2,3)加入到search_path中，现在search_path中的结点为<(7,2), (2, 3)>；另外，(5,4)与(2,4.5)的距离为3.04 < dist = 3.202，所以将(5,4)赋给nearest，并且dist=3.04。
回溯至(2,3)，(2,3)是叶子节点，直接平判断(2,3)是否离(2,4.5)更近，计算得到距离为1.5，所以nearest更新为(2,3)，dist更新为(1.5)
回溯至(7,2)，同理，以(2,4.5)为圆心，以dist=1.5为半径画一个圆并不和超平面x=7相交, 所以不用跳到结点(7,2)的右子空间去搜索。
至此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2,4.5)的最近邻点，最近距离为1.5

2. 决策树

2.1 熵与条件熵

如果利用一个特征进行分类的结果与随机分类的结果没有很大差别，则称这个特征是没有分类能力的（对象是否喜欢打游戏应该不会成为关键特征吧，也许也会……）。为了解决特征选择问题，找出最优特征，先要介绍一些信息论里面的概念。

熵是表示随机变量不确定性的度量。设X 是一个取有限个值的离散随机变量，其概率分布为

则随机变量的熵定义为

条件熵（conditional entropy）

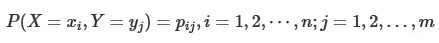
条件熵H(Y|X) 表示在已知随机变量X 的条件下随机变量Y 的不确定性。随机变量X给定的条件下随机变量Y 的条件熵H(Y|X)，定义为X 给定条件下Y 的条件概率分布的熵对X 的数学期望

这里，p_i =P(X=x_i ),i=1,2,⋯,n.

信息增益表示得知特征X 的信息而使得类Y 信息的不确定性减少的程度。特征A 对训练数据集D的信息增益g(D,A) ，定义为集合D的经验熵H(D) 与特征A 给定条件下D 的经验条件熵H(D|A) 之差，即g(D,A)=H(D)−H(D|A)

这个差又称为互信息。信息增益大的特征具有更强的分类能力。
根据信息增益准则的特征选择方法是：对训练数据集（或子集）计算其每个特征的信息增益，选择信息增益最大的特征。

计算信息增益算法的步骤如下：
输入：训练数据集D 和特征A ；
输出：特征A 对训练数据集D 的信息增益g(D,A) .
(1)计算数据集D 的经验熵H(D)

(2)计算特征A 对数据集D 的经验条件熵H(D|A)

(3)计算信息增益
g(D,A)=H(D)−H(D|A)

信息增益比：
特征A A对训练数据集D 的信息增益比g_R (D,A) 定义为其信息增益g(D,A) 与训练数据集D 关于特征A 的值的熵H A (D) 之比，即


n 是特征A 取值的个数。

令L(S) = -P(S) * log2(S)
H(X) =L(X=数学) + L(X=IT) + L(X=英语)
= -0.5 * log2(0.5) - 0.25 * log2(0.25) - 0.25*log2(0.25)
= 0.5 + 0.5 + 0.5 = 1.5

H(Y) = L(Y = M) + L(Y = F)
= -0.5 * log2(0.5) - 0.5 * log2(0.5)
= 0.5 + 0.5 = 1

H(X, Y) = L(X=数学, Y=M) + L(X=IT, Y=M) + L(X=英语, Y=F) + L(X=数学, Y=F)
= -0.25 * log2(0.25) * 4
= 2

以下log表示log2

H(X/Y) = H(X/Y=M)*P(Y=M) + H(X/Y=F)*P(Y=F)即加权平均熵
= [L(X=数学/Y=M)+L(X=数学/Y=M)]*P(Y=M) + H(X/Y=F)*P(Y=F)
= [-0.5 * log(0.5) * 2] * 0.5 + H(X/Y=F)*P(Y=F)
= 0.5 + H(X/Y=F)*P(Y=F)= 0.5 + 0.5 = 1
= H(X, Y) - H(Y)

H(Y/X) = H(Y/X=数学)*P(X=数学)+H(Y/X=IT)*P(X=IT)+H(Y/X=英语)*P(X=英语)
= [-0.5 * log(0.5) * 2] * 0.5+H(Y/X=IT)*P(X=IT)+H(Y/X=英语)*P(X=英语)
= 0.5 + 0 + 0 = 0.5
= H(X, Y) - H(X)

2.2 ID3（只能分类）

ID3算法由Ross Quinlan发明，建立在“奥卡姆剃刀”的基础上：越是小型的决策树越优于大的决策树（be simple简单理论）。ID3算法中根据信息增益评估和选择特征，每次选择信息增益最大的特征作为判断模块建立子结点。ID3算法可用于划分标称型数据集，没有剪枝的过程，为了去除过度数据匹配的问题，可通过裁剪合并相邻的无法产生大量信息增益的叶子节点（例如设置信息增益阀值）。使用信息增益的话其实是有一个缺点，那就是它偏向于具有大量值的属性。就是说在训练集中，某个属性所取的不同值的个数越多，那么越有可能拿它来作为分裂属性，而这样做有时候是没有意义的，另外ID3不能处理连续分布的数据特征，于是就有了C4.5算法。CART算法也支持连续分布的数据特征。

2.3 ID4.5（只能分类）

C4.5算法用信息增益率来选择属性，继承了ID3算法的优点。并在以下几方面对ID3算法进行了改进：
• 克服了用信息增益选择属性时偏向选择取值多的属性的不足；
• 在树构造过程中进行剪枝；
• 能够完成对连续属性的离散化处理；
• 能够对不完整数据进行处理。

ID3和C4.5二者都有贪心性质：即通过局部最优构造全局最优。C4.5算法产生的分类规则易于理解、准确率较高；但效率低，因树构造过程中，需要对数据集进行多次的顺序扫描和排序。也是因为必须多次数据集扫描，C4.5只适合于能够驻留于内存的数据集。对于离散型描述属性，C4.5的处理方法与ID3相同，按照该属性本身的取值个数进行计算；对于某个连续性描述属性Ac，假设在某个结点上的数据集的样本数量为total，该算法采用如下步骤：

• 将该结点上的所有数据样本按照连续型描述属性的具体数值，由小到大进行排序，得到属性值的取值序列{A₁c，A₂c，……A_totalc}。
• 在取值序列中生成total-1个分割点。第i（0<i<total）个分割点的取值设置为V_i=（A_ic+A_i+1c）/2,它可以将该节点上的数据集划分为两个子集。
• 从total-1个分割点中选择最佳分割点。对于每一个分割点划分数据集的方式，计算它的信息增益比，并且从中选择信息增益比最大的分割点来划分数据集。

2.4 CART（能分类，也能回归）

CART，即分类与回归树（classification and regression tree），也是一种应用很广泛的决策树学习方法。但是CART算法比较强大，既可用作分类树，也可以用作回归树。作为分类树时，其本质与ID3、C4.5并有多大区别，只是选择特征的依据不同而已。另外，CART算法建立的决策树一般是二叉树，即特征值只有yes or no的情况。当CART用作回归树时，以最小平方误差作为划分样本的依据。

2.4.1 分类树

基尼指数:
分类树采用基尼指数选择最优特征。假设有K 个类，样本点属于第k 类的概率为p_k ，则概率分布的基尼指数定义为

对于给定的样本集合D ，其基尼指数为

这里，C_k 是D 中属于第k 类的样本子集，K 是类的个数。
那么在给定特征A 的条件下，集合D 的基尼指数定义为

基尼指数Gini(D) 表示集合D的不确定性，基尼指数Gini(D,A) 表示经A=a分割后集合D 的不确定性。基尼指数值越大，样本集合的不确定性也就越大，这一点与熵相似。

做预测的时候，比较测试数据与决策树上的数值，递归执行该过程直到进入叶子结点；最后将测试数据定义为叶子结点所属的类型 。

2.4.1 回归树

回归树的生成实际上也是贪心算法。与分类树不同的是回归树处理的数据连续分布的。对于样本集D，对于属性j，根据其第s 个属性值，将数据集D划分成两部分R1和R2，计算R1中所有样本结果的平均值c1，R2中所有样本结果的平均值c2，然后分别在R1和R2中计算squared error；遍历j的所有属性值，重复上述步骤，选取其中的最小值，作为属性j的最优二分值；对于样本集D，遍历所有属性，重复上述两步，选取其中的最小值，作为最优属性，也即得到了最优（j,s）组合

注意I(x属于Rm)是个视在函数，也就是x属于Rm的时候才取1

2.4 剪枝

生成子树序列{T₀ ,T₁ ,…,T_n }的基本思想是从T₀ 开始，裁剪T_i 中关于训练数据集误差增加最小的分枝来得到T _i+1。实际上，当1棵树T 在节点t 处剪枝时，它的误差增加直观上认为是R(t)−R(T_t )，其中，R(t) 为在节点t 的子树被裁剪后节点t 的误差，R(T_t ) 为在节点t 的子树没被裁剪时子树T t 的误差。然而，剪枝后，T 的叶子数减少了L(T_t )−1 ，其中， L(T_t ) 为子树T_t 的叶子数，也就是说，T 的复杂性减少了。因此，考虑树的复杂性因素，树分枝被裁剪后误差增加率由下式决定：

其中，R(t) 表示节点t 的子树被裁剪后节点t 的误差，R(t)=r(t)∗p(t) ，r(t) 是节点t 的误差率，p(t)是节点t 上的样本个数与训练集中样本个数的比例。R(T_t ) 表示节点t 的子树没被裁剪时子树T_t 的误差，即子树T_t 上所有叶子节点的误差之和。 T_i+1 就是选择T i 中具有最小α 值所对应的剪枝树，这里的i不代表树上的节点，而是迭代号。
顺带补充一下，叶子节点就是没有任何子节点的节点，如下面的t7,t8,t9；子树就是任意选择一个节点作为根节点，其下的所有子子孙孙节点共同组成一颗子树，如子树Tt6就是以t6节点为根节点，t6，t8,t9共同组成的树。

例如：图1中t_i 表示决策树中第i 个节点，A、B表示训练集中的两个类别，A、B之后的数据表示落入该节点分别属于A类、B类的样本个数。

决策树中训练样本总个数为80。对于节点t 4 ，其中，A类样本46个，B类样本4个，根据大多数原则，则节点t 4 中样本为A类，故节点t 4 的子树（t 8 、t 9 ）被裁剪之后t 4 的误差为：(4/50) *(50/80) =4/80 。节点t 4 的子树（t 8 、t 9）被裁剪之前t 4 的误差为：(1/45) *(45/80) +(2/5) *(5/80) =3/80 。故α(t 4 )=(4/80 −3/80)/( 2−1) =0.0125 。类似过程，依次得到所有节点的误差增加率：

在原始树T₀ 行，4个非叶节点中t 4 的α 值最小，因此，裁剪T₀ 的t 4 节点的分枝得到T₁ ；在T 1 行，虽然t 2 和t 3 的α值相同，但裁剪t 2 的分枝可以得到更小的决策树，因此，T 2 是裁剪T 1 中的t 2 分枝得到的。

根据以上产生的子树序列{T₀ ,T₁ ,…,T_n }，最后一颗树Tn就是根节点。再从中选择出1棵最佳决策树，通常采用的方法有两种，一种是V番交叉验证(V-fold cross-validation)，另一种是基于独立剪枝数据集。