计算机图形学笔记十一：Ray Tracing1（阴影，光线追踪基本原理）_光线追踪阴影

1.阴影贴图（Shadow Mapping）

图形学中阴影的产生原理：对于一个点来说，如果它位于阴影中，则说明摄像机能看到这个点，但是光源无法看到这个点；如果位于阴影外，则说明摄像机能看到这个点，同时光源也能看到这个点。
注：

• Shadow Mapping 只能处理点光源的阴影；
• 产生的为硬阴影（没有平滑过渡）；

1.1产生步骤

Step1：从光源出处看向物体，进行一次透视投影，只记录下投影后光能看到的点的深度信息（Z-Buffer）

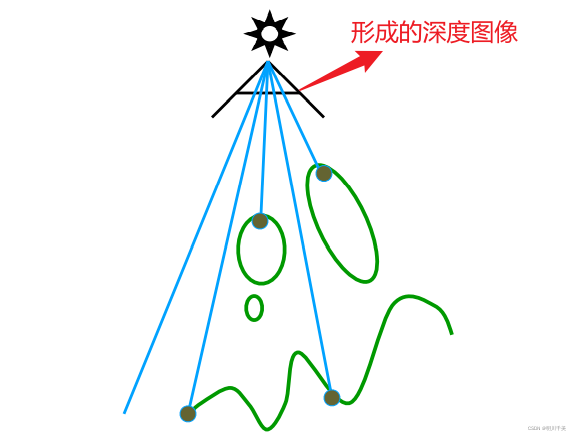
Step2：从真正的相机视角去对当前场景进行透视投影，将相机看到的所有点，全部通重新投影到光源相机上，又会得到一副深度图

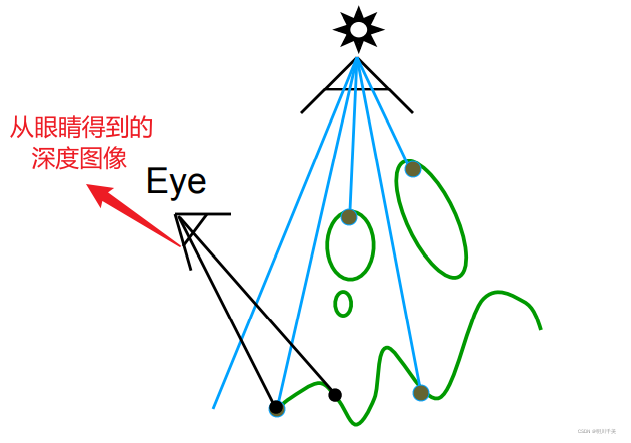
Step3：将Step2中生成的深度图像与Step1中生成的深度图像进行比较，看上面记录的点的深度是否一致（一致则说明点光源能看到该点，即该点不在阴影中，可见；反之在阴影中，不可见）


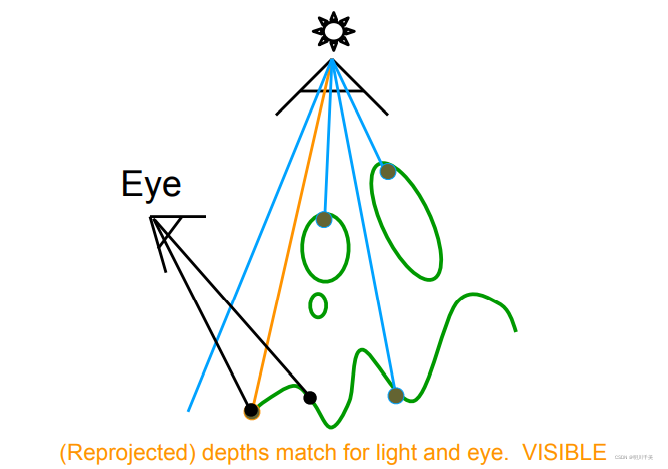
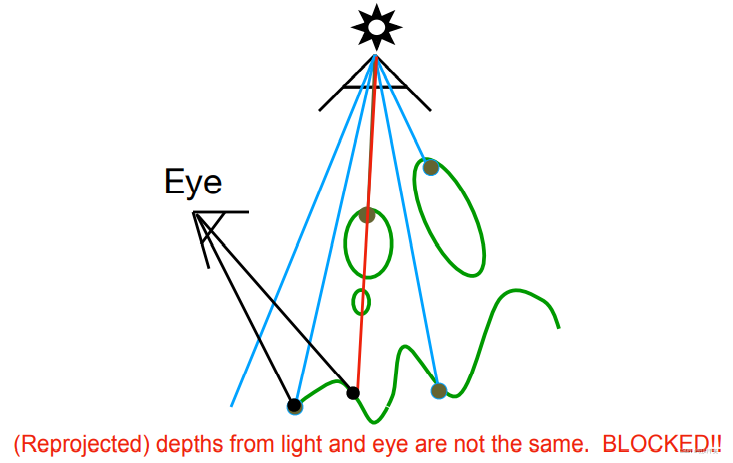
如上图所示，从摄像机投影回光源，进行比较，如橘色线上的点，这点能被光照照射到，就不处于阴影中，可见；而红线上的点就被判定处于阴影中，不可见。

1.2存在问题

1）计算结果均为浮点数，不宜比较是否相等，一般通过让两个浮点数做差，结果小于某个极小的数就认为这两个浮点数相等；
2）由于要求的是点光源，而点光源不存在大小，产生的为硬阴影，不符合实际中的阴影，真实的如下图的第二张图所示，称为软阴影；
3）阴影贴图也是贴图的一种，阴影贴图的分辨率和实际渲染的分辨率如果不匹配，即纹理分辨率过大或过小引起的问题，如锯齿和摩尔纹。

2.光线追踪（ Ray Tracing）

2.1为什么需要光线追踪？

1）光栅化并不能很好的处理全局影响，如下图所示的几种反射：

2）虽然光栅化处理很快，但质量较低，如下图所示：

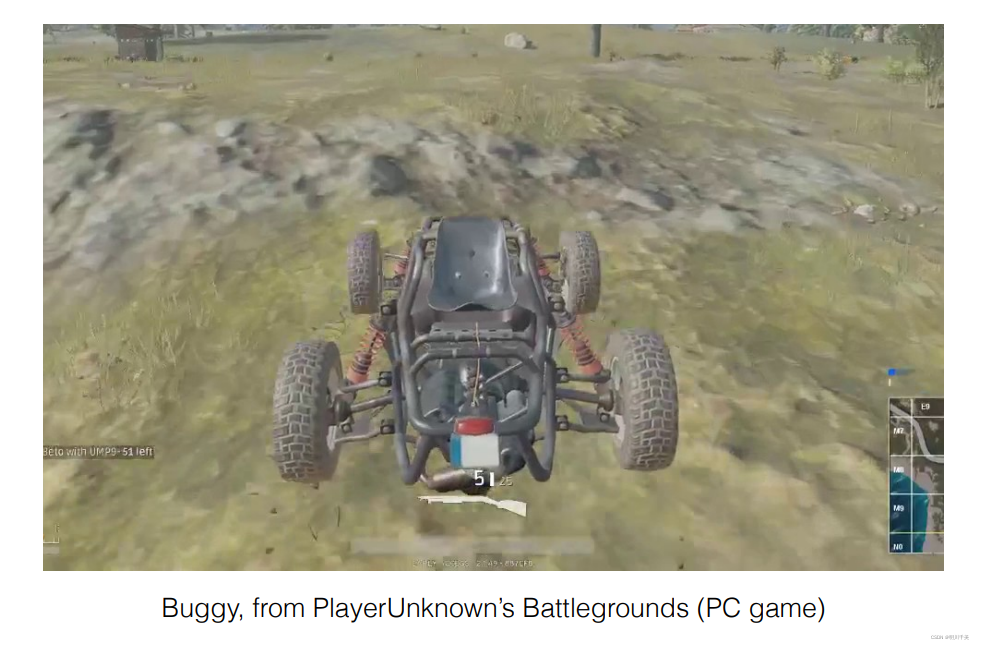
3）由于光线追踪生成速度非常缓慢，一般用于制作动画视频时使用，而光栅化一般使用于实时场景渲染：

2.2基础光线追踪算法（Basic Ray-Tracing Algorithm）

三个思想基础：

• 光总是沿直线传播的
• 光线与光线之间不会发生碰撞
• 光线的可逆性，即光线到达眼睛后，眼睛发出的光同样能返回光源

基础光线追踪的过程：
Step1：从摄像机看向物体，类似发出光线（eye ray），首先穿过图像平面（image plane，透视投影中的近平面），直到最初接触到某个物体的表面；

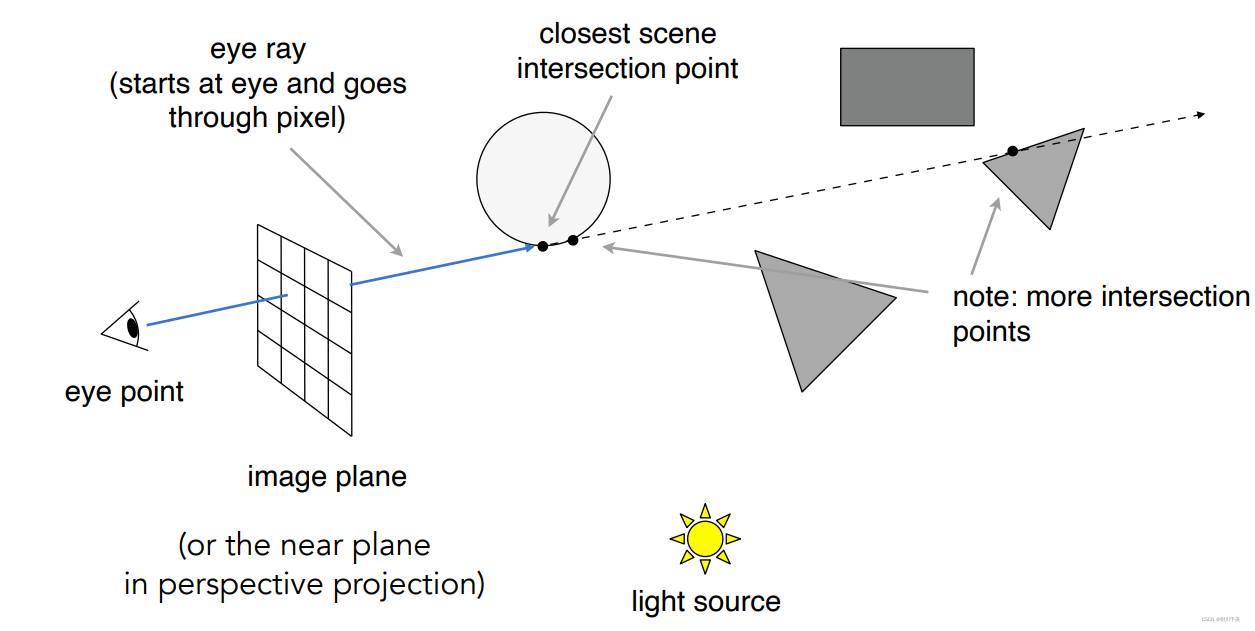
如果一条光线可以穿过多个物体，仍只需记录第一个被照射到的物体，后面的物体默认为被遮挡上了，处于阴影中，眼睛看不到，如上图虚线所示

Step2：将相交点与光源连接，判断是否处于阴影中，若不处于，则在image plane对应的网格位置记录该点的颜色信息等，不断重复操作直到用眼睛发出的光线遍历完image plane中的所有像素点

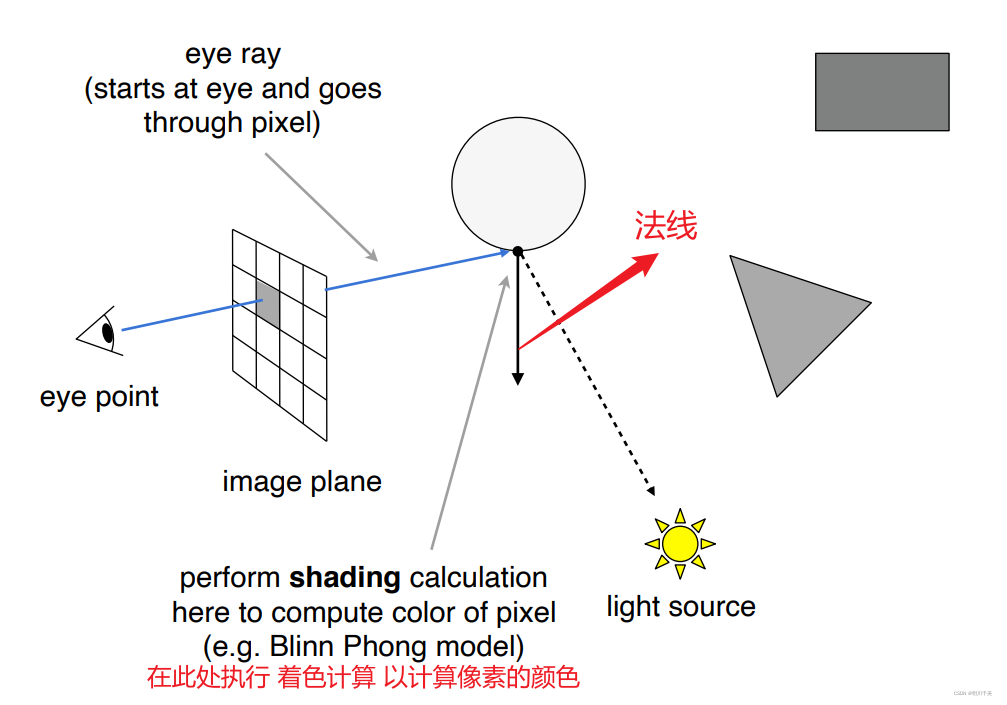
然而，这样做得到的结果与Blinn-Phong光照模型得到的结果一样，缺少现实物体的反射和折射功能，所以引入Whitted风格的光线追踪。

2.3Whitted风格的光线追踪（Whitted-Style Ray Tracing）

Whitted-Style Ray Tracing很不错的解决了折射和反射相关的投影到视觉图上的效果：

实现过程：
Step1：和上述的基础光线追踪的Step1步骤一样，只是有多添加了光线的反射和折射
注：当光线打到光滑的物体表面时，会同时发生折射和反射

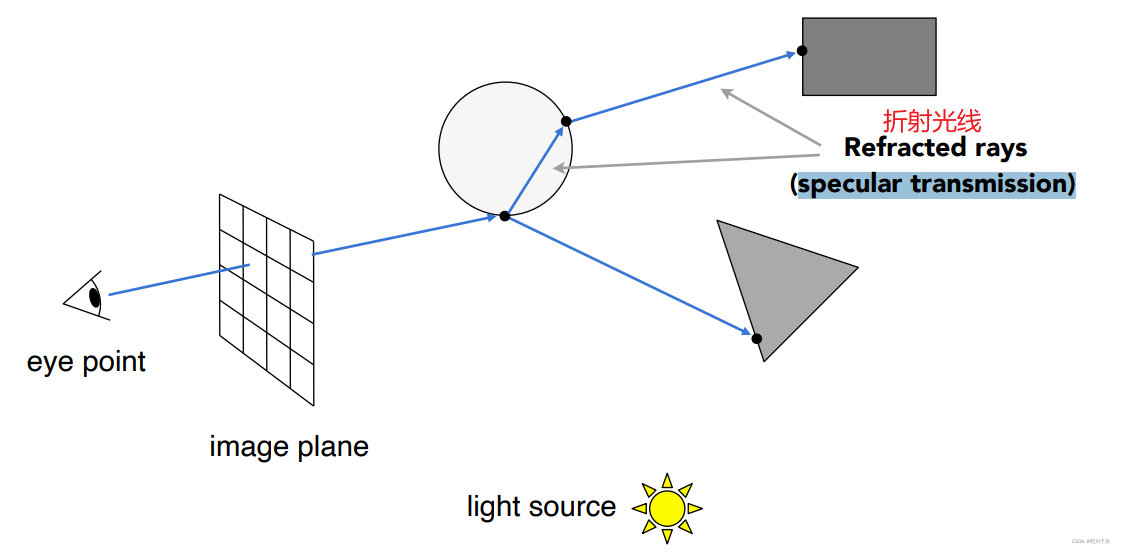
Step2：将上述四个点分别与光源连接，然后在像素块中按一定的权重比例记录下颜色信息（如直射光线60%，折射反射光线占40%等）

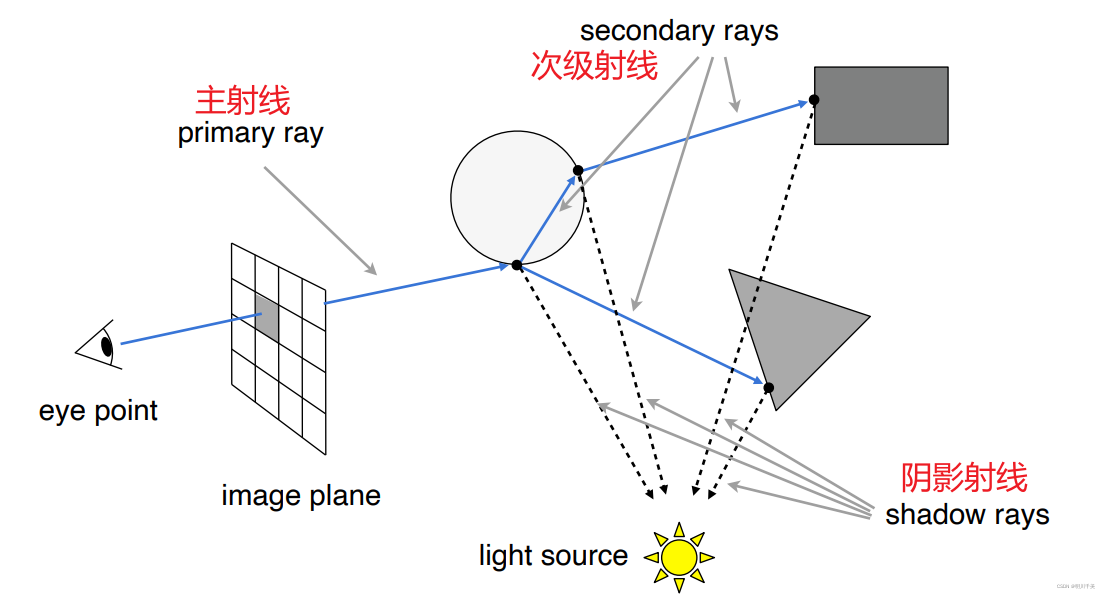
2.4计算光线和物体表面的交点

2.4.1光线的表示

光线就是一条射线，一个向量，由起点，方向和时间构成：

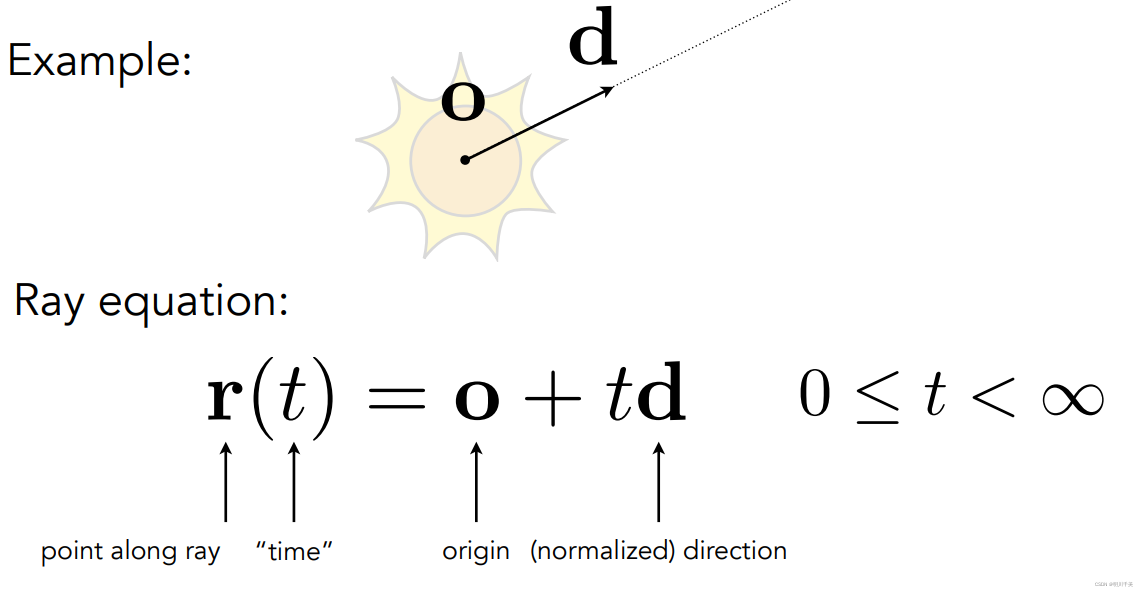
2.4.2光线和隐式曲面的交点

以光线和球的交点为例：
求光线和球的交点实质上就是求同时满足光线方程和球方程的点：

方程求解：

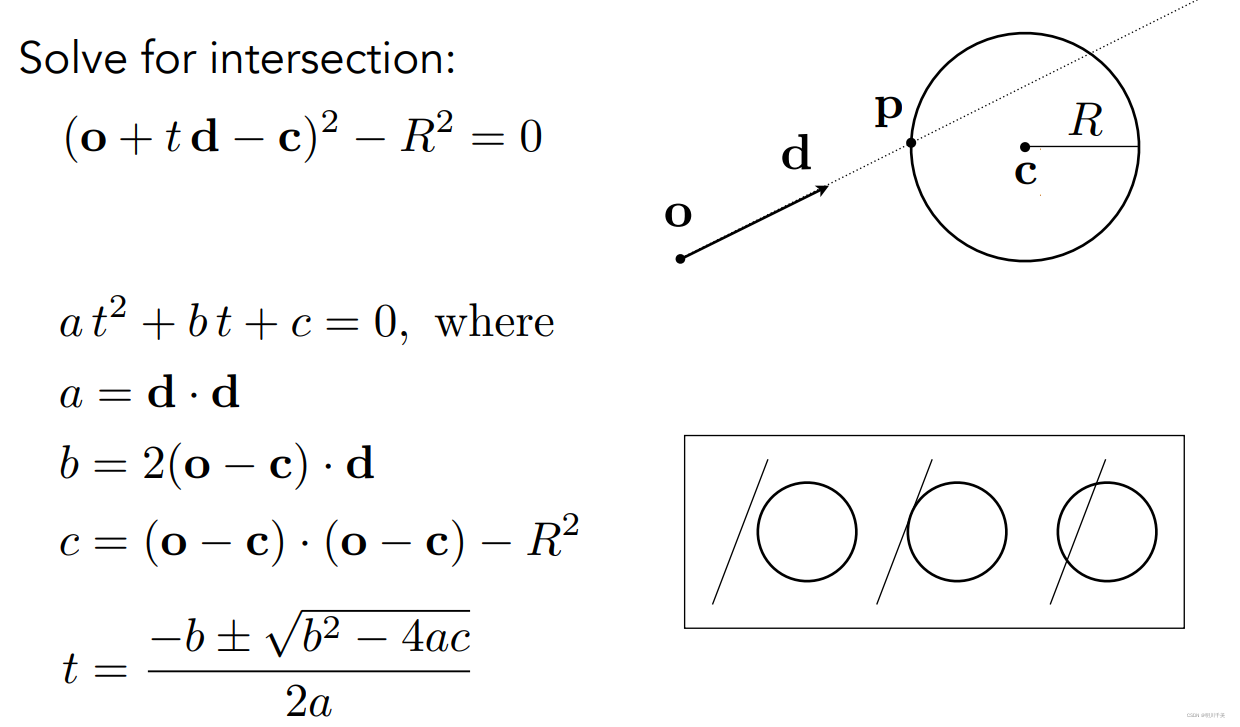
由方程解$t$的数量来判断有几个相交点（0个，1个，2个），若为2个，则取离光线最近的交点。

由此可以推广应用到所有隐式曲面的交点：
表面交点P都可以由物体方程等于0来表示（$f(p)=0$）,然后让光线方程和P点方程联立，解方程即可。

2.4.3计算光线和显式曲面的交点

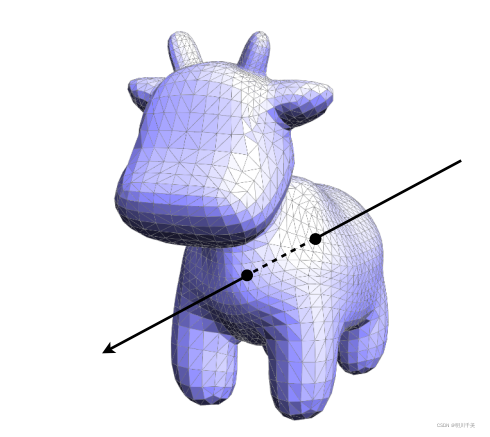
如上图所示，为光线与显式曲面的交点，可以看出，其交点其实就是与三角形面的交点，因此转化问题为计算光线与三角面的交点。

首先先做该三角形所在平面，平面由法向量和平面上的一点定义：

联立光线方程和点P方程，解方程；求得t之后，代入光线方程，就能得到交点了：

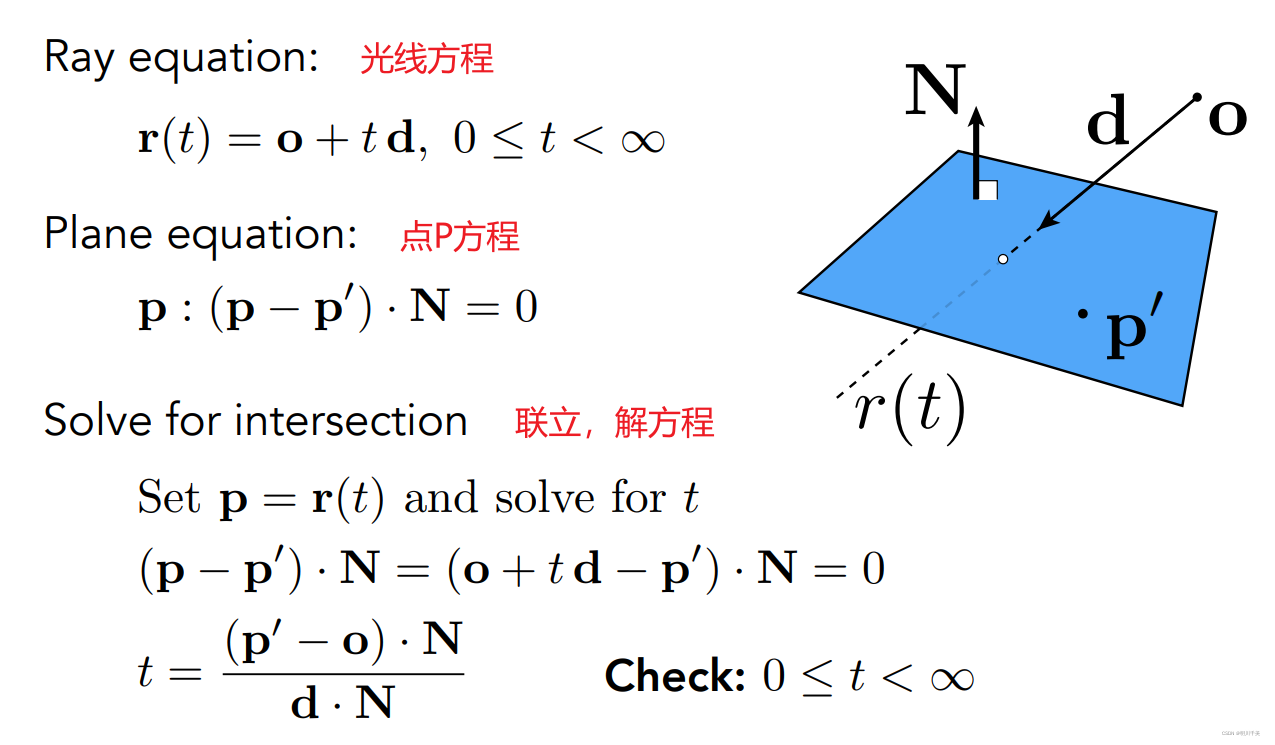
得到了交点之后，就能进一步判断该点是否在三角形内了。
由于判断点是否在三角形内较为麻烦，所以引出新的直接求交点方法
Möller Trumbore 算法：
求解交点位置之后，也顺带判断了该点是否在三角形内部
如上图所示，引用之前所学知识（如何判断平面内一点和三角形的关系），即$a{P}_0+b{P}_1+c{P}_2=P$（其中a+b+c=1；$P_0,P_1,P_2$是三角形的三个顶点；如果该点P位于三角形内部，那么a,b,c均为非负数），因此可以得到图中上方公式。可以将where下的方程代入左侧方程中，解这三个方程即可计算出（t,b1,b2）。

那是这上述所说的计算交点的方法都是非常耗时的，为了能够更快的提高计算交点的速度，我们引入包围盒（Bounding Volumes）概念。