- 1用redis实现的search engine:对标 elasticSearch, solr
- 24K智能处理平台机器视觉行业应用_4k图像实时检测
- 3大数据-11-案例演习-淘宝双11数据分析与预测 (期末问题)
- 4140 基于单片机导盲仪避障语音报警系统设计【毕设课设】_智能导盲仪毕业设计
- 5原来阿里P8的工资这么低啊。。。
- 62024年最全从零开始学习大模型-第一章-大模型是什么,2024年最新【设计思想解读开源框架】_大模型入门
- 7SRA 案例练习:解释 CRUD 矩阵方法,并从上面 “用于化学品跟踪管理系统的 CRUDL 矩阵示例”图中找出被遗漏的需求,并解释是如何找的?_crud矩阵
- 8大模型日报3月19日_clarity upscaler
- 9从零开始:构建你的首个AI绘画ComfyUI工作流_comfyui如何添加 vae节点
- 102024年pmp考试还有多久啊?怎么备考?_2024年pmp考试还有多久?怎么备考?
用C++解决八数码问题(包含讲解和代码)_c++宽度优先算法八数码
赞
踩
前言
将九个数码或一个空格加八个数码放入九宫格内,将顺序打乱后获得一个乱序的九宫格。八数码问题就是指如何通过移动一个格子(下面我将其称为移动元),将乱序的九宫格复原,即通过移动左下图中0的格子,使九宫格恢复成右下图的样子。需要用到搜索求解的方法。
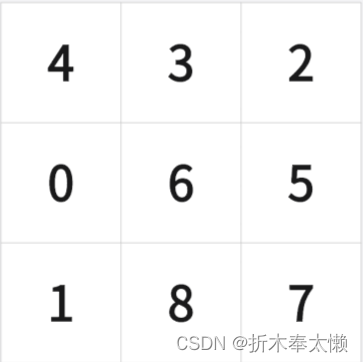
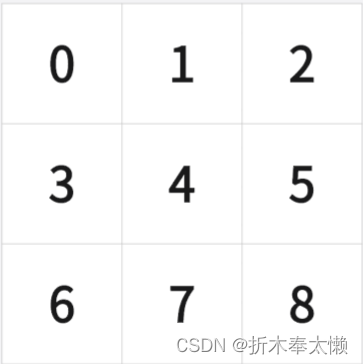
搜索是什么
将乱序的九宫格中0的格子上下左右移动都会得到一个新的格子,在这里我称这个过程为繁殖。每繁殖一次,都将新生的节点作为未繁殖节点存储起来,为下一次繁殖提供选择。而繁殖过的节点作为已繁殖节点存储起来,繁殖出新生节点时遍历所有的已繁殖节点,若新生节点在已繁殖节点中有相同的,则输出此新生节点,避免进入死胡同。在不断繁殖,不断产生新的八数码排序的过程中,程序将找到排序正确的八数码,即找到正解。
需要注意的是,除了第一个节点,即初始八数码,其余所有节点最多只会繁殖出三个节点,因为即使此节点移动元位于中心位置(移动元处于边界的节点只能产生两个或三个子代节点),可以通过上下左右移动移动元繁殖出四个子代节点,其中必有一个与其父节点相同。当繁殖出来的子代节点是已经出现过的节点,此子代节点会被删除,避免八数码再走一遍已经走过的路进入死循环。
而一个节点也可能没有子代,当移动元向可移动的方向移动后产生的子代节点都已经出现过,那么此节点无子代节点,即进入死胡同。
搜索策略
搜索策略即搜索方向,形象来说就是控制下一个繁殖的节点是哪一个。
盲目搜索
盲目搜索有两种,即深度优先和宽度优先。深度优先即节点繁殖出子代后,随机选择其子代中某一节点为当前节点,并繁殖当前节点,再从当前节点的子代中任选一个为当前节点繁殖,只有到当前节点无法产生后代(也就是进入死胡同),当前节点才会回溯到其父代节点,繁殖其他子代节点。广度优先比较形象的解释是一代一代地繁殖,比如将初始节点的子代节点(下面称为二代节点)存储起来,并先将二代节点全部繁殖。将二代节点繁殖出来的三代节点又存储起来,再将三代节点全部繁殖,如此循环下去。
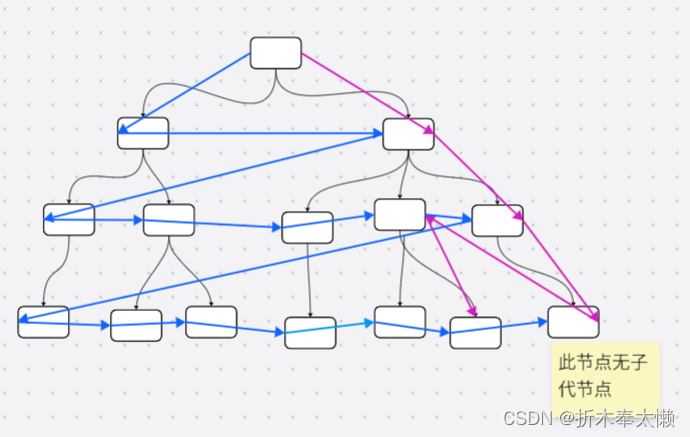
由下图可得,盲目搜索广度优先优先选择代数最小,也就是最早繁殖出来的节点,而深度优先优先选择代数最大的节点,则最晚繁殖出来的节点。当用链存储未繁殖的节点时,链头是最早繁殖的节点,链尾是最晚繁殖的节点,所以使用盲目搜索是用链存储未繁殖节点时很好的选择。
蓝色线为广度优先
紫色线为深度优先
启发式搜索
启发式搜索即为所有的节点加上一个估价函数:,用来推测当前节点还原八数码所需的代价,代价越低则越好。
一般表示当前节点为第几代节点,
表示预估代价。预估函数也有多种计算方式,下面只演示计算曼哈顿距离总和和不在位点两种。启发式搜索即选择所有未繁殖节点中
值最小的进行繁殖。启发式搜索让搜索方向带有选择性,往往可以避开大部分偏离复原八数码的搜索路径,减少运算。
启发式搜索也有两种,可主动回溯和不可主动回溯,类似于盲目搜索的广度优先和深度优先。可主动回溯即每繁殖一次,都遍历一遍所有的未繁殖点,选择估价最低的进行繁殖。不可主动回溯则每繁殖一次,优先从子代节点中选择估价最低的进行繁殖,若不能产生节点,则回溯到其父代节点,繁殖其父代节点的其他节点。
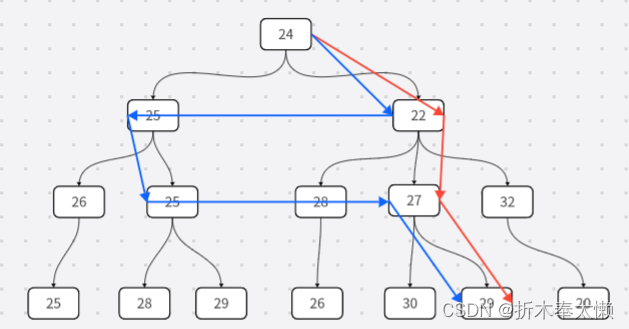
如下图可见,不可主动回溯的搜索方法更偏向于“一条路走到黑”。
红色为不可主动回溯
蓝色为可主动回溯
代码
我在代码中进行了有些扩展,以下的代码中启发式搜索不可回溯的代码设置了步数上限,两份代码也都可以将三阶的八数码改为四阶的十五数码甚至更高阶。
四种搜索策略的代码非常相似,最主要的区别在于对下一个要繁殖的节点的选择。两种盲目搜索中,参照上面的路径图不难发现,盲目搜索广度优先的下一个要繁殖的节点都是最早被繁殖出来的,而盲目搜索深度优先下一个要繁殖的节点时最晚被繁殖出来的。如果用链来按繁殖时间来存储所有的未繁殖节点,比如每繁殖一次都将繁殖出来的节点存储在链的尾部,那么链的头部所存储的节点便是所有未繁殖节点中最早被繁殖出来的,而链尾部的节点则是最晚被繁殖出来的。只要在选择下一个繁殖节点是选择链尾或链首的节点,便可以在同一份代码中分别实现盲目搜索深度优先和盲目搜索广度优先。而启发式搜索可回溯中,每繁殖一次都要在所有的未繁殖节点中选择估价最低的节点,那么只要把刚才所提到的链遍历一遍进行选择即可,因此两种盲目搜索和启发式可回溯搜索的代码很相似,我在下面将这三种搜索方式的代码写在一起。
代码如下:
- #pragma region 非主函数
-
- #include <stdio.h>
- #include <stdlib.h>
- #include <math.h>
- #include <stack>
- #include<queue>
- #include<Windows.h>
- #include<time.h>
- using namespace std;
-
- #define N 3 // 阶数
- #define maxgenerations 500000 //繁殖次数上限
- #define maxmutation 80//八数码初始化时变异次数
- #define interval 1000//演示八数码复原时每帧间隔为多少毫秒
- #define tactics 1 //1:启发式可回溯; 2:盲目广度; 3:盲目深度
- #define mutate false //八数码初始化是否变异
-
- typedef struct Node
- {
- int layer; // (层数)步数
- int forecastvalue;//估价函数中h(x)部分,可为计算不在对应位置的数码数,可为计算曼哈顿距离总和
- //dif为0时即为找到正解
- int inspire; //估价
- int data[N][N]; // 存放棋盘状态
- Node* father;//父节点,用于找到正解后追溯上层节点
- int x0; //数字0的x坐标
- int y0; //数字0的当前y坐标
- }node;
-
- //用于记录已出现过的节点,繁殖时遍历此链表,假若有相同的放弃繁殖
- typedef struct Record {
- Record* prev;
- Node* me; //记录在链表的Node节点
- Record* next; //指向下一个Record节点的尾指针
- }recordd;
-
- Record* record; //记录链
- Record* travel; //用于遍历,判断新生节点是否已出现过
- Record* first; //记录链的头结点
-
- //记录未繁殖节点
- Record* recordnode;
- Record* travelnode;
- Record* firstnode;
- Record* bestnode=NULL;//Record->me估价最低
-
- //在记录链尾部插入节点
- void insertrecord(Node* current) {
- //开辟一个Record节点的内存
- Record* newrecord = (Record*)malloc(sizeof(Record));
- record->next = newrecord;//Record链尾节点的尾指针指向新节点
- record = record->next;//Record尾结点改为新Record节点
- record->me = current;//Record的me存储要填入链表的Node节点
- record->next = NULL;
- }
-
- //在为繁殖节点链尾部插入节点
- void insertrecordnode(Node* current) {
- //开辟一个Record节点的内存
- Record* newrecord = (Record*)malloc(sizeof(Record));
- recordnode->next = newrecord;//Record链尾节点的尾指针指向新节点
- recordnode->next->prev = recordnode;
- recordnode = recordnode->next;//Record尾结点改为新Record节点
- recordnode->me = current;//Record的me存储要填入链表的Node节点
- recordnode->next = NULL;
- }
-
- //从未繁殖节点链删除节点
- void deleterecordnode() {
- if (bestnode->next == NULL) {
- recordnode = recordnode->prev;
- bestnode->prev->next = NULL;
- //printf("no next delete:inspire %d dif %d", bestnode->me->inspire, bestnode->me->dif);
- }
- else {
- bestnode->prev->next = bestnode->next;
- bestnode->next->prev = bestnode->prev;
- //printf("delete:inspire %d dif %d", bestnode->me->inspire, bestnode->me->dif);
-
- }
-
- }
-
- Node* findbestnode() {
- //遍历未繁殖节点链,选择估价最低的
- if (tactics == 1) {
- int bestcost = NULL;
- travelnode = firstnode;
- while (travelnode->next != NULL) {
- travelnode = travelnode->next;
- if (bestcost == NULL || bestcost > travelnode->me->inspire) {
- bestcost = travelnode->me->inspire;
- bestnode = travelnode;
- }
- }
- return bestnode->me;
- }
- //选择未繁殖节点链最接近first的节点,即代数最小的节点,盲目广度优先
- if (tactics == 2) {
- bestnode = firstnode->next;
- return bestnode->me;
- }
- if (tactics == 3) {
- bestnode = recordnode;
- return bestnode->me;
- }
- }
-
- stack<Node*> route;//找到正解后用于储存变换路线
-
- //计算预估代价
- void farecastvalue(Node* p) {
-
- //当manhadon为false时,预估代价为不在位点数
- //当manhadon为true时,预估代价为所有数码的曼哈顿距离总和
- bool manhadon = true;
-
- p->forecastvalue = 0;
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- if (manhadon) {
- p->forecastvalue += abs((p->data[i][j] % N) - j);
- p->forecastvalue += abs(((p->data[i][j] - (p->data[i][j] % N)) / N) - i);
- }
- else {
- if (p->data[i][j] != N * i + j) {
- p->forecastvalue++;
- }
- }
- }
- }
- }
-
- //判断新生节点是否重复
- //遍历record链表,一一与新生节点对照,若有相同,则新生节点已出现过,放弃繁殖
- bool checksame(Node* p) {
-
- travel = first;//用于遍历的travel回归至记录链的头结点
- while (travel != NULL) {
- int check = 0;
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- //新生节点与travel节点相同位置的元素相减,取绝对值总和
- check = check + abs(p->data[i][j] - travel->me->data[i][j]);
- }
- }
- //结果不为零则相同,放弃繁殖,返回true
- if (check == 0) {
- return true;
- }
- //不相同则travel移向记录链的下一个节点
- else {
- travel = travel->next;
- }
- }
- //没有相同则返回false
- return false;
- }
-
- //0向左右上下移动
- void right(Node* s)
- {
- Node* p = (Node*)malloc(sizeof(Node));
-
- if (!p) {
- printf("malloc fail\n");
- return;
- }
-
- //新生节点的父节点为繁殖节点
- p->father = s;
- p->layer = s->layer + 1;
-
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- p->data[i][j] = s->data[i][j];
- }
- }
- p->x0 = s->x0;
- p->y0 = s->y0;
-
- //先判断0是否有移动空间
- if (p->y0 < N - 1) {
- p->data[p->x0][p->y0] = p->data[p->x0][p->y0 + 1];
- p->data[p->x0][p->y0 + 1] = 0;
- p->y0 = p->y0 + 1;//更改0的坐标,容易忽略
- }
- else {
- p = NULL;
- free(p);
- return;
- }
-
- //如果节点已出现过,则清除
- bool f = checksame(p);
- if (f) {
- p = NULL;
- free(p);
- return;
- }
-
- farecastvalue(p);
- p->inspire = p->layer + p->forecastvalue;
-
- insertrecordnode(p);
- }
- void left(Node* s)
- {
- Node* p = (Node*)malloc(sizeof(Node));
-
- if (!p) {
- printf("malloc fail\n");
- return;
- }
-
- p->father = s;
- p->layer = s->layer + 1;
-
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- p->data[i][j] = s->data[i][j];
- }
- }
- p->x0 = s->x0;
- p->y0 = s->y0;
-
- if (p->y0 > 0) {
- p->data[p->x0][p->y0] = p->data[(p->x0)][(p->y0) - 1];
- p->data[p->x0][(p->y0) - 1] = 0;
- p->y0 = p->y0 - 1;
- }
- else {
- p = NULL;
- free(p);
- return;
- }
-
- //如果节点已出现过,则清除
- bool f = checksame(p);
- if (f) {
- p = NULL;
- free(p);
- return;
- }
-
- farecastvalue(p);
- p->inspire = p->layer + p->forecastvalue;
-
- insertrecordnode(p);
- }
- void up(Node* s)
- {
- Node* p = (Node*)malloc(sizeof(Node));
-
- if (!p) {
- printf("malloc fail\n");
- return;
- }
-
- p->father = s;
- p->layer = s->layer + 1;
-
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- p->data[i][j] = s->data[i][j];
- }
- }
- p->x0 = s->x0;
- p->y0 = s->y0;
-
- if (p->x0 > 0) {
- p->data[p->x0][p->y0] = p->data[p->x0 - 1][p->y0];
- p->data[p->x0 - 1][p->y0] = 0;
- p->x0 = p->x0 - 1;
- }
- else {
- p = NULL;
- free(p);
- return;
- }
-
- //如果节点已出现过,则清除
- bool f = checksame(p);
- if (f) {
- p = NULL;
- free(p);
- return;
- }
-
- farecastvalue(p);
- p->inspire = p->layer + p->forecastvalue;
-
- insertrecordnode(p);
- }
- void down(Node* s)
- {
- Node* p = (Node*)malloc(sizeof(Node));
-
- if (!p) {
- printf("malloc fail\n");
- return;
- }
-
- p->father = s;
- p->layer = s->layer + 1;
-
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- p->data[i][j] = s->data[i][j];
- }
- }
- p->x0 = s->x0;
- p->y0 = s->y0;
-
- if (p->x0 < N - 1) {
- p->data[p->x0][p->y0] = p->data[p->x0 + 1][p->y0];
- p->data[p->x0 + 1][p->y0] = 0;
- p->x0 = p->x0 + 1;
- }
- else {
- p = NULL;
- free(p);
- return;
- }
-
- //如果节点已出现过,则清除
- bool f = checksame(p);
- if (f) {
- p = NULL;
- free(p);
- return;
- }
-
- farecastvalue(p);
- p->inspire = p->layer + p->forecastvalue;
-
- insertrecordnode(p);
- }
-
- //繁殖函数(将四个移动函数封装在一起)
- void propagation(Node* s) {
- right(s);
- left(s);
- up(s);
- down(s);
- }
-
- //变异函数(初始化八数码棋盘,将其打乱)
- void bemutation(int detection, Node* p) {
-
- //0向右移
- if (detection == 0) {
- if (p->y0 < N - 1) {
- p->data[p->x0][p->y0] = p->data[p->x0][p->y0 + 1];
- p->data[p->x0][p->y0 + 1] = 0;
- p->y0 = p->y0 + 1;
- }
- }
-
- //左
- if (detection == 1) {
- if (p->y0 > 0) {
- p->data[p->x0][p->y0] = p->data[(p->x0)][(p->y0) - 1];
- p->data[p->x0][(p->y0) - 1] = 0;
- p->y0 = p->y0 - 1;
- }
- }
-
- //上
- if (detection == 2) {
- if (p->x0 > 0) {
- p->data[p->x0][p->y0] = p->data[p->x0 - 1][p->y0];
- p->data[p->x0 - 1][p->y0] = 0;
- p->x0 = p->x0 - 1;
- }
- }
-
- //下
- if (detection == 3) {
- if (p->x0 < N - 1) {
- p->data[p->x0][p->y0] = p->data[p->x0 + 1][p->y0];
- p->data[p->x0 + 1][p->y0] = 0;
- p->x0 = p->x0 + 1;
- }
- }
-
-
-
- }
-
- //打印节点信息
- void print(Node* test) {
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- printf("%2d ", test->data[i][j]);
- }
- printf("\n");
- }
- printf("预估代价:%d; 层数:%d; 移动元在第 %d 行,第 %d 列\n", test->forecastvalue, test->layer, test->x0 + 1, test->y0 + 1);
- }
-
- #pragma endregion
-
- int main() {
-
- srand((unsigned int)time(NULL));
-
- #pragma region 初始化头结点
- Node* root = (Node*)malloc(sizeof(Node));
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- printf("\n请输入第%d行第%d列的数码:", i + 1, j + 1);
- scanf_s("%d", &root->data[i][j], 1);
- getchar();
- if (root->data[i][j] == 0) {
- root->x0 = i;
- root->y0 = j;
- }
- }
- }
- root->layer = 1;
- int a;//0到3之间的随机数,决定初始化棋盘变异方向
- int mutationtimes = 0;//已变异次数
-
- //变异
- if (mutate) {
- while (mutationtimes < maxmutation) {
- a = rand() % 4;
- bemutation(a, root);
- mutationtimes++;
- }
- }
-
- farecastvalue(root);
- root->inspire = root->layer + root->forecastvalue;
- root->father = NULL;
-
- #pragma endregion
-
- bool suscess = false;//是否找到正解
- int generations = 1;//繁殖次数
- Node* current;//当前节点指针
- current = root;//当前节点为root
-
- #pragma region 链的操作
- //存储未繁殖节点的链操作
- recordnode = (Record*)malloc(sizeof(Record));
- recordnode->me = current;
- recordnode->next = NULL;
- recordnode->prev = NULL;
- firstnode = recordnode;
- travelnode = firstnode;
-
- //record为记录已出现节点的链表,first为该链表头节点,travel为遍历节点
- record = (Record*)malloc(sizeof(Record));
- record->me = current;
- record->next = NULL;
- first = record;//记录链表头结点
- travel = first;
-
- #pragma endregion
-
- printf("变异%d次后,初始八数码状态为:\n", mutationtimes);
- print(root);
- printf("\n\n");
- printf("按下回车键开始搜索");
- getchar();
-
- propagation(current);//繁殖初始节点
-
- //搜索循环
- //繁殖次数得到上限跳出循环
- while (generations < maxgenerations) {
-
- generations++;
- printf("%d\n", generations);
-
- current = findbestnode();
- deleterecordnode();
-
- if (current->forecastvalue ==0 ) {
- suscess = true;
- break;
- }
- else {
- propagation(current);
- }
- }
- //搜索循环结束
-
- system("cls");
- if (suscess == true) {
-
- printf("搜索%d次后找到正解\n", generations);
- printf("还原八数码所需步数:%d\n", current->layer);
- while (1) {
- route.push(current);
- //将正解节点以及其所在链前面的所有节点存入route栈
- //此处恰好利用了栈先进后出的特性
- current = current->father;
- if (current->father == NULL) {
- route.push(current);
- break;//到初始节点停止循环
- }
- }
- printf("\n\n\n按下回车键进行演示");
- getchar();
- //逐帧打印route链表上的节点
- while (!route.empty()) {
- Sleep(interval);
- system("cls");
- current = route.top();
- route.pop();
- print(current);
- }
- }
- else {
- printf("! ! ! ! ! S O R R Y ! ! ! ! !\n");
- printf("搜索了%d次,但没找到结果\n\n", maxgenerations);
- printf("\n");
- }
-
- return 0;
- }

启发式不可回溯中,我使用三个栈来存储未繁殖点,代码注释中有讲解,在此不过多赘述。
- #include <stdio.h>
- #include <stdlib.h>
- #include <math.h>
- #include<stack>
- #include<queue>
- #include<Windows.h>
- #include<time.h>
- using namespace std;
-
- #define N 3 // 阶数
- #define maxgenerations 100000 //繁殖次数上限
- #define maxmutation 50//棋盘初始化时变异次数
- #define interval 1000//演示八数码复原时每帧间隔为多少毫秒
- #define mutate true//初始化数码是否自行变异
- #define maxstep 100//步数上限
-
- typedef struct Node
- {
- int layer; // (层数)步数
- int forecastvalue;//预估代价,可为计算不在对应位置的数码数,可为计算曼哈顿距离总和,为0时即为找到正解
- int inspire; //估价
- int data[N][N]; // 存放棋盘状态
- Node* father;//父节点,用于找到正解后追溯上层节点
- int x0; //数字0的x坐标
- int y0; //数字0的当前y坐标
- }node;
-
- //用于储存节点的栈
- stack<Node*> IOS;//缓存区,每繁殖出新的节点先存入此栈,再从中选择估价最低的节点进行繁殖
- stack<Node*> propagule;//IOS中估价最低的节点设为繁殖体,转移到此栈
- stack<Node*> open; // IOS栈非估价最低的节点暂时不繁殖,未繁殖节点存储在此,避免丢失
- stack<Node*> route;//找到正解后用于储存变换路线
- int leastcost = NULL; //记录每一代繁殖时产生子代中最低的估价
-
- /*计算预估代价*/void forcastvalue(Node* p) {
-
- //当manhadon为false时,预估代价为不在位点数
- //当manhadon为true时,预估代价为所有数码的曼哈顿距离总和
- bool manhadon = true;
-
- p->forecastvalue = 0;
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- if (manhadon) {
- p->forecastvalue += abs((p->data[i][j] % N)-j);
- p->forecastvalue += abs(((p->data[i][j] - (p->data[i][j] % N))/N) - i);
- }
- else {
- if (p->data[i][j] != N * i + j) {
- p->forecastvalue++;
- }
- }
- }
- }
- }
-
- /*检查节点是否在当前路径中已出现过*/bool checksame(Node* p) {
- Node* travell;
- travell = p;
- bool same;
- while (travell->father != NULL) {
- same = true;//先假设其为真
- travell = travell->father;
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- if (p->data[i][j] != travell->data[i][j]) {
- same = false;
- }
- }
- }
- //check over
- if (same == true) {
- break;
- }
- }
- return same;
- }
-
- /*繁殖函数*/
- void right(Node* s){
- Node* p = (Node*)malloc(sizeof(Node));
-
- if (!p) {
- printf ("malloc fail\n");
- free(p);
- return;
- }
-
- //新生节点的父节点为繁殖节点
- p->father = s;
- p->layer = s->layer + 1;
- if (p->layer > maxstep) {
- free(p);
- return;
- }
-
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- p->data[i][j] = s->data[i][j];
- }
- }
-
- p->x0 = s->x0;
- p->y0 = s->y0;
- p->data[p->x0][p->y0] = p->data[p->x0][p->y0 + 1];
- p->data[p->x0][p->y0 + 1] = 0;
- p->y0 = p->y0 + 1;
-
-
- //如果节点已出现过,则清除
- bool f = checksame(p);
- if (f) {
- p = NULL;
- free(p);
- return;
- }
-
- forcastvalue(p);
- p->inspire = p->layer + p->forecastvalue;
-
- //leastcost为空或该新生节点的估价比leastcost还小时,更新leastcost
- if (leastcost == NULL || leastcost > p->inspire)
- leastcost = p->inspire;
-
- //若节点被繁殖,先存入IOS区
- IOS.push(p);
- }
- void left(Node* s) {
- Node* p = (Node*)malloc(sizeof(Node));
-
- if (!p) {
- printf("mallocfaile");
- free(p);
- return;
- }
-
- p->father = s;
- p->layer = s->layer + 1;
- if (p->layer > maxstep) {
- free(p);
- return;
- }
-
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- p->data[i][j] = s->data[i][j];
- }
- }
- p->x0 = s->x0;
- p->y0 = s->y0;
- p->data[p->x0][p->y0] = p->data[(p->x0)][(p->y0) - 1];
- p->data[p->x0][(p->y0) - 1] = 0;
- p->y0 = p->y0 - 1;
-
- //如果节点已出现过,则清除
- bool f = checksame(p);
- if (f) {
- p = NULL;
- free(p);
- return;
- }
-
- forcastvalue(p);
- p->inspire = p->layer + p->forecastvalue;
-
- if (leastcost == NULL || leastcost > p->inspire)
- leastcost = p->inspire;
-
- IOS.push(p);
- }
- void up(Node* s) {
- Node* p = (Node*)malloc(sizeof(Node));
-
- if (!p) {
- printf("malloc fail\n");
- free(p);
- return;
- }
-
- p->father = s;
- p->layer = s->layer + 1;
- if (p->layer > maxstep) {
- free(p);
- return;
- }
-
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- p->data[i][j] = s->data[i][j];
- }
- }
- p->x0 = s->x0;
- p->y0 = s->y0;
- p->data[p->x0][p->y0] = p->data[p->x0 - 1][p->y0];
- p->data[p->x0 - 1][p->y0] = 0;
- p->x0 = p->x0 - 1;
-
- //如果节点已出现过,则清除
- bool f = checksame(p);
- if (f) {
- p = NULL;
- free(p);
- return;
- }
-
- forcastvalue(p);
- p->inspire = p->layer + p->forecastvalue;
-
- if (leastcost == NULL || leastcost > p->inspire)
- leastcost = p->inspire;
-
- IOS.push(p);
- }
- void down(Node* s) {
- Node* p = (Node*)malloc(sizeof(Node));
-
- if (!p) {
- printf("malloc fail\n");
- free(p);
- return;
- }
-
- p->father = s;
- p->layer = s->layer + 1;
- if (p->layer > maxstep) {
- free(p);
- return;
- }
-
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- p->data[i][j] = s->data[i][j];
- }
- }
- p->x0 = s->x0;
- p->y0 = s->y0;
- p->data[p->x0][p->y0] = p->data[p->x0 + 1][p->y0];
- p->data[p->x0 + 1][p->y0] = 0;
- p->x0 = p->x0 + 1;
-
- //如果节点已出现过,则清除
- bool f = checksame(p);
- if (f) {
- p = NULL;
- free(p);
- return;
- }
-
- forcastvalue(p);
- p->inspire = p->layer + p->forecastvalue;
-
- if (leastcost == NULL || leastcost > p->inspire)
- leastcost = p->inspire;
-
- IOS.push(p);
- }
- void propagation(Node* s) {
- if (s->y0 < N - 1) //判断是否有移动空间
- right(s);
- if (s->y0 > 0)
- left(s);
- if (s->x0 > 0)
- up(s);
- if(s->x0<N-1)
- down(s);
- }
-
- /*变异函数,用于将初始八数码打乱*/void bemutation(int detection,Node* p) {
-
- //0向右移
- if (detection == 0) {
- if (p->y0 < N - 1) {
- p->data[p->x0][p->y0] = p->data[p->x0][p->y0 + 1];
- p->data[p->x0][p->y0 + 1] = 0;
- p->y0 = p->y0 + 1;
- }
- }
-
- //左
- if (detection == 1) {
- if (p->y0 > 0) {
- p->data[p->x0][p->y0] = p->data[(p->x0)][(p->y0) - 1];
- p->data[p->x0][(p->y0) - 1] = 0;
- p->y0 = p->y0 - 1;
- }
- }
-
- //上
- if (detection == 2) {
- if (p->x0 > 0) {
- p->data[p->x0][p->y0] = p->data[p->x0 - 1][p->y0];
- p->data[p->x0 - 1][p->y0] = 0;
- p->x0 = p->x0 - 1;
- }
- }
-
- //下
- if (detection == 3) {
- if (p->x0 < N - 1) {
- p->data[p->x0][p->y0] = p->data[p->x0 + 1][p->y0];
- p->data[p->x0 + 1][p->y0] = 0;
- p->x0 = p->x0 + 1;
- }
- }
-
-
-
- }
-
- /*打印节点信息*/void print(Node* test) {
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- printf("%2d ", test->data[i][j]);
- }
- printf("\n");
- }
- printf("预估代价:%d; 层数:%d; 移动元在第 %d 行,第 %d 列\n", test->forecastvalue, test->layer, test->x0+1, test->y0+1);
- }
-
- int main() {
-
- srand((unsigned int)time(NULL));
- #pragma region 初始化头结点
- Node* root = (Node*)malloc(sizeof(Node));
- for (int i = 0; i < N; i++) {
- for (int j = 0; j < N; j++) {
- printf("\n请输入第%d行第%d列的数码:", i + 1, j + 1);
- scanf_s("%d", &root->data[i][j],1);
- getchar();
- if (root->data[i][j] == 0) {
- root->x0 = i;
- root->y0 = j;
- }
- }
- }
- root->layer = 1;
-
- int mutationtimes = 0;//已变异次数
- if (mutate) {
- int a;//0到3之间的随机数,决定初始化棋盘变异方向
- while (mutationtimes < maxmutation) {
- a = rand() % 4;
- bemutation(a, root);
- mutationtimes++;
- }
- }
-
- forcastvalue(root);
- root->inspire = root->layer + root->forecastvalue;
- root->father = NULL;
- #pragma endregion
-
- bool suscess = false;//是否找到正解
- int generations = 1;//繁殖次数
- Node* current;//当前节点指针
- current = root;//当前节点为root
- propagation(current);//繁殖初始节点
-
- printf("变异%d次后,初始八数码状态为:\n", mutationtimes);
- print(root);
- printf("\n\n");
- printf("按下回车键开始搜索");
- getchar();
- system("cls");
-
- //搜索循环
- //繁殖次数得到上限跳出循环
- while (generations < maxgenerations) {
- printf("%d\n", generations);
-
- if (open.empty() && IOS.empty() && propagule.empty()) {
- system("cls");
- printf("步数上限太小,不存在解");
- getchar();
- break;
- }
-
- //当leastcost为空,说明待繁殖栈的节点没有繁殖出新节点,即死胡同,此时调用closed栈里的节点
- if (!open.empty()&&leastcost == NULL) {
- current = open.top();
- open.pop();
- propagation(current);
- generations++;
- }
-
- //调用缓存区内节点
- while (!IOS.empty()) {
- current = IOS.top();
- IOS.pop();
-
- //判断是否找到正解
- if (current->forecastvalue == 0) {
- suscess = true;
- break;
- }
-
- //启发式搜索
- //如果当前繁殖体的估价为此一代最小值,则移入待繁殖栈propagule
- if (current->inspire == leastcost) {
- propagule.push(current);
- }
- //如果当前繁殖体的估价不是此一代最小值,则移入未繁殖的节点栈closed
- else {
- open.push(current);
- }
-
-
- }
- //找到正解跳出搜索循环
- if (suscess == true)
- break;
-
- leastcost = NULL;//IOS栈被清空后leastcost变回null
-
- //待繁殖区繁殖体一一繁殖
- while (!propagule.empty()) {
- current = propagule.top();
- propagation(current);
- generations++;
- propagule.pop();
- }
-
- }
-
- system("cls");
- if (suscess == true) {
- printf("变异%d次后,初始八数码状态为:\n", mutationtimes);
- print(root);
- printf("\n");
-
- printf("成功找到正解\n");
- printf("繁殖次数(即搜索次数): %d\n", generations);
- printf("还原八数码所需的步数:%d\n", current->layer);
- while (1) {
- route.push(current);
- //将正解节点以及其所在链前面的所有节点存入route栈
- //此处恰好利用了栈先进后出的特性
- current = current->father;
- if (current->father == NULL) {
- route.push(current);
- break;//到初始节点停止循环
- }
- }
- printf("\n\n\n按下回车键进行演示");
- getchar();
- //逐帧打印route链表上的节点
- while (!route.empty()) {
- Sleep(interval);
- system("cls");
- current = route.top();
- route.pop();
- print(current);
- }
- }
- else {
- printf("! ! ! ! ! S O R R Y ! ! ! ! !\n");
- printf("搜索了%d次,但没找到结果\n\n", generations);
- printf("\n");
- }
-
- return 0;
- }

搜索结果区别
在设定步数上限内是否有解和变异次数的关系
| 步数上限 | 10 | 25 | ||
| 变异次数 | 40次 | 200次 | 40次 | 400次 |
| 有解的概率 | 60% | 10% | 90% | 70% |
不同阶数对搜索结果的影响
| 变异70次后不同阶数数码搜索结果 | |||||
| 3阶 | 4阶 | 5阶 | |||
| 搜索次数 | 步数 | 搜索次数 | 步数 | 搜索次数 | 步数 |
| 6523 | 18 | 4139 | 25 | 31276 | 21 |
| 15 | 11 | 82165 | 31 | 24370 | 21 |
| 2393 | 18 | 8654 | 21 | 4006 | 19 |
| 233 | 17 | 435 | 13 | 23074 | 14 |
| 69 | 13 | 6577 | 24 | 124691 | 35 |
同一初始八数码使用不同搜索法结果(预估代价为计算曼哈顿距离总和):
| 可主动回溯搜索 | 不可主动回溯搜索 | 宽度优先搜索 | 深度优先搜索 | ||||
| 搜索次数 | 步数 | 搜索次数 | 步数 | 搜索次数 | 步数 | 搜索次数 | 步数 |
| 6 | 6 | 4 | 4 | 64 | 6 | >5000000 | \ |
| 4 | 4 | 4 | 4 | 14 | 4 | >5000000 | \ |
| 44 | 10 | 10 | 10 | 5231 | 10 | >5000000 | \ |
| 86 | 12 | 16 | 12 | 26180 | 12 | >5000000 | \ |
| 268 | 16 | 379 | 268 | 2625256 | 16 | >5000000 | \ |
| 96 | 17 | 50 | 39 | 502276 | 17 | >5000000 | \ |
| 3227 | 17 | 75 | 59 | 8933557 | 17 | >5000000 | \ |
| 25855 | 17 | 249 | 165 | 9813260 | 17 | >5000000 | \ |
| 51136 | 26 | 417 | 316 | >50000000 | \ | >5000000 | \ |
| 105118 | 38 | 713 | 899 | >50000000 | \ | >5000000 | \ |
同一八数码使用不同的方法计算预估代价搜索结果(可回溯搜索法):
| 预估代价为不在位点数 | 预估代价为曼哈顿距离总和 | ||
| 搜索次数 | 步数 | 搜索次数 | 步数 |
| 6 | 6 | 6 | 6 |
| 5 | 4 | 4 | 4 |
| 79 | 10 | 44 | 10 |
| 274 | 12 | 86 | 12 |
| 3692 | 16 | 268 | 16 |
| 6134 | 17 | 96 | 17 |
| 32266 | 17 | 3227 | 17 |
| 46209 | 17 | 25855 | 17 |



