- 1通信及信号处理领域期刊影响因子、分区及期刊推荐-2024版_信号处理顶刊
- 2request对象的常用方法_列举request对象的常用方法并解释其作用,至少5个。
- 3用单库自增键来生成id了,后期怎么分库?哎,这个坑大!_自增id后期分表分库怎么处理
- 4基于WinForm的c#上位机制作_基于c#上位机制作(winform控件) | 程序员灯塔
- 5微信小程序自动回复用户消息_微信小程序客服自动回复源码
- 6Python快速无限制使用接口实现AI小说续写:API详解与代码示例_小说网站api
- 7LSTM实现时间序列预测(PyTorch版)_pytorch lstm预测时间序列实战-准备数据
- 8GNN图神经网络的Python实现_gnn python
- 9【uniapp】【微信小程序】微信小程序报错集锦(一)_hidetabbar:fail not tabbar page
- 10springboot中的restTemplate访问get,post请求的各种方式_springboot resttemplate post
百度松果线上菁英班竞赛真题_小码哥最近在玩一个游戏叫做冰雪大冒险,这个游戏在一个n行m列的网格上进行。某些
赞
踩
目录
1.MC0101冰雪大冒险(难度:白银)
题目描述
小码哥最近在玩一个游戏叫冰雪大冒险,这个游戏在一个n行m列的网格上进行。某些格子上 存在一些无法通过的障碍物,其余均是光滑的冰面。
玩家初始在其中一个非障碍物的格子上,且保持静止,然后他会通过操控角色进行上下左右移动,当他控制角色朝一个方向移动时,角色会在冰面上一直滑行。直到角色移动方向的下一个是障碍物或者超出图的边界时,角色才会停止移动,然后等待小码哥的下一个操作。
现在给出地图中所有障碍物的位置,小码哥的初始位置和小码哥的操作序列,请你求出小码哥最终停留的位置。
输入格式
第一行输入两个数n,m(2<=n,m<=100),表示地图的行数和列数。
第二行输入两个整数x,y(1<=x<=n,1<=y<=m),表示小码哥初始时在第x行第y列。
第三行输入一个整数k(1<=k<=n*m-1),表示地图上障碍物的个数。
接下来k行,每行两个数字ai,bi,表示第i个障碍物在第ai行第bi列,保证障碍物不会重叠,而且不会出现在小码哥初始位置上。
最后一行输入一个长度不超过1000,包含LRUD四种字母的字符串,字母第i个字母表示小码哥第i步的运动方向。U表示向上,D表示向下,L表示向左,R表示向右。
输出格式:输出两个整数,用空格隔开,表示小码哥的最终位置。
样例输入
5 5
2 2
6
1 3
1 5
3 4
4 2
5 3
5 5
DRDRULUR
样例输出
1 2
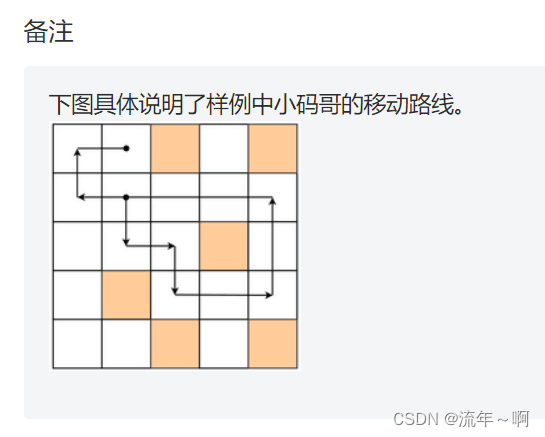
解析:只需要模拟一下即可。
- #include<bits/stdc++.h>
-
- using namespace std;
-
- const int N=110;
-
- int a[N][N];
- int n,m;
- int x,y;
- int t;
-
- string s;
-
- int main()
- {
- cin>>n>>m;
- cin>>x>>y;
- cin>>t;
-
- while(t--)
- {
- int l,r;
- cin>>l>>r;
- a[l][r]=1;
- }
-
- cin>>s;
-
- for(int i=0;i<s.size();i++)
- {
- switch(s[i])
- {
- case 'U':
- while(1)
- {
- if(a[x-1][y]==1||x==1) break;//只要不超过边界或者碰到障碍物,就一直走
- x--;
- }
- break;
- case 'D':
- while(1)
- {
- if(a[x+1][y]==1||x==m) break;
- x++;
- }
- break;
- case 'L':
- while(1)
- {
- if(a[x][y-1]==1||y==1) break;
- y--;
- }
- break;
- case 'R':
- while(1)
- {
- if(a[x][y+1]==1||y==m) break;
- y++;
- }
- break;
- }
- }
-
- cout<<x<<" "<<y<<endl;
-
- return 0;
- }

2.MC0102房间打扫(难度:白银)
题目描述
小码哥准备去打扫一件房间。这个房间可以简单地看成由n行n列,一共n*n个格子组成,每个格子的初始状态要么是干净的,要么是脏的。小码哥打扫房间的方式非常奇怪:如果他打扫了一个脏格子,这个格子就会变得很干净;反之亦然,如果打扫了一个干净的格子,就会变得很脏。
他想从n列的格子中选择几列进行打扫,希望打扫后完全干净的格子的行数尽可能多。注意:如果他选择了一列进行打扫,则它需要打扫这一列所有的格子;一行是干净,是指这一行所有的格子都是干净的。
小码哥并不是很擅长数学,于是希望你计算一下,如果他使用合理的打扫策略,完全打扫干净的行数最多可以有多少。
输入格式
第一行一个整数n(1<=n<=200),表示房间的大小。
接下来n行n列的01串,1表示干净的,0表示脏的。
输出格式
输出一个整数,表示最大可能的完全干净的行数。
样例输入
5
10001
10001
10010
00101
10001
样例输出
3
题解:看似是动态规划问题,实际是让统计哪种行数的状态最多,就拿上述例子来说,最多的初始行数为10001,数目为3,这样,开一个map哈希即可解决。
- #include<bits/stdc++.h>
- #include<map>
- using namespace std;
- const int N=1000;
- char a[N][N];
- map<string,int> mp;
- int main()
- {
- int n;
- cin>>n;
- for(int i=1;i<=n;i++)
- {
- string b="";
- for(int j=1;j<=n;j++)
- {
- cin>>a[i][j];
- b+=a[i][j];
- }
- mp[b]++;
- }
- int ans=0;
- for(map<string,int>::iterator it=mp.begin();it!=mp.end();it++)
- {
- if(ans<it->second)
- ans=it->second;
- }
- cout<<ans;
- return 0;
- }

3.MC0103数字统计(难度:白银)
题目描述
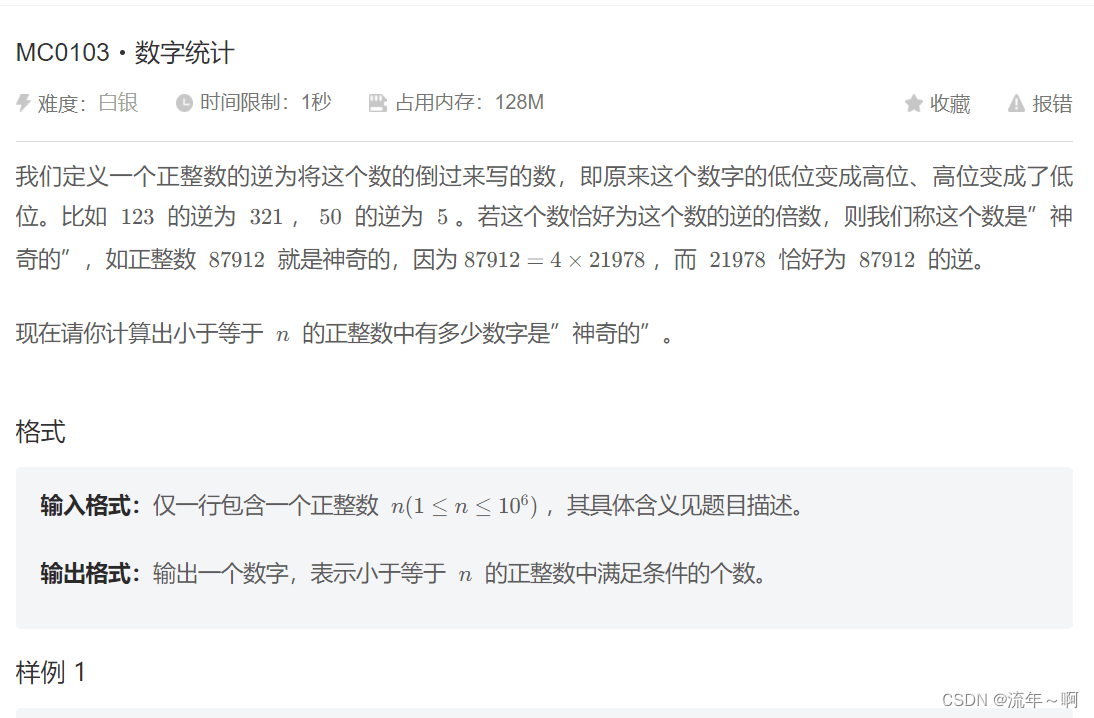
- #include<bits/stdc++.h>
- using namespace std;
- int f(int n)
- {
- int l=n;
- int sum=0;
- while(l)
- {
- sum=sum*10+l%10;
- l/=10;
- }
- if(n%sum==0) return 1;
- return 0;
- }
- int main()
- {
- int n,ans=0;
- cin>>n;
- for(int i=1;i<=n;i++)
- if(f(i)) ans++;
- cout<<ans;
- return 0;
- }

4.MC0104项链(难度:黄金)
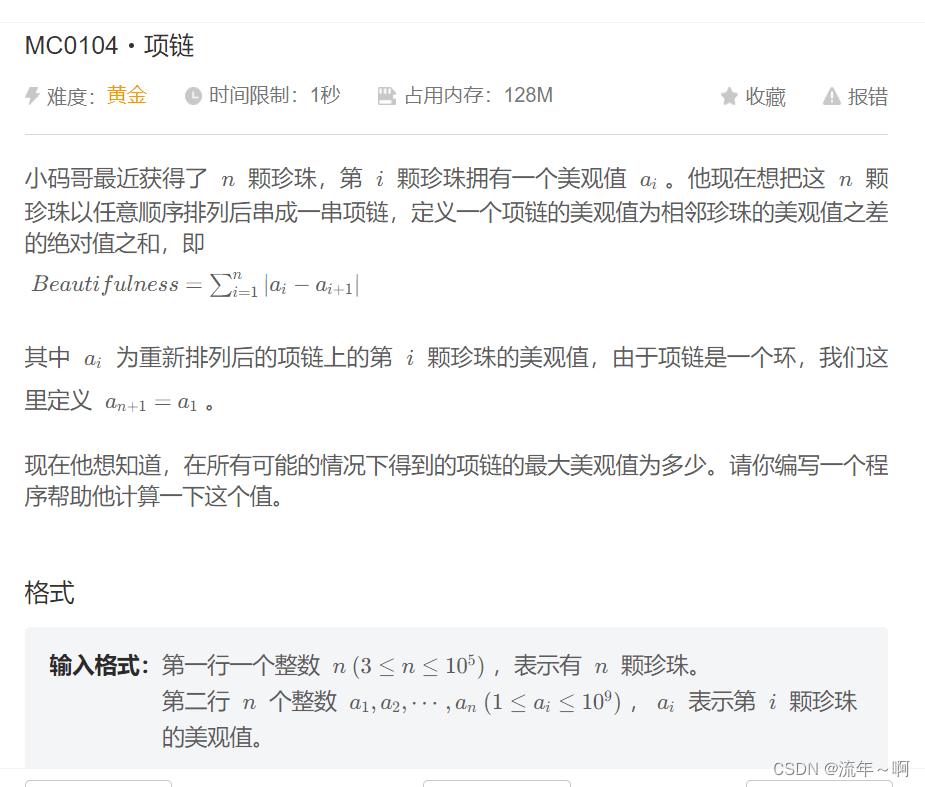

题解:一开始想的是dfs把所有排列都枚举处理,但会TLE,我们不能发现,问题的规模是存在一个序列使得式子成立,我们就拿1 2 3 4,他只存在4 1 3 2 使得式子值最大,规律就是把所有序列排好然后第一个是最大的,第二个是最小的,第三个是第二大的,第四个是第二小的......
- #include<bits/stdc++.h>
- using namespace std;
- const int N=1e6+10;
- int a[N],b[N],vis[N];
- int ans,n;
- int main()
- {
- cin>>n;
- for(int i=1;i<=n;i++)
- cin>>a[i];
- sort(a+1,a+n+1);
- int l=1,r=n;
- int x=0;
- while(l<=r)
- {
- b[++x]=a[r];
- b[++x]=a[l];
- l++;
- r--;
- }
- for(int i=1;i<n;i++)
- {
- int p=b[i]-b[i+1];
- if(p<0) p=-p;
- ans+=p;
- }
- ans+=abs(b[n]-b[1]);
- cout<<ans;
- return 0;
- }

目录
5.函数的幂
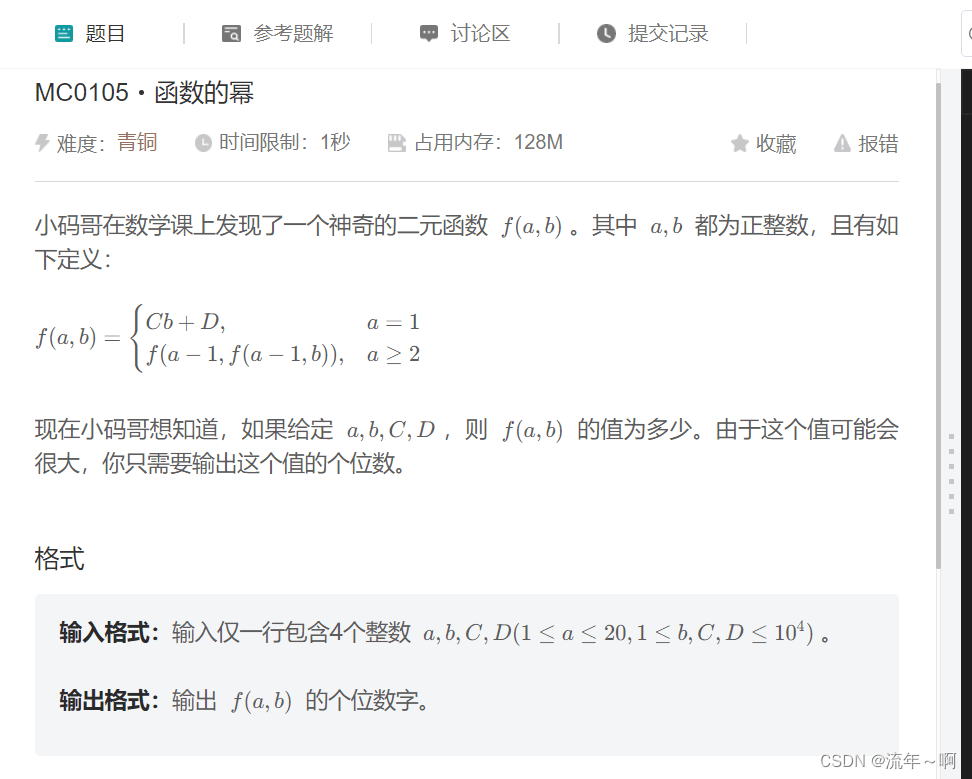
递归函数的调用:
- #include<iostream>
- using namespace std;
- int a;
- int b;
- int C;
- int D;
- int f(int a,int b)
- {
- if(a==1) return (C*b+D)%10;
- return f(a-1,f(a-1,b));
- }
- int main()
- {
- cin>>a>>b>>C>>D;
- cout<<f(a,b);
- return 0;
- }

6.剧场
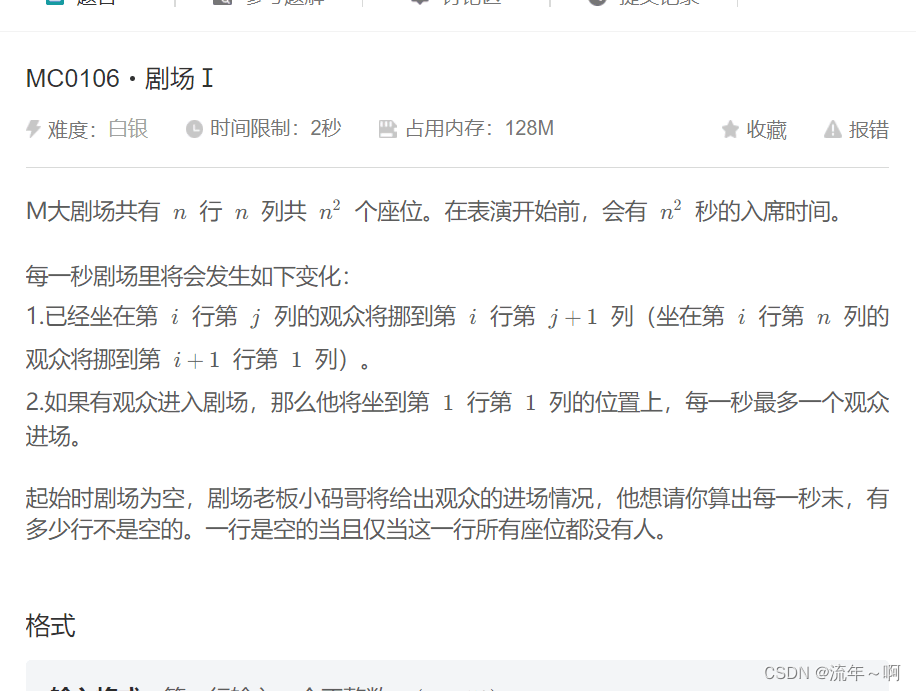
思路: 还是进行模拟,这一题有一个坑,每一秒是先把后面的人都往后移一位,然后才能进入新的人。
- #include<iostream>
- using namespace std;
- const int N=1000;
- char a[N][N];
- int main()
- {
- int n;
- cin>>n;
- int t=n*n;
- //先进行初始化
- for(int i=1;i<=n;i++)
- for(int j=1;j<=n;j++)
- a[i][j]='0';
- while(t--)
- {
- for(int i=n;i>=1;i--)
- {
- for(int j=n;j>=1;j--)
- {
- if(j==1)
- {
- if(a[i][j]=='0'&&a[i-1][n]=='1')
- {
- a[i][j]='1';
- a[i-1][n]='0';
- }
- }
- else
- {
- if(a[i][j]=='0'&&a[i][j-1]=='1')
- {
- a[i][j]='1';
- a[i][j-1]='0';
- }
- }
- }
- }
- char x;
- cin>>x;
- if(x=='1') a[1][1]='1';
- int ans=0;
- for(int i=1;i<=n;i++)
- {
- int sum=0;
- for(int j=1;j<=n;j++)
- {
- if(a[i][j]=='1') sum++;
- }
- if(sum!=0) ans++;
- }
- cout<<ans<<" ";
- }
- return 0;
- }

7.污渍

分析:只需要讨论几种情况即可:包含,相离,相交。
- #include<iostream>
- using namespace std;
- int main()
- {
- int a,b,v1,c,d,v2;
- cin>>a>>b>>v1>>c>>d>>v2;
- int x1=a,y1=b-v1,x2=a+v1,y2=b;
- int x3=c,y3=d-v2,x4=c+v2,y4=d;
- int m1,n1;
- int m2,n2;
- m1=max(min(x1,x2),min(x3,x4));
- n1=max(min(y1,y2),min(y3,y4));
- m2=min(max(x1,x2),max(x3,x4));
- n2=min(max(y1,y2),max(y3,y4));
- if(m2>m1&&n2>n1)
- cout<<v1*v1+v2*v2-(m2-m1)*(n2-n1);//相交
- else
- cout<<v1*v1+v2*v2;//相离
- return 0;
- }

8.白给

- #include<iostream>
-
- using namespace std;
-
- int main()
- {
- int x,y,n;
- cin>>x>>y>>n;
- while(n--)
- {
- if(x>=y)
- {
- int q=x/2;
- x=x-q;
- y=y+q;
- }
- else
- {
- int q=y/2;
- x=x+q;
- y=y-q;
- }
- }
- cout<<x<<" "<<y<<endl;
- return 0;
- }

9.新河妇荡杯
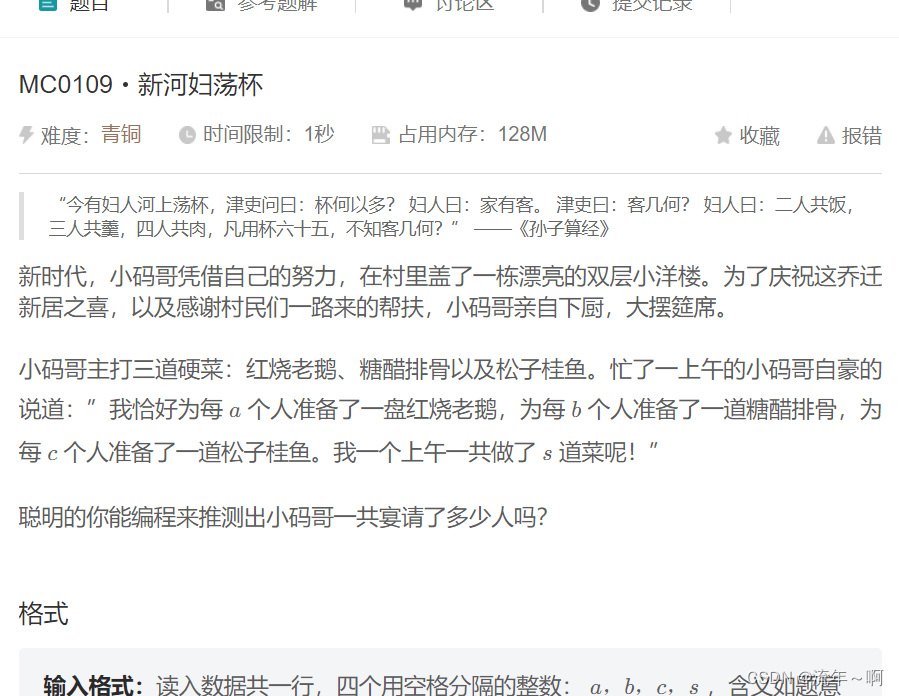
- #include<iostream>
-
- using namespace std;
-
- int main()
- {
- int a,b,c,s;
- cin>>a>>b>>c>>s;
- for(int i=1;;i++)
- {
- if(i/a+i/b+i/c==s)
- {
- cout<<i;
- break;
- }
- }
- return 0;
- }

10.曼哈顿矩阵

思路:找到规律即可,随便枚举一个数,找到四个象限之间和自己的坐标轴关系,如果是n,则它前面一定有 (n-1)!*4个数即可找到规律。
- #include<iostream>
- using namespace std;
-
- int main()
- {
- int x,y;
- cin>>x>>y;
- int n=abs(x)+abs(y);
- int sum=0;
- for(int i=0;i<n;i++)
- sum+=i;
- sum*=4;
- int ans=0;
- if(x>=1&&y>=0) ans=x;
- else if(x>=0&&y<0) ans=x-2*y;
- else if(x<=-1&&y<=0) ans=2*n-x;
- else if(x<=0&&y>0) ans=2*n+2*y-x;
- cout<<ans+sum;
- return 0;
- }



