聚类分析个人笔记（未完）_记录在环境配置及聚类分析过程中遇到的问题及个人体会。

前言

聚类的对象有两种，一是对样本进行聚类（Q型聚类），二是对变量进行聚类（R型聚类）；
聚类的方法大体上有五种类型，分别是基于划分、层次、密度、网格、模型的聚类（根据参考文献0）

1、K均值聚类

参考文献1
参考文献2

K均值聚类属于“基于划分的聚类”中的一种，根据文献0：

文献1中的例子非常形象地说明了K均值聚类的原理，结合文献2中对该方法优劣特点的总结：

以及其他文献中提到的：

其他注意事项：

关于K值选取的方法暂时不太懂，先搁置一下。不过根据SPSS的PDF，说的是如果事先能确定要聚成的类数数量，方可使用K-means聚类。但我们是否可以根据聚类输出的一些观测结果，来判断本次聚类的数量，以及初始聚类中心的选择是否合理呢？

SPSS的实现很简单，参照PDF教程来就行了，不过有一点值得注意的是：

在该对话框中，勾上ANOVA表后会输出一个方差分析表

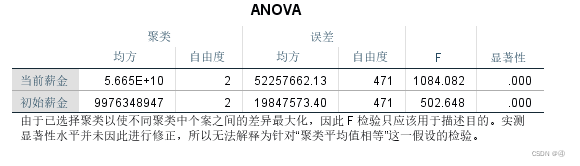
当前薪金和初始薪金是本例中作为聚类依据的两个变量，该表的意义为：

按照方差分析的原理，聚类均方对应的就是组内均方（组内误差平方和/df），误差均方对应组间均方（组间误差平方和/df）

1.1 K-modes与K-prototype

k-means是针对数值型数据进行聚类，而k-modes是针对离散型（分类）数据进行聚类。两种算法的基本思想是一致的，区别在于计算每个样本与簇中心点的距离时，k-means用的是欧式距离（即常规的开根号），而k-modes用的是哈密顿（或称为汉明）距离。
以下来自GPT：

关于哈密顿距离的解释：

很好理解，也就是说如果两个样本在三个特征上的取值不同，则d=3，若在四个特征上取值不同，则d=4…以此类推。
还有一点不一样的在上面有提到，k-modes的簇中心是根据各个特征的众数来确定的。
————————————————————————————————————————————

至于K-prototype则是用于处理数值型和分类型特征都有的数据，具体见GPT：

不过混合距离的计算直接相加似乎有点太粗暴了，我就这一问题又问了GPT：

此外，在其他文章中有看到会在哈密顿距离的前面加一个权重系数：

此处就不深究了，先了解到这个程度就好。

2 聚类效果的检验方法

参考文献3
参考文献4
参考文献5
对于前文中提出的疑问：

我们是否可以根据聚类输出的一些观测结果，来判断本次聚类的数量，以及初始聚类中心的选择是否合理呢？

进一步地，我们想要知道本次聚类的效果如何。上方的方差分析表可以起到一定的作用，让我们知道目前聚出来的几个类别之间的差异是否显著，但这还是远远不够的——假如说选择了不同的初始聚类中心，在同样的显著性水平下都是显著的，那到底哪一种更好呢？通过看F值的大小吗？；以及，类别之间的差异足够大，就能说明聚类效果很好吗？

基于上述的疑问，我们来看文献3和文献4。
文献3提到，评估的指标分为内部评估和外部评估两种类型。

2.1 聚类的可行性检验（聚类趋势评估）

在数据上应用任何聚类算法前，一个重要问题是，即使数据不包含任何集群，聚类方法也会返回群集。换句话说，如果盲目地在数据集上应用聚类算法，它也会将数据划分为聚类，因为这是它应该执行的。
因此，评估数据集是否包含有意义的聚类（即：非随机结构）有时会变得有必要。
此过程被定义为 聚类趋势的评估 或 聚类可行性的分析。
而通常，与非随机结构相对的是均匀分布，霍普金斯统计量的计算原理，便是检查数据是否符合均匀分布。

进行聚类趋势评估通常是利用霍普金斯统计量，具体操作方法可见：文献6

简单解释一下，就是在样本空间中随机抽取n个点，计算每个点在整个样本空间中与距离自己最近的点的距离，然后将其累加得到Σxi；第二步就是在同样的定义域内，但是是根据均匀分布来抽取n个点，计算每个点与距离自己最近的点的距离，然后累加得到∑yi；第三步，我们就可以计算上图公式中的H了，∑yi作为均匀分布，既不会过于分散也不会过于集中，处于一个中间值的状态，假如样本也是接近均匀分布，那么H=0.5；假如样本非常分散，样本点之间的距离就会很大，∑xi也会远大于∑yi，从而让H→0；反之，如果样本很集中，H→1。通常我们可以认为，当 H 高于0.75表示在90%的置信水平下，数据集中存在聚类趋势。

2.2 外部评估指标

（等等，既然已经有少量的标注数据，知道真实标签的情况下，那还能称作是无监督学习吗？