【图】使用邻接表判断有向图和无向图中是否有环（Java 实现）_如何用邻接数组判断是否成环

需求

判断给定的图中是否有环
本文研究有向图及无向图两种情况

分析

1、 当图中边的数量大于节点数量时，必然存在环；
2、 当图中边的数量小于等于节点是，不一定存在环。

下文只讨论第二种情况。

示例及解决方案

如下图是一个具有5个节点的无向图，其关系如下。

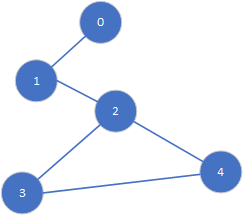
GraphUtil 工具类代码

import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;
import java.util.List;
import java.util.Map;
import java.util.Set;

import org.apache.commons.lang.StringUtils;

/**
 * @Description:判断无向图是否有环 深度优先遍历 需要保存父节点
 */
public class GraphUtil {
	public static void main(String[] args) {
		Set<EdgeRef> graph = buildData();
		boolean haveLoop = GraphUtil.isHaveLoop(graph);
		System.out.println(haveLoop);
	}

	// 创建邻接表
	private  static Set<EdgeRef> buildData() {
		Set<EdgeRef> refs = new HashSet<>();
		refs.add(EdgeRef.of("0", "1"));
		refs.add(EdgeRef.of("1", "2"));
		refs.add(EdgeRef.of("2", "3"));
		refs.add(EdgeRef.of("3", "4"));
		refs.add(EdgeRef.of("2", "4"));
		return refs;
	}

	/**
	 * @param graph  图的邻接边
	 * @param n 图的节点个数
	 * @return 是否存在环
	 */
	public static boolean isHaveLoop(Set<EdgeRef> graph) {
		// 习惯上转换成临接表的形式
		Map<String,List<String>> adj = new HashMap<String, List<String>>();
		for (EdgeRef edg : graph) {
			String node1 = edg.getId();
			String node2 = edg.getRefId();
			if (adj.get(node1) == null) {
				adj.put(node1, new ArrayList<>());
			}
			if (adj.get(node2) == null) {
				adj.put(node2, new ArrayList<>());
			}
			adj.get(node1).add(node2);
			adj.get(node2).add(node1);
		}
		
		// 定义一个节点状态数组 判断是否访问过
		Map<String,Boolean> visited = new HashMap<>();
		Set<String> keySet = adj.keySet();
		for(String key: keySet){
			visited.put(key, false);
		}
		// 引用传递 函数内部修改值后退出函数可见
		int[] a = { 0 };
		for (String key: keySet) {
			// 如果没有进行访问 则进行深度优先搜索回溯
			if (visited.get(key) == false) {
				dfsCycle(adj, key, "", visited, a);
				// 只要有一次i循环时存在环路那就直接提前返回，说明存在环
				if (a[0] == 1) {
					return true;
				}
			}
		}
		return a[0] == 1;
	}

	/**
	 * @param adj 图的临接表
	 * @param current  当前节点
	 * @param parent 父节点
	 * @param visited  判断是否访问
	 * @param flag 是否存在环
	 */
	private static void dfsCycle(Map<String,List<String>> adj, String current, String parent, Map<String, Boolean> visited, int[] flag) {
		// 首先 访问当前节点 并进行标记
		visited.put(current,true);
		// 获取到当前节点能够到达的所有节点
		List<String> list = adj.get(current); 
		for (String can : list) {
			// 如果节点没有被访问过
			if (visited.get(can) == false) {
				// 当前节点就是父节点，循环的节点就是子节点
				dfsCycle(adj, can, current, visited, flag);
			} 
			// 在节点被访问过的情况下 如果该节点不等于父节点 ，说明有环
			else if (!StringUtils.equals(can, parent)) {
				flag[0] = 1;
			}
			// 循环节点等于父节点的情况直接跳过，不用处理
//			else{
//				
//			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101

边对象

public class EdgeRef {

	private String id;
	private String refId;

	public String getId() {
		return id;
	}

	public void setId(String id) {
		this.id = id;
	}

	public String getRefId() {
		return refId;
	}

	public void setRefId(String refId) {
		this.refId = refId;
	}

	public EdgeRef(String id, String refId) {
		super();
		this.id = id;
		this.refId = refId;
	}

	public static EdgeRef of(String id, String refId) {
		return new EdgeRef(id, refId);
	}

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

有向图

有向图求是否有环与无向图类似，其邻接边、DFS、图是否有环算法分别如下：

构建有向邻接表

	/**
	 * 构建 有向图 邻接表
	 * @return
	 */
	public static Map<String,List<String>> builDGAdj(Set<StructRef> graph){

		Map<String,List<String>> adj = new HashMap<String, List<String>>();
		if(Objects.isNull(graph) || graph.isEmpty()){
			return adj;
		}
		for (StructRef edg : graph) {
			String node1 = edg.getId();
			String node2 = edg.getRefId();
			if (adj.get(node1) == null) {
				adj.put(node1, new ArrayList<>());
			}
			if (adj.get(node2) == null) {
				adj.put(node2, new ArrayList<>());
			}
			adj.get(node1).add(node2);
		}
		return adj;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

DFS 判断是否有环

/**
	 * @param adj 图的临接表
	 * @param current  当前节点
	 * @param parent 父节点
	 * @param visited  判断是否访问
	 */
	private static boolean dgDfsCycle(Map<String,List<String>> adj, String current, String parent, Map<String, Boolean> visited,Stack<String> visitedStack) {
		// 首先 访问当前节点 并进行标记
		visited.put(current,true);
		visitedStack.push(current);
		
		// 获取到当前节点能够到达的所有节点
		List<String> list = adj.get(current); 
		for (String can : list) {
			// 如果节点没有被访问过
			if (!visited.get(can)) {
				// 当前节点就是父节点，循环的节点就是子节点
				return dgDfsCycle(adj, can, current, visited,visitedStack);
			} 
			// 在节点被访问过的情况下 说明有环
			else {
				return visitedStack.contains(can);
			}
		}
		return false;
	}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

判断有向图中是否有环

/**
	 * 有向图中判断是否有环
	 * 
	 * @param graph  图的连接边
	 * @param n 图的节点个数
	 * @return 是否存在环
	 */
	public static boolean dGHaveLoop(Set<StructRef> graph) {
		// 习惯上转换成临接表的形式
		Map<String,List<String>> adj = builDGAdj(graph);
		// 定义一个节点状态数组 判断是否访问过
		Map<String,Boolean> visited = new HashMap<>();
		Stack<String> visitedStack = null;
 		Set<String> keySet = adj.keySet();
		for(String key: keySet){
			visited.put(key, false);
		}
		// 引用传递 函数内部修改值后退出函数可见
		for (String key: keySet) {
			visitedStack = new Stack<>();
			// 如果没有进行访问 则进行深度优先搜索回溯
			if (!visited.get(key)) {
				boolean dfs = dgDfsCycle(adj, key, "", visited,visitedStack);
				if(dfs){
					return true;
				}else{
					visited.put(key, false);
					visitedStack.pop();
				}
			}
		}
		return false;
	}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34