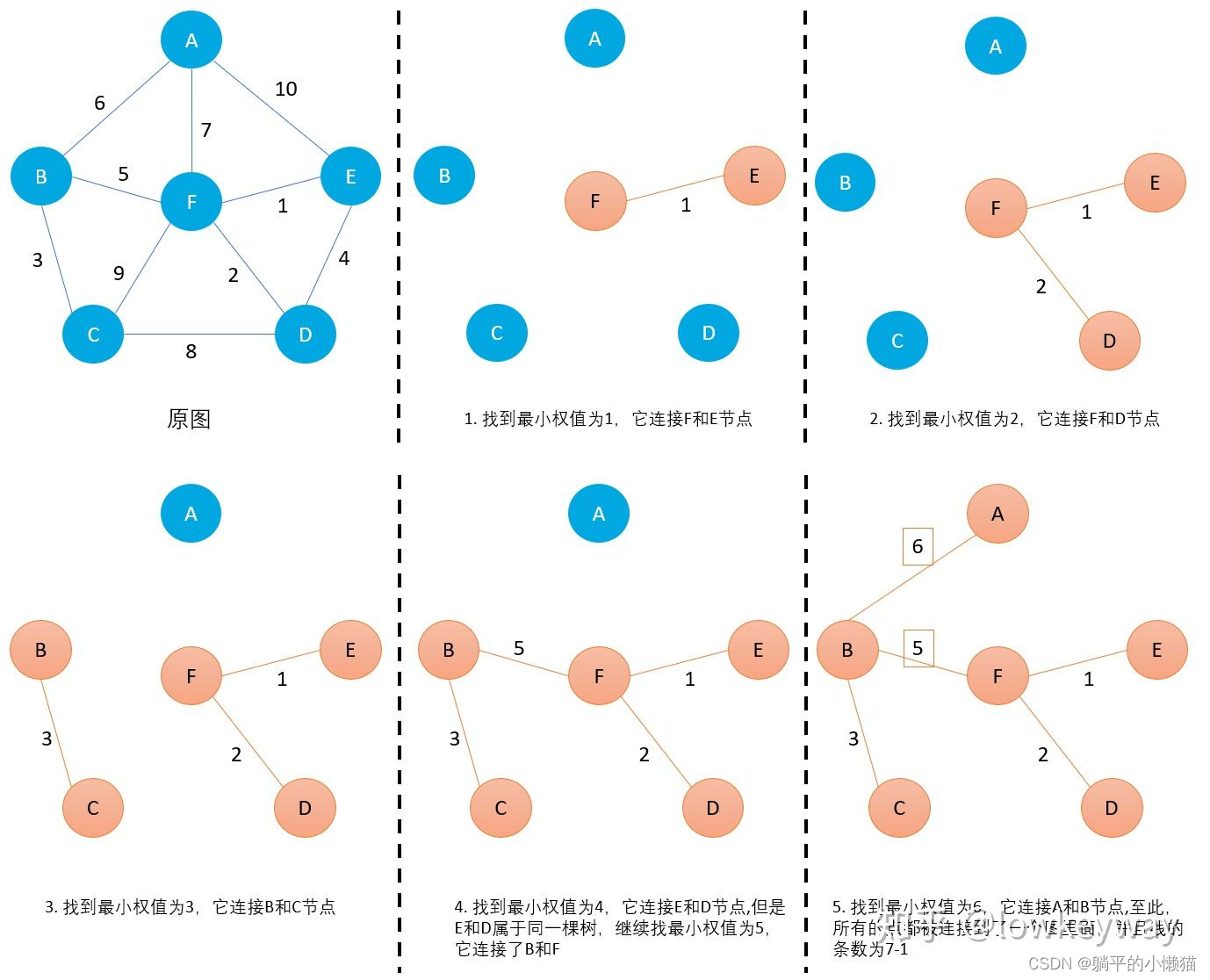
数据结构与算法之最小生成树算法_生成树边的最大权值达到最小算法设计

最小生成树算法是求加权连通图的一种算法，它可以找出一个连通子图，使得子图中所有边的权值之和最小。最小生成树算法的主要应用是在网络设计、公路规划、电力管网规划等领域。

算法步骤：

1. 首先选定任意一个结点作为起点，将该结点加入生成树中。

2. 查找与已加入生成树中结点最近的未加入的结点，将该结点和与其相连的边加入到生成树中。

3. 重复步骤2，直到所有结点均已加入生成树中为止。

算法实现：

最小生成树算法的实现方法有多种，其中比较常见的有Prim算法和Kruskal算法。

1. Prim算法

Prim算法从一个任意选定的起点开始，将该点加入生成树中，同时将该点能到达的所有点的边都加入到一个集合中。然后在这个集合中选择权值最小的边所连接的点，将该点加入生成树中，并将该点能到达的所有点的边都加入到集合中。以此类推，直到所有点都加入到生成树中。

2. Kruskal算法

Kruskal算法先将所有的边按权值从小到大排序，然后从小到大依次选择每一条边。如果这条边的两个端点已经在同一个集合中，则该边不会加入到生成树中；否则将该边加入到集合中，并将这两个端点所在的集合合并成一个集合。重复此操作，直到所有点都加入到生成树中。

无论是Prim算法还是Kruskal算法，都可以在O(E log V)的时间内求出最小生成树。其中，E为边的数量，V为结点的数量。

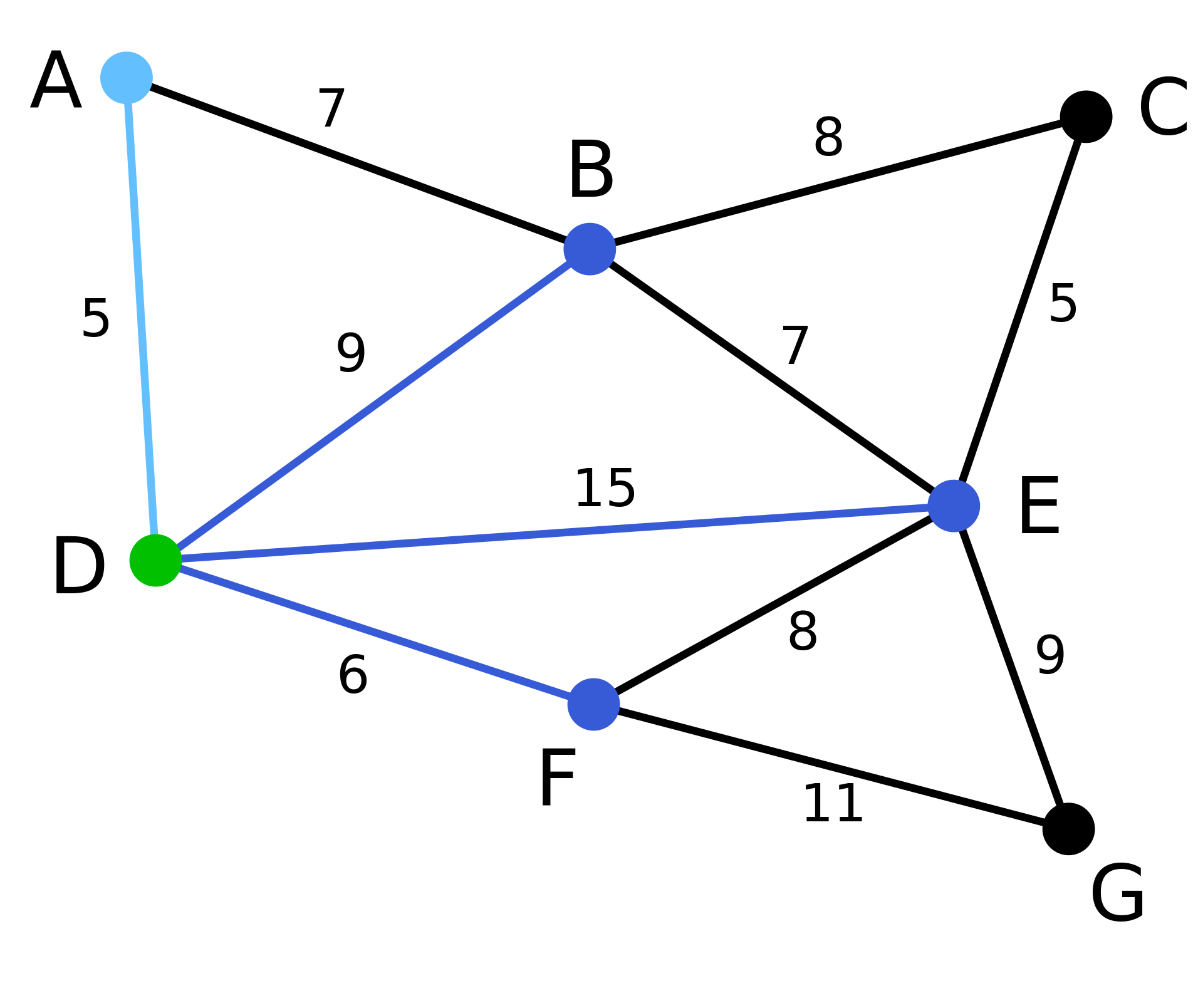
一、C 实现最小生成树算法及代码详解

最小生成树（Minimum Spanning Tree，简称 MST）是求一个带权无向连通图的所有生成树中，边的权值和最小的一棵生成树。常用的算法有Prim算法和Kruskal算法。

下面是 C 语言实现 Prim 算法的代码及详细注释。

#include<stdio.h>
#include<stdlib.h>
#include<limits.h>

#define MAX_VERTEX_NUM 1000      // 图的最大顶点数
#define INF INT_MAX             // 定义正无穷

typedef struct{
    int numVertex;              // 顶点数目
    int numEdge;                // 边的数目
    int edge[MAX_VERTEX_NUM][MAX_VERTEX_NUM];    // 邻接矩阵，存储边的权重
}Graph;

void Prim(Graph *G){
    int lowcost[MAX_VERTEX_NUM];     // 从V中某个点出发到其他点的最小距离集合
    int closest[MAX_VERTEX_NUM];    // 记录最小距离点的编号
    int visited[MAX_VERTEX_NUM];    // 顶点是否被访问的标记
    int i, j, k, min;

    // 初始化 visited 数组，最开始都为未访问
    for(i = 0; i < G->numVertex; i++)  
        visited[i] = 0;

    // 初始化距离数组和 closest 数组，从顶点 0 出发到其他点的距离
    for(i = 1; i < G->numVertex; i++){
        lowcost[i] = G->edge[0][i];   
        closest[i] = 0;
    }

    visited[0] = 1;        // 从 0 号点开始
    for(i = 1; i < G->numVertex; i++){
        min = INF;          // 找到到其他点最近的点（最小权值），同时标记为已访问
        for(j = 1; j < G->numVertex; j++){
            if(!visited[j] && lowcost[j] < min){
                min = lowcost[j];
                k = j;      // 记录最小的边所连的顶点编号
            }
        }
        visited[k] = 1;        // 标记顶点为已访问

        // 更新从V中某个点出发到其他点的最小距离集合和 closest 数组
        for(j = 1; j < G->numVertex; j++){
            if(!visited[j] && G->edge[k][j] < lowcost[j]){
                lowcost[j] = G->edge[k][j];
                closest[j] = k;
            }
        }
    }

    // 输出最小生成树
    int sum = 0;            // 总权值
    for(i = 1; i < G->numVertex; i++){    
        printf("%d - %d: %d\n", closest[i], i, G->edge[closest[i]][i]);
        sum += G->edge[closest[i]][i];      // 累加边的权值
    }
    printf("总权值: %d\n", sum);
}

int main(){
    Graph G;

    // 输入图的顶点数和边的数目
    printf("请输入图的顶点数和边的数目: ");
    scanf("%d%d", &G.numVertex, &G.numEdge);

    // 输入图的边的信息
    for(int i = 0; i < G.numVertex; i++){
        for(int j = 0; j < G.numVertex; j++){
            G.edge[i][j] = INF;
        }
    }
    printf("请依次输入每条边所连的两个顶点和边的权值:\n");
    for(int i = 0; i < G.numEdge; i++){
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        G.edge[u][v] = G.edge[v][u] = w;
    }

    Prim(&G);    // 调用 Prim 算法求解最小生成树

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

主要涉及的算法流程：

1. 初始化 visited 数组，默认都是未访问状态；
2. 初始化 lowcost 数组和 closest 数组，从顶点 0 出发到其他点的距离；
3. 标记顶点 0 为已访问状态，并从剩下的顶点中找到距离顶点 0 最近的顶点，标记为已访问；
4. 更新距离数组和 closest 数组，将新加入已访问集合的顶点 k 的信息加入集合中；
5. 重复第 3 步和第 4 步，直到所有顶点都被访问；
6. 输出最小生成树。

代码中定义的 INF 表示正无穷，即两个点之间没有直接连通的边，用来表示它们之间的距离无穷大。

Prim 算法与 Dijkstra 算法有很多相似之处，两者的区别在于目标不同：Dijkstra 算法是求从起点到其他所有点的最短路径，而 Prim 算法是求一颗最小生成树。

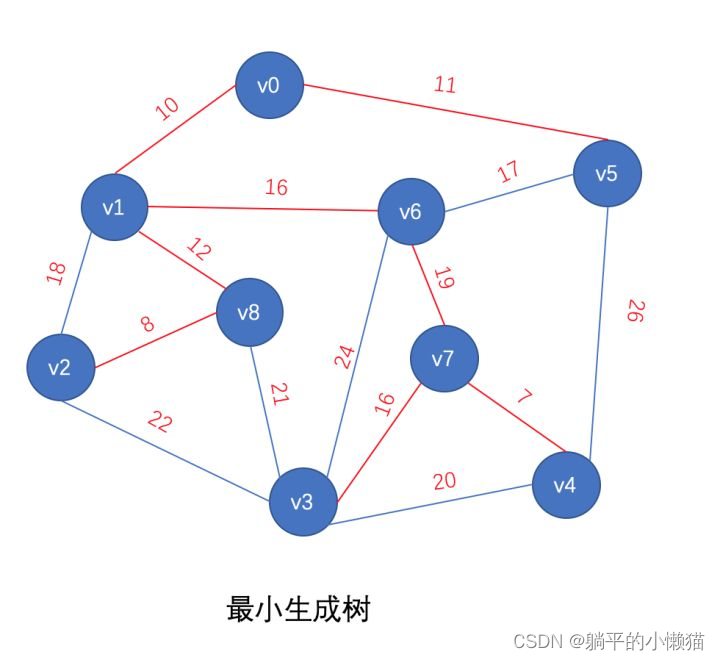
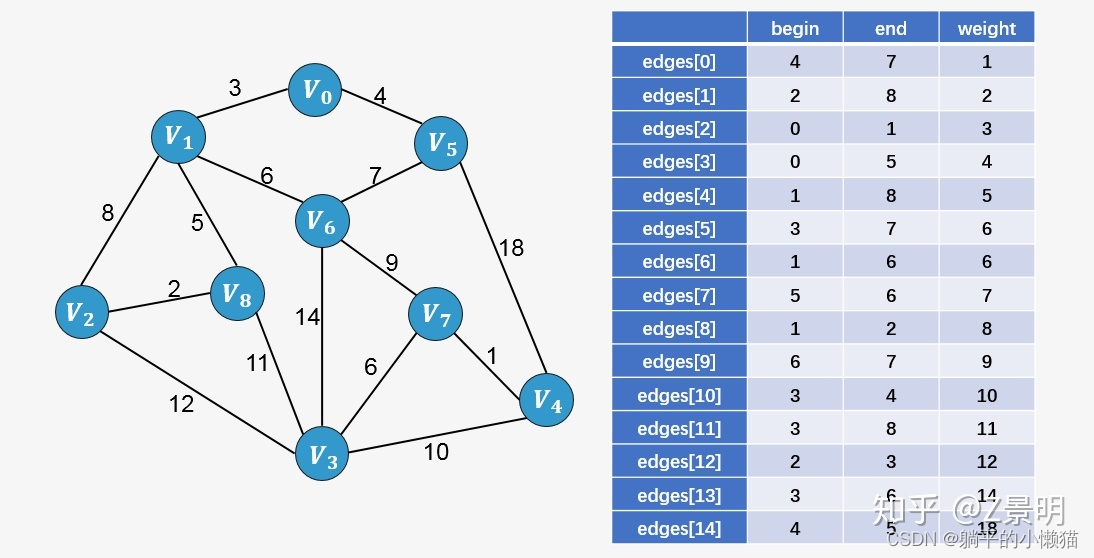
二、C++ 实现最小生成树算法及代码详解

最小生成树算法是图论中的经典问题，它的目标是在给定的带权连通图中找到一棵生成树，使得这棵生成树的总权值最小。常见的最小生成树算法有 Prim 算法和 Kruskal 算法。

本文将详细介绍 Prim 算法和 Kruskal 算法的实现方法，并提供 C++ 代码。

1. Prim 算法

Prim 算法是一种贪心算法，它是从一个顶点开始不断扩展生成树的边，直到生成一棵包含所有顶点的树。具体实现中，Prim 算法使用了一个优先队列来管理候选的边，每次从队列中选择权值最小的边加入生成树。

以下是 Prim 算法的 C++ 代码实现：

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>

using namespace std;

const int MAXN = 1000;  // 最大顶点数
const int INF = 0x3f3f3f3f;  // 无穷大

struct Edge {
    int u, v, w;
    Edge(int u = 0, int v = 0, int w = 0): u(u), v(v), w(w) {}
    bool operator<(const Edge& e) const {  // 用于优先队列的比较运算符
        return w > e.w;
    }
};

vector<Edge> edges[MAXN];  // 存边
bool visited[MAXN];  // 记录顶点是否已经在生成树中
int dist[MAXN];  // 记录生成树到每个顶点的最短距离
int parent[MAXN];  // 记录生成树中每个顶点的父节点

void prim(int s, int n) {  // s 表示起点，n 表示顶点数
    priority_queue<Edge> pq;  // 定义优先队列
    memset(dist, INF, sizeof(dist));  // 初始化距离数组
    memset(visited, false, sizeof(visited));  // 初始化访问记录数组
    memset(parent, -1, sizeof(parent));  // 初始化父节点数组
    dist[s] = 0;  // 初始化起点的距离为 0
    pq.push(Edge(-1, s, 0));  // 将起点加入优先队列
    while (!pq.empty()) {
        int u = pq.top().v; pq.pop();
        if (visited[u]) continue;
        visited[u] = true;
        for (auto& e : edges[u]) {  // 遍历 u 的所有邻接边
            int v = (e.u == u ? e.v : e.u);
            if (!visited[v] && dist[v] > e.w) {  // 如果 v 未访问过且经过 u 到达 v 比原始距离更优
                dist[v] = e.w;
                parent[v] = u;
                pq.push(e);
            }
        }
    }
}

int main() {
    int n, m;
    cin >> n >> m;  // 输入顶点数和边数
    for (int i = 0; i < m; i++) {
        int u, v, w;
        cin >> u >> v >> w;  // 输入一条边
        edges[u].push_back(Edge(u, v, w));  // 存储边
        edges[v].push_back(Edge(v, u, w));
    }

    prim(1, n);  // 假设从节点 1 开始构建生成树

    for (int i = 1; i <= n; i++) {
        cout << i << " " << parent[i] << endl;  // 输出每个节点的父节点
    }

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

2. Kruskal 算法

Kruskal 算法也是一种贪心算法，它首先将所有边按照权值从小到大排序，然后依次从小到大加入边，直到生成一棵包含所有顶点的树为止。具体实现中，Kruskal 算法使用了并查集来维护连通性。

以下是 Kruskal 算法的 C++ 代码实现：

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

const int MAXN = 1000;  // 最大顶点数
const int INF = 0x3f3f3f3f;  // 无穷大

struct Edge {
    int u, v, w;
    Edge(int u = 0, int v = 0, int w = 0): u(u), v(v), w(w) {}
    bool operator<(const Edge& e) const {  // 用于排序的比较运算符
        return w < e.w;
    }
};

vector<Edge> edges;  // 存边
int parent[MAXN];  // 记录每个节点所在的集合

int find(int x) {  // 查找 x 所在的集合
    if (parent[x] != x) {
        parent[x] = find(parent[x]);
    }
    return parent[x];
}

int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int u, v, w;
        cin >> u >> v >> w;
        edges.push_back(Edge(u, v, w));  // 存储边
    }
    sort(edges.begin(), edges.end());  // 排序

    int cnt = 0;  // 记录已经选取的边数
    int ans = 0;  // 记录生成树的总权值

    for (int i = 1; i <= n; i++) {
        parent[i] = i;  // 初始化每个节点所在的集合
    }

    for (auto& e : edges) {  // 遍历所有边
        int u = e.u, v = e.v, w = e.w;
        int pu = find(u), pv = find(v);
        if (pu != pv) {  // 如果 u 和 v 不在同一个集合中
            parent[pu] = pv;  // 合并集合
            ans += w;  // 更新生成树的总权值
            cnt++;
            if (cnt == n - 1) break;  // 已经选取了 n - 1 条边，可以退出循环
        }
    }

    cout << ans << endl;  // 输出生成树的总权值

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

以上就是 Prim 算法和 Kruskal 算法的 C++ 代码实现及详解。

三、Java 实现最小生成树算法及代码详解

最小生成树算法是一个经典的图论问题，主要解决的是一个无向图中连接所有顶点的问题，但是连接的边的权值和必须达到最小。常见的最小生成树算法有 Prim 算法和 Kruskal 算法。本文将介绍如何使用 Java 语言实现 Prim 算法和 Kruskal 算法，以及代码详解。

1. Prim 算法实现

Prim 算法是一个贪心算法，它的基本思想是从一个顶点开始，不断地选择与当前已选定的顶点相连且具有最小边权值的顶点，直到所有顶点都被选定。具体实现步骤如下：

1. 将起点加入到集合中，标记为已访问。
2. 将起点到其它顶点的所有边加入到一个集合中，并按照边的权值从小到大排序。
3. 选择权值最小的边，将其与另一个顶点加入到集合中，并标记为已访问。
4. 重复步骤 2 和 3 直到所有的顶点都被访问。

下面是 Prim 算法的 Java 实现代码：

public class Prim {

    /**
     * 使用邻接矩阵表示图
     * @param graph
     * @param start
     * @return
     */
    public static List<Edge> prim(int[][] graph, int start) {
        int n = graph.length; // 图的节点个数
        boolean[] visited = new boolean[n]; // 用于记录每个节点是否被访问过
        List<Edge> edges = new ArrayList<>(); // 用于存储最小生成树的边

        // 将起点标记为已访问
        visited[start] = true;

        // 从起点开始，不断选择与当前已选定的顶点相连且具有最小边权值的顶点
        while (edges.size() < n - 1) {
            int minWeight = Integer.MAX_VALUE; // 记录当前最小边权值
            Edge minEdge = null; // 记录当前最小边
            for (int i = 0; i < n; i++) {
                if (visited[i]) {
                    for (int j = 0; j < n; j++) {
                        if (!visited[j] && graph[i][j] > 0 && graph[i][j] < minWeight) {
                            minWeight = graph[i][j];
                            minEdge = new Edge(i, j, minWeight);
                        }
                    }
                }
            }

            // 将当前最小边的另一个节点加入到集合中，并标记为已访问
            visited[minEdge.to] = true;
            edges.add(minEdge);
        }

        return edges;
    }

    /**
     * 表示一条边
     */
    static class Edge {
        int from;
        int to;
        int weight;

        public Edge(int from, int to, int weight) {
            this.from = from;
            this.to = to;
            this.weight = weight;
        }

        @Override
        public String toString() {
            return "(" + from + ", " + to + ", " + weight + ")";
        }
    }

    public static void main(String[] args) {
        int[][] graph = {
                {0, 7, 0, 5, 0, 0, 0},
                {7, 0, 8, 9, 7, 0, 0},
                {0, 8, 0, 0, 5, 0, 0},
                {5, 9, 0, 0, 15, 6, 0},
                {0, 7, 5, 15, 0, 8, 9},
                {0, 0, 0, 6, 8, 0, 11},
                {0, 0, 0, 0, 9, 11, 0}
        };

        List<Edge> edges = prim(graph, 0);
        for (Edge edge : edges) {
            System.out.println(edge);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

2. Kruskal 算法实现

Kruskal 算法也是一个贪心算法，它的基本思想是先将图中所有的边按照权值从小到大排序，然后依次选择每条边，将其加入到最小生成树中，直到所有的节点都被连接。具体实现步骤如下：

1. 将所有边按照权值从小到大排序。
2. 依次选择每条边，如果边的两个端点不在同一个连通分量中，则将其加入到最小生成树中。
3. 重复步骤 2 直到所有的节点都被连接。

下面是 Kruskal 算法的 Java 实现代码：

public class Kruskal {

    /**
     * 使用邻接矩阵表示图
     * @param graph
     * @return
     */
    public static List<Edge> kruskal(int[][] graph) {
        int n = graph.length; // 图的节点个数
        List<Edge> edges = new ArrayList<>(); // 用于存储最小生成树的边

        // 将所有边按照权值从小到大排序
        PriorityQueue<Edge> heap = new PriorityQueue<>(Comparator.comparingInt(e -> e.weight));
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (graph[i][j] > 0) {
                    heap.offer(new Edge(i, j, graph[i][j]));
                }
            }
        }

        // 初始化并查集
        int[] parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }

        // 依次选择每条边，如果边的两个端点不在同一个连通分量中，则将其加入到最小生成树中
        while (edges.size() < n - 1 && !heap.isEmpty()) {
            Edge edge = heap.poll();
            int from = edge.from;
            int to = edge.to;
            int weight = edge.weight;
            if (find(parent, from) != find(parent, to)) {
                union(parent, from, to);
                edges.add(edge);
            }
        }

        return edges;
    }

    /**
     * 查找节点所在的集合
     * @param parent
     * @param node
     * @return
     */
    private static int find(int[] parent, int node) {
        while (node != parent[node]) {
            parent[node] = parent[parent[node]];
            node = parent[node];
        }
        return node;
    }

    /**
     * 合并两个集合
     * @param parent
     * @param x
     * @param y
     */
    private static void union(int[] parent, int x, int y) {
        int rootX = find(parent, x);
        int rootY = find(parent, y);
        if (rootX != rootY) {
            parent[rootX] = rootY;
        }
    }

    /**
     * 表示一条边
     */
    static class Edge {
        int from;
        int to;
        int weight;

        public Edge(int from, int to, int weight) {
            this.from = from;
            this.to = to;
            this.weight = weight;
        }

        @Override
        public String toString() {
            return "(" + from + ", " + to + ", " + weight + ")";
        }
    }

    public static void main(String[] args) {
        int[][] graph = {
                {0, 7, 0, 5, 0, 0, 0},
                {7, 0, 8, 9, 7, 0, 0},
                {0, 8, 0, 0, 5, 0, 0},
                {5, 9, 0, 0, 15, 6, 0},
                {0, 7, 5, 15, 0, 8, 9},
                {0, 0, 0, 6, 8, 0, 11},
                {0, 0, 0, 0, 9, 11, 0}
        };

        List<Edge> edges = kruskal(graph);
        for (Edge edge : edges) {
            System.out.println(edge);
        }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105