热门标签
热门文章
- 1【jetson笔记】ubuntu设置代理解决访问github问题_jeston nano怎么打开网络代理
- 2ValueError: Input X contains NaN. SVC does not accept missing values encoded as NaN natively.完美解决办法
- 3第6章域控制器安全_{"dc":"bxza29"}
- 4MQ为什么比数据库快_mq 为什么快
- 5BigData之Spark:Spark(大数据通用的分布式开源计算引擎)的简介、下载、经典案例之详细攻略_dataspark
- 6Kafka主题topic和分区Partition介绍_查询kafka topic.create.defalut.partitions
- 7嵌入式毕设分享 - 基于STM32的智能路灯设计与实现 - 物联网 嵌入式 单片机_基于stm32智能路灯
- 8使用Kafka实现大规模分布式消息系统
- 9Hvv--知攻善防应急响应靶机--Linux2
- 10数学建模的32种常规方法及案例代码_穷举法数学建模
当前位置: article > 正文
第7周博客,并查集笔记
作者:空白诗007 | 2024-07-04 11:34:51
赞
踩
第7周博客,并查集笔记
目录
并查集 (Disjoint-set)
Step 1:
Step2:
Step 3:
Step 4:
避免最坏情况:
继续优化:
I - Namesolo 拜师
一:维护生成树
二:按秩合并
证明:
三:路径压缩
并查集 (Disjoint-set)
每个集合用一棵“有根树”表示 定义数组 set[1…n] set[i] = i, 则i表示本集合,且是集合对应树的根 set[i] = j,j<>i, 则 j 是 i 的父节点.
- int findSet(int x)
- {
- if (x == set[x])
- return x;
- else
- return findSet(set[x]);
- }
- void unionSet(int x, int y)
- {
- int fx = findSet(x);
- int fy = findSet(y);
- set[fy] = fx;
- }
Step 1: nobody is anybody friend. We have 5 trees and each tree has a single element, which is the root and the representative of that tree.
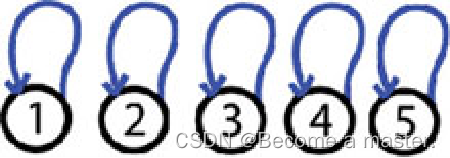
| i | 1 | 2 | 3 | 4 | 5 |
| set[i] | 1 | 2 | 3 | 4 | 5 |
Step2: 1 and 2 are friends, unionSet(1, 2) Then we have 4 trees one tree contain 2 elements and have the root 1. The other trees have a single element.
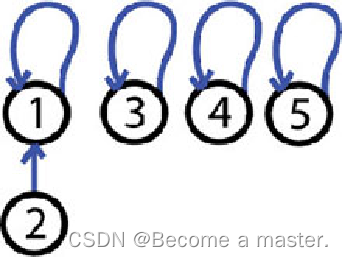
| i | 1 | 2 | 3 | 4 | 5 |
| set[i] | 1 | 1 | 3 | 4 | 5 |
Step 3: 5 and 4 are friends, unionSet(5, 4) Now we have 3 trees, 2 trees with 2 elements and one tree with one element.
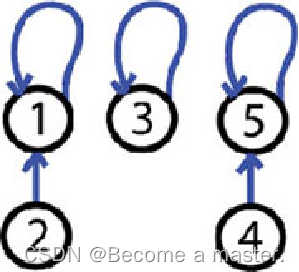
| i | 1 | 2 | 3 | 4 | 5 |
| set[i] | 1 | 1 | 3 | 5 | 5 |
Step 4: 5 and 1 are friends, unionSet(1, 5) Now we have 2 trees, one tree has 4 elements and the other one has only one element.
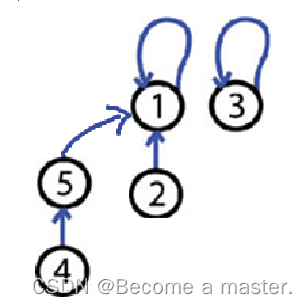
| i | 1 | 2 | 3 | 4 | 5 |
| set[i] | 1 | 1 | 3 | 5 | 1 |
算法复杂度: findSet(x) 最坏O(n) unionSet(x, y) 最坏O(n)
最坏:

避免最坏情况:
启发式合并 方法:将深度小的树合并到深度大的树 实现:假设两棵树的深度分别为h1和h2, 则合并后的树的高度h是: max(h1,h2), if h1<>h2. h1+1, if h1=h2. 效果:任意顺序的合并操作以后,包含k个节点的树的最大高度不超过lgk
- void unionSet(int x, int y)
- {
- fx = findset(x);
- fy = findset(y);
- if(rank[fx] > rank[fy])
- {
- set[fy] = fx;
- }
- else
- {
- set[fx] = fy;
- if(rank[fx] == rank[fy])
- rank[fy]++;
- }
- }
继续优化:
路径压缩(Path Compression) 思想:每次查找的时候,把经过路径上的点的父亲都设为根 步骤: 第一步,找到根结点 第二步,修改查找路径上的所有节点,将它们都指向根结点 可以证明m次操作的总时间复杂度为k*O(m),k是一个接近1的常数,即几乎是线性的。 使用路径压缩的并查集算法不需要再使用启发式合并。
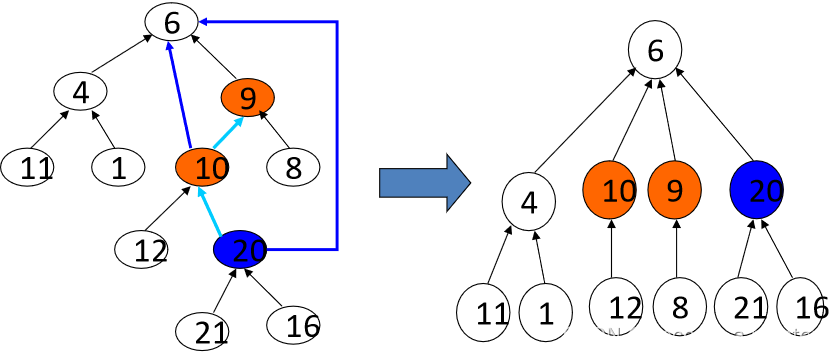
- int findSet(int x)
- {
- if (x == set[x])
- return x;
- else
- return set[x] = findSet(set[x]);
- }
I - Namesolo 拜师
给定
n
个点的图,初始没有边,要求支持以下操作:
•
加一条边
(
u
,
v
)
。
•
询问
u
,
v
是否连通。
并查集裸题,需要注意使用快读输入,以及取模输出。
一:维护生成树
只需要维护联通性,那么只要维护一棵生成树即可。
•
每次询问是否连通,只需要查是否在同一棵树内,一直向上询问直到得到树根是否相同即可。
•
加边前先判断是否连通,若不连通,将其中一个端点设为另 一端点的双亲节点。
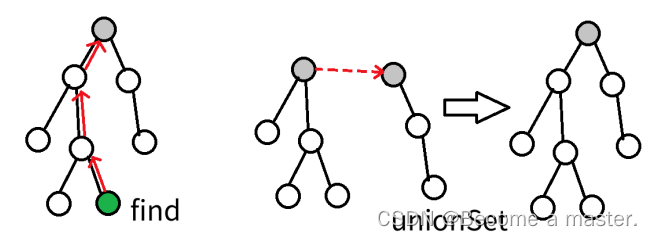
期望复杂度 O(m log n),最坏复杂度 O(nm)。
二:按秩合并
设节点
x
的秩
rank
x
表示以
x
为根子树树高(最深叶子到
x
的 距离),为减少树高,将秩小的节点的双亲节点设为秩大的节点。
•
两棵树树高不同时,最终树高等于树高较大的树的树高。
•
树高相同时,最终树高等于树高较大的树的树高
+1
。
设以
x
为根的子树节点个数为
n
,则其秩不超过
⌊
log
2
n
⌋
证明:
n
= 1
时,
rank
x
= 0 =
⌊
log
2
1
⌋
假设
n
= 1
,
2
, ...,
k
时均满足秩不超过
⌊
log
2
n
⌋
n
=
k
+ 1
时,设
u
,
v
所在的树大小分别为
a
,
b
,其中
a
≤
b
若
rank
u !
=
rank
v
,则
newrank
=
max
(
rank
u
,
rank
v
)
≤
max
(
⌊
log
2
a
⌋
,
⌊
log
2
b
⌋
)
≤ ⌊
log
2
n
⌋
若
rank
u
=
rank
v
,则
newrank
=
rank
u
+ 1
≤ ⌊
log
2
a
⌋
+ 1 =
⌊
log
2
2
a
⌋ ≤ ⌊
log
2
n
⌋
期望复杂度
O
(
m
log
n
)
,最坏复杂度
O
(
m
log
n
)
。
三:路径压缩
只需要寻找树根,重复询问同一个节点,向上询问的路径重复。 向上询问到树根形成一条路径,每次询问这条路径上的节点,都 一定会到达树根。 直接将父亲节点修改为树根,减少重复路径访问。
期望复杂度 O(mα(n)),最坏复杂度 O(m log1+ m/n n)。
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/空白诗007/article/detail/786651
推荐阅读
相关标签


