SVM转化为对偶问题求解的原因_在 svm 中,引入拉格朗日乘子的主要作用是将原始的高维二次规划问题转化为其对偶

作者：空白诗007 | 2024-06-20 16:24:31

踩

在 svm 中,引入拉格朗日乘子的主要作用是将原始的高维二次规划问题转化为其对偶

我们使用拉格朗日乘子法可以将原问题转化为对偶问题：
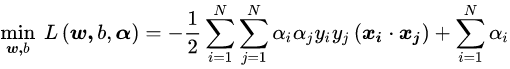
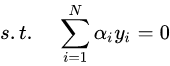
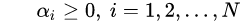
在这里插入图片描述

一、方便核函数的引入

在对偶问题中，需要计算內积 $x_i,x_j>$ 。在线性不可分的情况下，我们需要将特征映射到高维特征空间中，使其转化为高维空间线性可分问题。在高维特征空间计算內积是非常困难的，因此可以引用核函数，将高维特征空间的內积用低维空间的核函数表示：
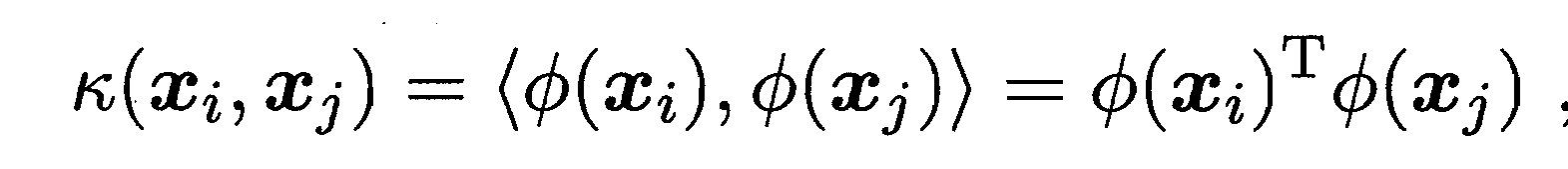
在这里插入图片描述

二、降低计算复杂度

原问题的求解复杂度与特征的维数相关，而转成对偶问题后只与问题的变量个数有关。
KKT条件：
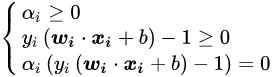
在这里插入图片描述
根据KKT条件，我们知道当 $\alpha_i >0$ 时，拉格朗日乘子所对应的变量为支持向量，其他变量的拉格朗日乘子为0，因此对偶问题计算时只与支持向量的个数有关，大大降低了计算复杂度。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/空白诗007/article/detail/740363

SVM转化为对偶问题求解的原因_在 svm 中,引入拉格朗日乘子的主要作用是将原始的高维二次规划问题转化为其 对偶

一、方便核函数的引入

二、降低计算复杂度

SVM转化为对偶问题求解的原因_在 svm 中,引入拉格朗日乘子的主要作用是将原始的高维二次规划问题转化为其对偶