五大经典算法之回溯法及其应用_回溯法属于经典法吗

前言

    回溯法是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”， 这就是回溯法的定义；这个和穷举法有些关联，都在不断的试探；而下面从从九宫格、八皇后、数独问题、来理解回溯法

回溯法的应用

九宫格问题

   我们要将4或者9个数或者16个数 n的n次方个数放入九宫格中，使得所有斜线和直线的数相加都等于相同的值，怎么解决这个问题；这就是通过回溯法可以解决的问题

解决问题的方法

• 现在第一行的中间填第一个数1
• 开始往右上角放数字，只要超过了上边，就放到下面，如果超过了左边就放右边

• 当遇到右上角有数据，这里就是回溯了，放到当前数据的下面，然后继续往右上走

•  就这样不断的往右上走，我们就能成下面的数独了

 代码实现

我们首先定义创建九宫格

public static int n=5;
    public static int[][] array=new int[n][n];

主要逻辑

首先定义填入的数据，和定义起始位置

 int x=1;//要填入的数据
        //定义起始位置
        int row=0;
        int col=n/2;
        array[row][col]=1;

 数组的行和列的位置开始填写后面的数据

 //开始填写后面的数据
        while(x<n*n){
            //在选择下一位置的时候，先记录下现在的位置
            int tempRow=row;
            int tempCol=col;
            //向右上移动
            row--;
            if(row<0){
                row=n-1;
            }
            col++;
            if(col==n){
                col=0;
            }
            x++;
            if(array[row][col]==0){//如果右上没填，直接填入
                array[row][col]=x;
            }else{//如果没填，就放到当前位置的下面
                //还原
                row=tempRow;
                col=tempCol;
                row++;
                array[row][col]=x;
            }
        }

• //在选择下一位置的时候，先记录下现在的位置int tempRow=row; int tempCol=col;
• row--;就是往右上走，如果row<0 则 放到最下面 row=n-1;
• col++; 如果col==n时 列号达到最大时， col=0； 
•  if(array[row][col]==0){//如果右上没填，直接填入； 直接填入
• 如果没填，就放到当前位置的下面 ；这里就涉及到还原  记录的 tempRow  进行还原

完整的代码

 
    public static int n=5;
    public static int[][] array=new int[n][n];
    //逻辑
    public static void squaredUp(int[][] array){
        int x=1;//要填入的数据
        //定义起始位置
        int row=0;
        int col=n/2;
        array[row][col]=1;
        //开始填写后面的数据
        while(x<n*n){
            //在选择下一位置的时候，先记录下现在的位置
            int tempRow=row;
            int tempCol=col;
            //向右上移动
            row--;
            if(row<0){
                row=n-1;
            }
            col++;
            if(col==n){
                col=0;
            }
            x++;
            if(array[row][col]==0){//如果右上没填，直接填入
                array[row][col]=x;
            }else{//如果没填，就放到当前位置的下面
                //还原
                row=tempRow;
                col=tempCol;
                row++;
                array[row][col]=x;
            }
        }
 
    }

八皇后问题

也就是在国际象棋中，放一个棋子上，而这个棋子斜线和直线 上都可以吃棋子，因此在摆放时，棋盘上放一个皇后，而这个皇后相互之间不能吃，这就是八皇后问题

 先放一个棋子，然后放第二个棋子时，就要判定和其他棋子是否能吃到，在周围试探放如果行就放，不行就退回上一行，从上一行找能放的格子，到最后八行都能放下去的时候就是八皇后了

• 也就是开始放到这里时 还可以

• 然后我们继续往下试

当遇到下面的情况，我们无法摆，就要退回去，重新找另外种方式摆，直到摆满8个就算解决问题了，这就是回溯法

 代码实现

设计思想，通过一维数组来表示二维数组，也就是  一维数组 ，用值表示哪个位置

 

 

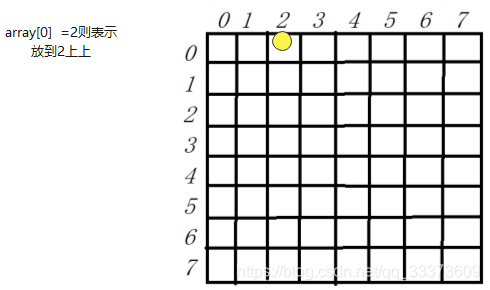
  //下标表示行号    值表示列号
    public static int[] array=new int[8];

• 然后处理8皇后的问题，首先考虑一个事情，要存放新的棋子时，我们要找到新的棋子与老的棋子不相交。也就是下面的图

 

•  需要专门判断当前列放入的位置和以前放入位置有冲突 从0开始，判断是否有冲突

 for(int i=0;i<n;i++){
            //条件1  array[i]==array[n]  在一列上
            //条件2  abs(n-i)==abs(array[n]-array[i])
            if(array[i]==array[n] || Math.abs(n-i)==Math.abs(array[n]-array[i])){
                return false;
            }
        }
        return true;

这里 在同一列很简单，也就是array[n]=array[i]则表明有冲突了，array[n] 表示当前要填的固定的比如是上面的4 固定的，而array[i]表示 之前填的位置，看是否相等的，就是刚才已经确定的 ，这里就没填。

•  怎么理解次对角线上的冲突拉，也就是

 

•  n-i绝对值等于array[n]-array[i] 的绝对值，这就是相同的，就在对角线上的

   最后

 //如果有结果了就退出
        if(row==8){
            printResult();
            System.out.println("---------");
            return;
        }
 
        //开始从第一列到最后一列一个个放入
        for(int col=0;col<8;col++){
            array[row]=col;
            if(judge(row)){//判断是否可以放入
                eightQueens(row+1);//就开始下一行
            }
        }

回溯是通过递归来做的，这就是解决8皇后问题

数独问题

规则

在9x9的方格上面，要求每一行和每一列从1到9的位置不重复的，然后每一个3x3的格子的数字，也是填1到9不能重复

• 我们开始从第一个开始填写，看是否满足 ，能满足就继续往前填，不能满足就退回来重新填

      这个和8皇后很像

 这里放4就有问题，然后就要重新在返回写过

代码实现

我们先写一个随意的二维数组，占好位

 public static int[][] result=new int[9][9];

• 判断数字是否可以用

 //判断行和列不重复
        for (int i = 0; i < 9; i++) {
            if(result[row][i]==number || result[i][col]==number){
                return false;
            }
        }

然后继续考虑3*3宫里面没有重复值

 要求到其中一个没有重复值，我们只要 行列位置除以三就行

 //判断自已所在的宫里面没有重复值
        int tempRow=row/3;
        int tempCol=col/3;
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                if(result[tempRow*3+i][tempCol*3+j]==number){
                    return false;
                }
            }
        }

进行判断就行 是否有重复值就行

• 我们从第一个开始往后填

public static void sudoku(){
        sudoku(0,0);
    }
    public static void sudoku(int i,int j){
        if(i==8 && j==9){
            printResult();
            return;
        }
        if(j==9){//横着放的时候，如果到了最右边，就回到下一行的第一个
            i++;
            j=0;
        }
        if(result[i][j]==0){//如果是空格
            for (int k = 1; k <= 9; k++) {
                if(judge(i,j,k)){
                    result[i][j]=k;
                    sudoku(i,j+1);
                    //让前一次的格子还原
                    result[i][j]=0;
                }
            }
        }else{
            sudoku(i,j+1);
        }
    }

这里不断往后放的时候，我们得还原空格，得还原回来。也就是等于0，就是递归下去。

这有很多组解得。

总结

最后学习回溯法，和递归关系比较密切，穷举法，效率大家能想到比较低，我们是为了解决某些问题用回溯法，也算是我们常用经典得算法。