二叉搜索树_二叉搜索树查找

作者：神奇cpp | 2024-07-03 13:49:37

踩

二叉搜索树查找

二叉搜索树

1.二叉搜索树概念
2.二叉树的操作
3.二叉搜索树的实现

1.二叉搜索树概念

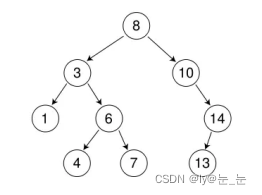
二插搜索树，也称为二叉查找树（BST），是一种特殊的二叉树，它的每个节点都包含一个可进行比较的键及其对应的值，且每个节点的左子树中所有键都小于该节点的键，右子树中所有键都大于该节点的键。
二叉搜索树是一种递归数据结构，它或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不为空，则左子树上所有节点的值都小于它的根节点；若它的右子树不为空，则右子树上所有节点的值都大于它的根节点；它的左右子树也分别为二叉搜索树。
在这里插入图片描述

2.二叉树的操作

二叉搜索树的查找
a、从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。
b、最多查找高度次，走到到空，还没找到，这个值不存在。
二叉搜索树的插入
插入的具体过程如下：
a. 树为空，则直接新增节点，赋值给root指针
b. 树不空，按二叉搜索树性质查找插入位置，插入新节点。
二叉搜索树的删除（主要d情况）
首先查找元素是否在二叉搜索树中，如果不存在，则返回, 否则要删除的结点可能分下面四种情况：
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
其中情况a可以与情况b或者c合并起来，所以真正的删除过程如下：
情况b：删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点–直接删除
情况c：删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点–直接删除
情况d：这种情况用替换法删除较为简单，在它的右子树中寻找最小结点，（或者左子树最大节点）用它的值填补到被删除节点中，最后删除该节点即可–替换法删除

3.二叉搜索树的实现

首先我们需要一个结点，且这个结点类数据的类型用模版来实现较好；

	template<class K>
	struct BSTreeNode
	{
		BSTreeNode<K>* _left;
		BSTreeNode<K>* _right;
		K _key;

		BSTreeNode(const K& key)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
		{}
	};
1
2
3
4
5
6
7
8
9
10
11
12
13

然后构建一个二叉搜索树的类，如下：

class BSTree
{
	typedef BSTreeNode<K> Node;//typedef一下，方便书写
public:
	//构造函数
	BSTree()
		:_root(nullptr)
		{}
	//析构函数
	~BSTree()
	{
		Destroy(_root);
	}
protected://不希望在类外面掉调到的函数用protected保护起来
	void Destroy(Node*& root)
	{
		if (root == nullptr)
			return;

		Destroy(root->_left);
		Destroy(root->_right);

		delete root;
		root = nullptr;
	}
private：
	Node* _root;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

插入数据：若树为空，则直接新增节点，赋值给root指针；若树不为空，比树的值大，在树的右边寻找，比树的值小，在树的左边寻找；找到位置后，需要将插入数据和树连接起来，所以还需要该节点的父节点，最后在判断要插入父节点的左边还是右边；
非递归：

	bool Insert(const K& key)
	{
		if (_root == NULL)
		{
				_root = new Node(key);
				return true;
			}
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else
				{
					return false;
				}
			}
			cur = new Node(key);
			//插入父节点的左边还是右边
			if (parent->_key > key)
			{
				parent->_left = cur;
			}
			else
			{
				parent->_right = cur;
			}
			return true;
		}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

递归：
递归一般要在类里面套一层，因为递归调位需要传参（_root），而在类外不能访问_root;bool _InsertR(Node*& root, const K& key)，要引用root，这样就容易连接起来；

		bool InsertR(const K& key)
		{
			return _InsertR(_root, key);
		}
	protected:
		bool _InsertR(Node*& root, const K& key)
		{
			if (root == NULL)
			{
				root = new Node(key);
				return true;
			}
			if (root->_key > key)
			{
				return _InsertR(root->_left, key);
			}
			else if (root->_key < key)
			{
				return _InsertR(root->_right, key);
			}
			else
			{
				return false;
			}
		} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

查找：查找较简单，比树的值大，在树的右边寻找，比树的值小，在树的左边寻找；
非递归：

		bool Find(const K& key)
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else
				{
					return true;
				}
			}
			return false;
		}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

递归：

		bool FindR(const K& key)
		{
			return _FindR(_root, key);
		}
	protected:
		bool _FindR(Node* root, const K& key)
		{
			if (root == nullptr)
				return false;
			if (root->_key == key)
				return true;
			if (root->_key > key)
			{
				return _FindR(root->_left, key);
			}
			else
			{
				return _FindR(root->_right, key);
			}
		}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

删除：
情况b：删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点–直接删除
情况c：删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点–直接删除
情况d：这种情况用替换法删除较为简单，在它的右子树中寻找最小结点，（或者左子树最大节点）用它的值填补到被删除节点中，最后删除该节点即可–替换法删除
非递归：

bool Erase(const K& key)
		{
			Node* parent = _root;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else
				{
					//左为空
					if (cur->_left == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_right;
						}
						else
						{
							if (parent->_left == cur)
							{
								parent->_left = cur->_right;
							}
							else
							{
								parent->_right = cur->_right;
							}
						}
						delete cur;
					}
					//右为空
					else if (cur->_right == nullptr)
					{
						if (cur == _root)
						{
							_root == cur->_left;
						}
						else
						{
							if (parent->_left == cur)
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;
							}
						}
						delete cur;
					}
					//都不为空,
					else
					{
						// 找右树最小节点替代，
						//Node* pminRight = cur;
						//Node* minRight = cur->_right;
						//while (minRight->_left)
						//{
						//	pminRight = minRight;
						//	minRight = minRight->_left;
						//}
						//cur->_key = minRight->_key;
						//if (pminRight->_left == minRight)
						//{
						//	pminRight->_left = minRight->_right;
						//}
						//else
						//{
						//	pminRight->_right = minRight->_right;
						//}
						//delete minRight;
						
						//可以是左树最大节点替代
						Node* pmaxLeft = cur;
						Node* maxLeft = cur->_left;
						while (maxLeft->_right)
						{
							pmaxLeft = maxLeft;
							maxLeft = maxLeft->_right;
						}
						cur->_key = maxLeft->_key;
						if (pmaxLeft->_left == maxLeft)
						{
							pmaxLeft->_left = maxLeft->_left;
						}
						else
						{
							pmaxLeft->_right = maxLeft->_left;
						}
						delete maxLeft;
					}
					return true;
				}
			}
			return false;
		}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104

递归：

		bool EraseR(const K& key)
		{
			return _EraseR(_root, key);
		}
	protected:
		bool _EraseR(Node*& root, const K& key)
		{
			if (root == nullptr)
				return false;
			if (root->_key > key)
			{
				return _EraseR(root->_left, key);
			}
			else if (root->_key < key)
			{
				return _EraseR(root->_right, key);
			}
			else
			{
				Node* cur = root;
				if (root->_left == nullptr)
				{
					root = root->_right;
				}
				else if (root->_right == nullptr)
				{
					root = root->_left;
				}
				else
				{
					Node* maxLeft = root->_left;
					while (maxLeft->_right)
					{
						maxLeft = maxLeft->_right;
					}
					swap(cur->_key, maxLeft->_key);
					return _EraseR(root->_left, key);
				}
				delete cur;
				return true;
			}
		}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

完整代码如下：

	//结点
	template<class K>
	struct BSTreeNode
	{
		BSTreeNode<K>* _left;
		BSTreeNode<K>* _right;
		K _key;

		BSTreeNode(const K& key)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
		{}
	};
	template<class K>
	class BSTree
	{
		typedef BSTreeNode<K> Node;
	public:
		BSTree()
			:_root(nullptr)
			{}
		//BSTree() = default;//制定强制生成默认构造参数
		void InOrder()
		{
			_InOrder(_root);
			cout << endl;
		}
		~BSTree()
		{
			Destroy(_root);
		}
		bool Insert(const K& key)
		{
			if (_root == NULL)
			{
				_root = new Node(key);
				return true;
			}
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else
				{
					return false;
				}
			}
			cur = new Node(key);
			if (parent->_key > key)
			{
				parent->_left = cur;
			}
			else
			{
				parent->_right = cur;
			}
			return true;
		}
		bool Find(const K& key)
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else
				{
					return true;
				}
			}
			return false;
		}
		bool Erase(const K& key)
		{
			Node* parent = _root;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else
				{
					//左为空
					if (cur->_left == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_right;
						}
						else
						{
							if (parent->_left == cur)
							{
								parent->_left = cur->_right;
							}
							else
							{
								parent->_right = cur->_right;
							}
						}
						delete cur;
					}
					//右为空
					else if (cur->_right == nullptr)
					{
						if (cur == _root)
						{
							_root == cur->_left;
						}
						else
						{
							if (parent->_left == cur)
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;
							}
						}
						delete cur;
					}
					//都不为空,
					else
					{
						// 找右树最小节点替代，
						//Node* pminRight = cur;
						//Node* minRight = cur->_right;
						//while (minRight->_left)
						//{
						//	pminRight = minRight;
						//	minRight = minRight->_left;
						//}
						//cur->_key = minRight->_key;
						//if (pminRight->_left == minRight)
						//{
						//	pminRight->_left = minRight->_right;
						//}
						//else
						//{
						//	pminRight->_right = minRight->_right;
						//}
						//delete minRight;
						
						//可以是左树最大节点替代
						Node* pmaxLeft = cur;
						Node* maxLeft = cur->_left;
						while (maxLeft->_right)
						{
							pmaxLeft = maxLeft;
							maxLeft = maxLeft->_right;
						}
						cur->_key = maxLeft->_key;
						if (pmaxLeft->_left == maxLeft)
						{
							pmaxLeft->_left = maxLeft->_left;
						}
						else
						{
							pmaxLeft->_right = maxLeft->_left;
						}
						delete maxLeft;
					}
					return true;
				}
			}
			return false;
		}
		bool FindR(const K& key)
		{
			return _FindR(_root, key);
		}
		bool InsertR(const K& key)
		{
			return _InsertR(_root, key);
		}
		bool EraseR(const K& key)
		{
			return _EraseR(_root, key);
		}
	protected:
		bool _FindR(Node* root, const K& key)
		{
			if (root == nullptr)
				return false;
			if (root->_key == key)
				return true;
			if (root->_key > key)
			{
				return _FindR(root->_left, key);
			}
			else
			{
				return _FindR(root->_right, key);
			}
		}
		bool _InsertR(Node*& root, const K& key)
		{
			if (root == NULL)
			{
				root = new Node(key);
				return true;
			}
			if (root->_key > key)
			{
				return _InsertR(root->_left, key);
			}
			else if (root->_key < key)
			{
				return _InsertR(root->_right, key);
			}
			else
			{
				return false;
			}
		} 
		bool _EraseR(Node*& root, const K& key)
		{
			if (root == nullptr)
				return false;
			if (root->_key > key)
			{
				return _EraseR(root->_left, key);
			}
			else if (root->_key < key)
			{
				return _EraseR(root->_right, key);
			}
			else
			{
				Node* cur = root;
				if (root->_left == nullptr)
				{
					root = root->_right;
				}
				else if (root->_right == nullptr)
				{
					root = root->_left;
				}
				else
				{
					Node* maxLeft = root->_left;
					while (maxLeft->_right)
					{
						maxLeft = maxLeft->_right;
					}
					swap(cur->_key, maxLeft->_key);
					return _EraseR(root->_left, key);
				}
				delete cur;
				return true;
			}
		}
		void Destroy(Node*& root)
		{
			if (root == nullptr)
				return;

			Destroy(root->_left);
			Destroy(root->_right);

			delete root;
			root = nullptr;
		}
		void _InOrder(Node* root)
		{
			if (root == nullptr)
				return;

			_InOrder(root->_left);
			cout << root->_key << " ";
			_InOrder(root->_right);
		}
	private:
		Node* _root = nullptr;
	};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/神奇cpp/article/detail/783353