Unity3D C#数学系列之点积_设 向量a(a,b,c) 和 向量b(e,f,g); 那么求在c#里面计算 他们的外积和点积的 代码

---

1 定义

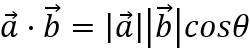
可知，点积得到的是一个标量，这个标量代表什么呢？

2 几何意义

如果$\vec{b}$为单位向量，则表示向量$\vec{a}$在向量$\vec{b}$上的投影长度。

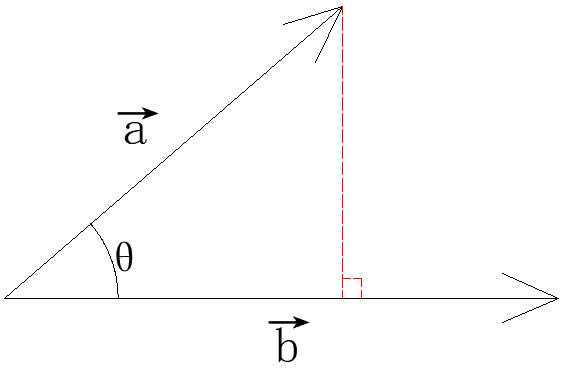
3 向量a·向量b = x_ax_b+y_ay_b+z_az_b

上面这公式是怎么来的？
设

根据余弦定理有

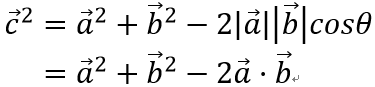
所以

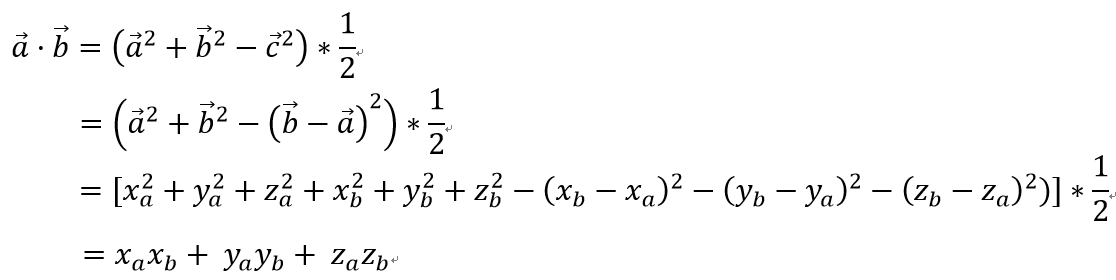
4 应用案例

4.1 求两向量的夹角

已知向量

根据点积的定义，则有

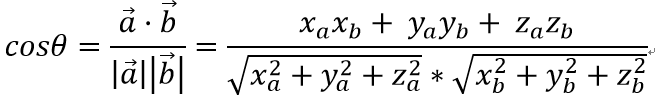
当然，这个方法Unity已经帮我封装好了，咱们要求两个向量的夹角，直接用Vector3.Angle这个方法就好。Vector3.Angle的源码如下，可以看到其内部其实就是实现了上面这个公式。

    /// <summary>
    ///   <para>Returns the angle in degrees between from and to.</para>
    /// </summary>
    /// <param name="from">The vector from which the angular difference is measured.</param>
    /// <param name="to">The vector to which the angular difference is measured.</param>
    /// <returns>
    ///   <para>The angle in degrees between the two vectors.</para>
    /// </returns>
    public static float Angle(Vector3 from, Vector3 to)
    {
      float num = (float) Math.Sqrt((double) from.sqrMagnitude * (double) to.sqrMagnitude);
      if ((double) num < 1.00000000362749E-15)
        return 0.0f;
      return (float) Math.Acos((double) Mathf.Clamp(Vector3.Dot(from, to) / num, -1f, 1f)) * 57.29578f;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

4.2 判断两向量是否垂直

两向量垂直时，两者夹角为90°，而cos90° = 0，故$\vec{a}$·$\vec{b}$ =0。
换句话说，只要$\vec{a}$和$\vec{b}$均不为空向量，只要$\vec{a}$·$\vec{b}$ =0，就说明两向量垂直。

4.3 判断NPC是否在攻击范围内

假设玩家的攻击范围为左右各60°，最大攻击半径为10。设玩家的位置为A(x_a , y_a, z_a)，怪兽的位置为B(x_b, y_b, z_b)，判断怪兽是否在人的攻击范围内？
很简单，先判断两者的距离是否小于10，若大于则不在攻击范围内。
再判断$\overrightarrow{AB}$与玩家前方的夹角是否小于30°，若大于则不在攻击范围内，若小于等于则在攻击范围内。
代码也很简单，两者的距离可通过Vector3.Distance求得，$\overrightarrow{AB}$与玩家前方的夹角通过Vector3.Angle求得，代码如下。

// 判断targetPos是否在视线范围内
public bool IsInView(Vector3 targetPos)
{
    // 玩家位置
    Vector3 selfPos = m_GameObject.transform.position;

    if (Vector3.Distance(selfPos, targetPos) > 10f)
        return false;

    Vector3 loorDir = targetPos - selfPos;
    if (Vector3.Angle(loorDir, m_GameObject.transform.forward) < 30f)
        return true;

    return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

然后在Unity中测试一下。可以看到，咱们的分析是正确的。

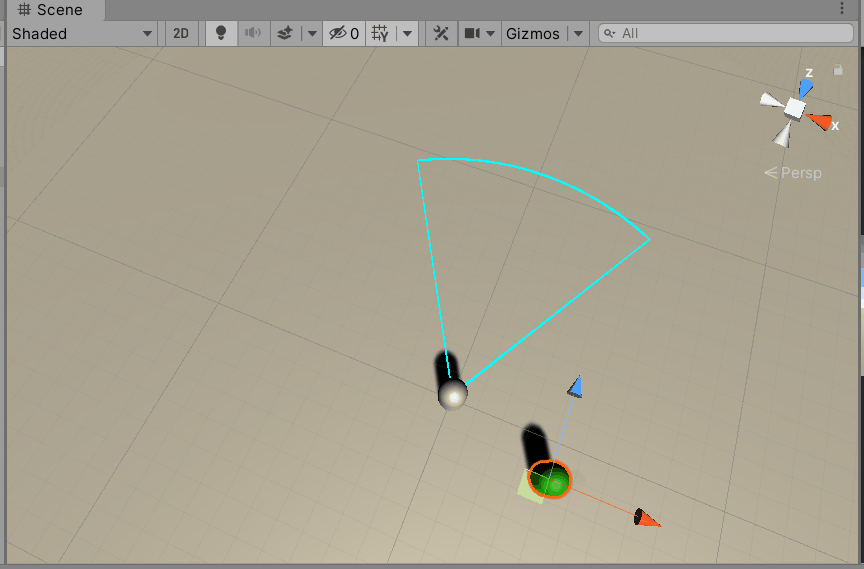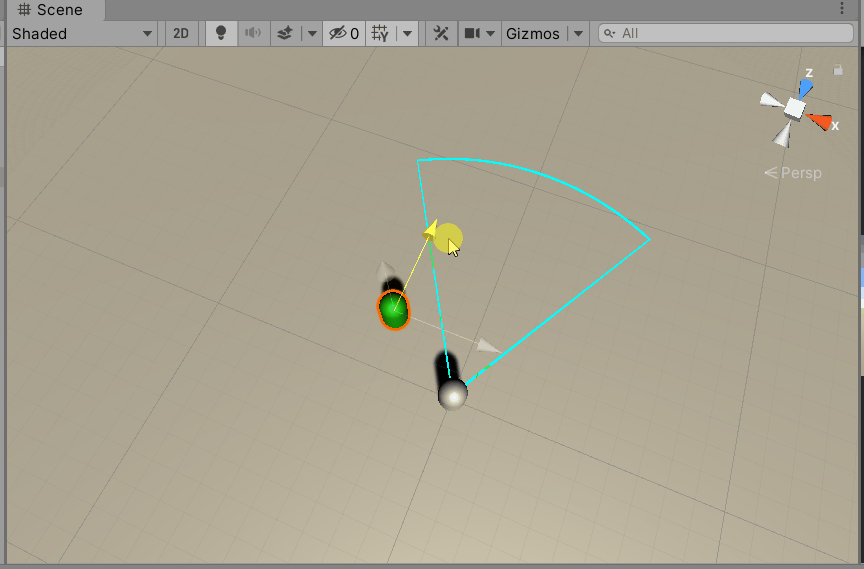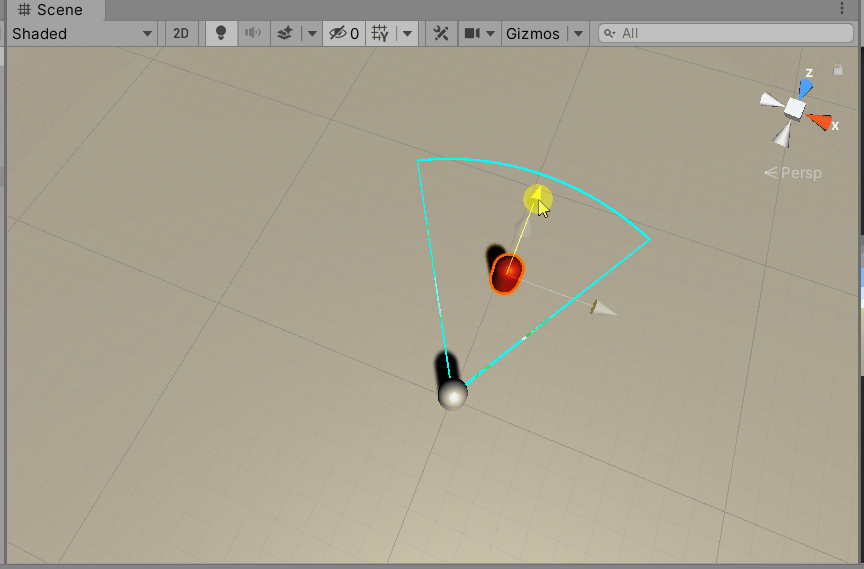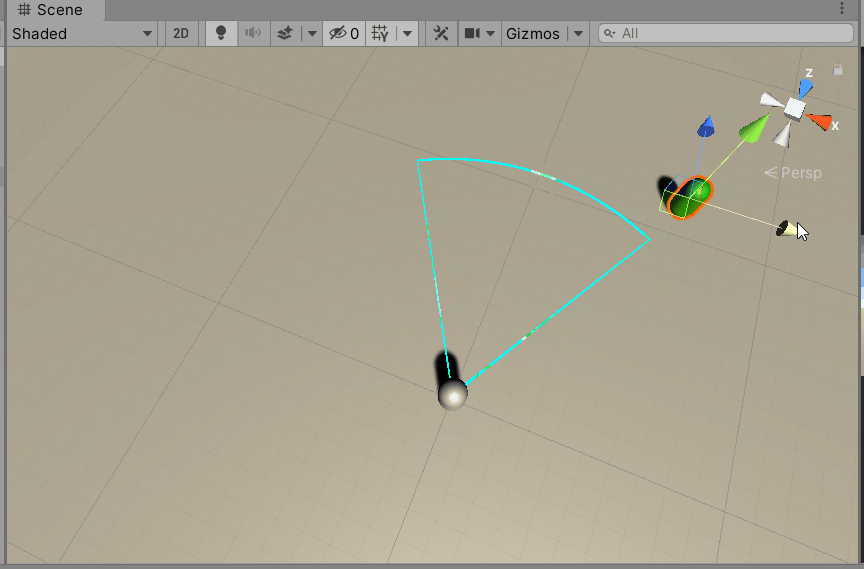
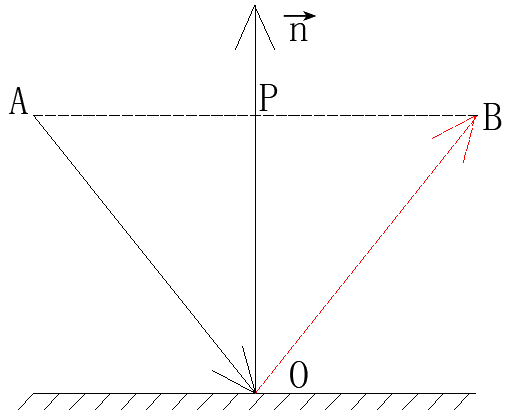
4.4 已知入射光线和表面法线求反射光线

如图，已知入射光线$\overrightarrow{AO}$和表面法线$\vec{n}$（假定为单位向量），求反射光线$\overrightarrow{OB}$。

直接看计算过程。

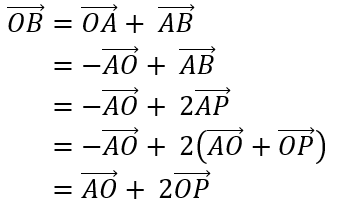
又

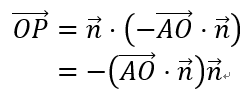
上面这公式怎么来的？还记得点积的几何意义吗？

如果$\vec{b}$为单位向量，则表示向量$\vec{a}$在向量$\vec{b}$上的投影长度。

这里的$\overrightarrow{OP}$的长度不正好是$\overrightarrow{OA}$在单位向量$\vec{n}$上的投影长度么。$\overrightarrow{OP}$的长度求到后，再乘以它的方向$\vec{n}$，咱们就求到$\overrightarrow{OP}$了。
完整的推导如下。

代码如下：

/// <summary>
/// 计算反射光线
/// </summary>
/// <param name="lightDir">入射光线</param>
/// <param name="normalDir">表面法线(单位向量)</param>
/// <returns>反射光线</returns>
private Vector3 CalcReflectDir(Vector3 lightDir, Vector3 normalDir)
{
    return lightDir - 2 * Vector3.Dot(lightDir, normalDir) * normalDir;
}
1
2
3
4
5
6
7
8
9
10

在Unity中验证一下。

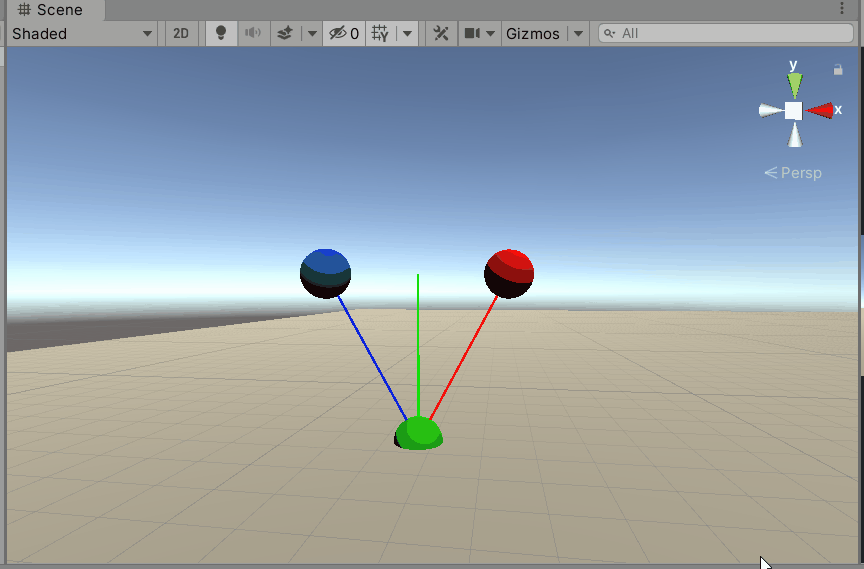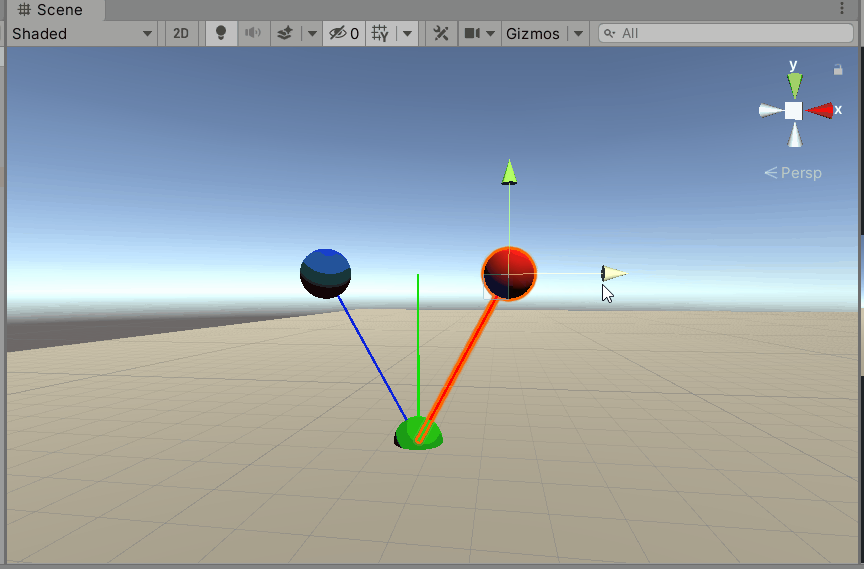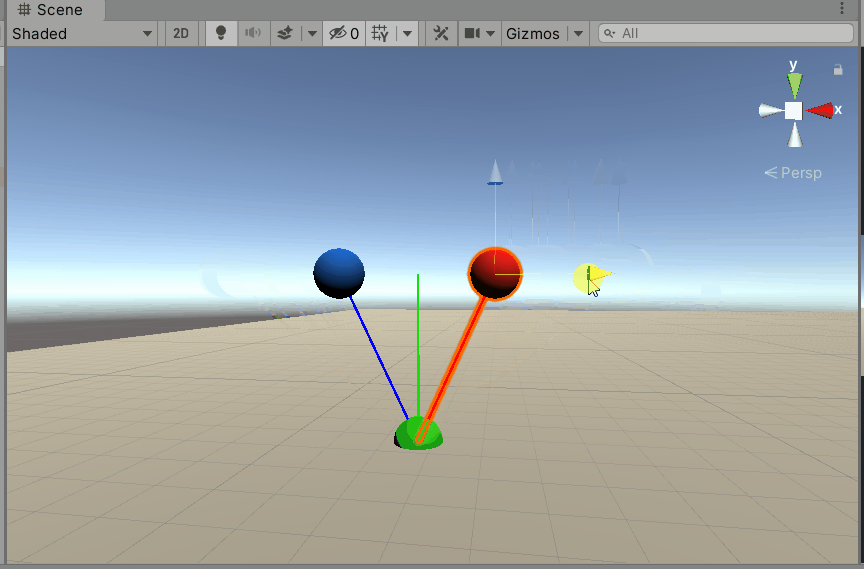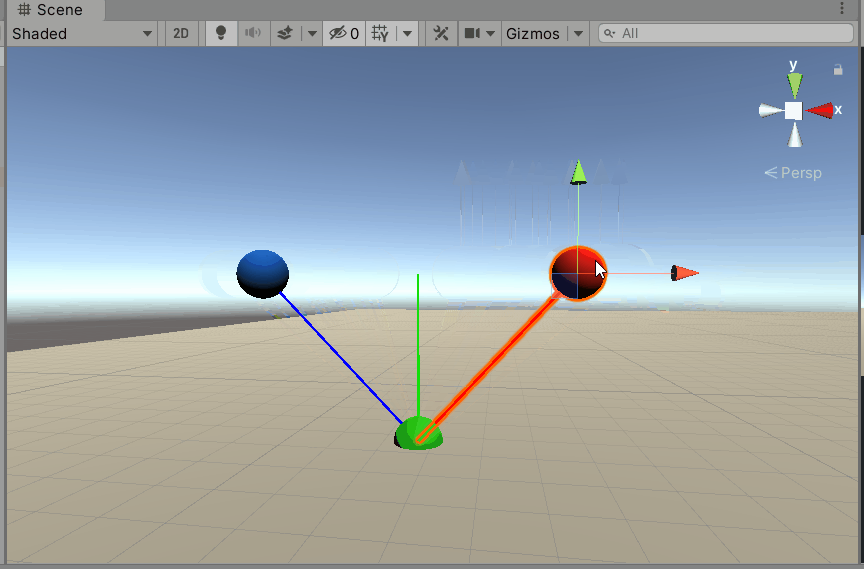
5 项目

链接：https://pan.baidu.com/s/1Sv7CCrnh88MEvB6evW-rQg
提取码：t4ix
博主本文博客链接。