算法——模拟专题(一篇搞定)_算法 模拟算法题

在本专栏已经更新双指针算法,滑动窗口算法,二分查找算法,前缀和算法以及位运算算法,欢迎大家跳转至相关专题阅读

此篇文章为大家带来算法专栏的模拟专题

模拟算法本质就是比葫芦画瓢，思路比较简单，就是将演算流程转化为代码

目录

1.替换所有的问号

1.1解析

1.2题解

2.提莫攻击

2.1解析

2.2题解

3.N字形变化

3.1解析

3.2题解

4.外观数组

4.1题解

4.2题解

5.数青蛙

5.1解析

优化

5.2题解

谢谢您的访问!!期待您的关注!!

---

---

1.替换所有的问号

题目：. - 力扣（LeetCode）

1.1解析

本质上就是将字符串里面的所有 ？ 字符 替换成任何一个a ~ z的字符，但是要，满足替换后的字符与该字符前一个字符和后一个字符不能相等

那么我们直接简单遍历后判断即可

但是要注意边界条件，第一个字符只能判断后一个字符，第二个字符只能判断前一个字符

1.2题解

class Solution {
     public String modifyString(String s) {
         char[] str = s.toCharArray();
         int n = str.length;
         for(int i = 0; i < n; i++){
             if(str[i] == '?'){
                 for(char ch = 'a'; ch <= 'z'; ch++){
                     if((i == 0 || ch != str[i-1]) && (i == n-1 || ch != str[i+1])){
                         str[i] = ch;
                         break;
                     }
                 }
             }
         }
         return String.valueOf(str);
     }
 }

---

2.提莫攻击

题目:. - 力扣（LeetCode）

2.1解析

题目给定一个数组,数组里面的元素代表英雄在第几秒接受攻击.那么英雄在接受攻击的时候如果是处于正常状态,那么就正常晕眩,此时总晕眩时间就加上duration即可; 但是如果再接受攻击的时候,上一个攻击的晕眩还没结束,那么就要重置晕眩,那么这段时间的晕眩时间就是 两个数组元素的时间差

因此,我们只需遍历数组,判断数组前一个元素和后一个元素只差是不是 >= duration,如果大于,那么 sum+= duration.小于的话就 sum += timeSeries[i+1] - timeSeries[i];

但是要注意:数组最后一个元素是没有后一个元素的,因此我们遍历完数组最后得到的结果要 + duration

2.2题解

 class Solution {
     public int findPoisonedDuration(int[] timeSeries, int duration) {
         int sum = 0;
         for(int i = 0; i < timeSeries.length-1; i++){
             sum += Math.min(timeSeries[i+1]-timeSeries[i],duration);
         }
         return sum + duration;
     }
 }

---

3.N字形变化

题目:. - 力扣（LeetCode）

3.1解析

遇到这种稍微复杂的题,我们可以试着找一下规律

如图所示,我们将字符串形成的下N字型时,各个位置下标都表明好来寻找规律

我们会发现,第一和最后一行,每两个元素之间的下标差是都是6;至于中间的行,我们可以成对看,即[1 5] [7 11],这样会发现,1 与 7 之间 和 5 与11 之间的差数也都是6;同理,[2 4] [8 10]也是一样的规律

因此我们只需要找出6这个数字的规律即可,题目的变量是n = 4,那么6 = 2 n - 2,是不是真的如此呢??

我们让n = 3,再次模拟,看看 差数 是不是 = 4即可

如图所示,那么我们两个下标之间的差数就是 2 n - 2

我们也不难发现,第一行的下标是从0开始的,以2n-2为公差的等差数列

第2行则两组等差数列,一组是从1开始,以2n-2为公差的等差数列,第二组就是从n - 1开始,以2

n-2为开始的等差数列

因此我们可以总结出下面这张图:

因此,我们横向遍历的时候,根据下标拿到对应的字符,再拼接即可

注意:如果n = 1的话,那么d就会 = 0,就会造成死循环,因此我们要处理边界情况

3.2题解

public static String convert(String s, int numRows) {
         if(numRows == 1){
             return s;
         }
         StringBuffer ret = new StringBuffer();
         int d = 2 * numRows - 2;
         char[] str = s.toCharArray();
         int n = str.length;
         //处理第一行
         for(int i = 0; i < n; i += d){
             ret.append(str[i]);
         }
 ​
         //处理中间行
         for(int i = 1; i < numRows-1; i++){
             for(int k = i,j = d-i; k < n || j < n; k += d,j += d){
                 if(k < n){
                     ret.append(str[k]);
                 }
                 if(j < n){
                     ret.append(str[j]);
                 }
             }
         }
 ​
         //处理最后一行
         for(int i = numRows-1; i < n; i += d){
             ret.append(str[i]);
         }
 ​
         return ret.toString();
     }

---

4.外观数组

题目:. - 力扣（LeetCode）

4.1题解

题目实际上就是要我们对一个字符串进行描述,如果这个字符串为 "1211",那么就是1个1,1个2,2个1,那么对他描述救是111221,对"111221"描述就是 "312211"

因此我们只需要遍历当前字符串,判断有几个相同连在一起的相同字符,用count记录,再拼接上字符串即可

对于记录的过程,我们可以利用双指针

fast一直往前走,直到遇到某个数不等于slow位置的值,那么count = fast - slow;接着slow = fast,再继续记录

4.2题解

class Solution {
     public String countAndSay(int num) {
         String ret = "1";
         for(int i = 1; i < num; i++){//只需要循环n-1次
             StringBuffer tmp = new StringBuffer();
             int slow = 0, fast = 0, n = ret.length();
             while(fast < n){
                 while(fast < n && ret.charAt(fast) == ret.charAt(slow)){
                     fast++;
                 }
                 tmp.append(Integer.toString(fast-slow));
                 tmp.append(ret.charAt(slow));
                 slow = fast;
             }
             ret = tmp.toString();
         }
         return ret;
     }
 }

---

5.数青蛙

题目:. - 力扣（LeetCode）

5.1解析

题目实际上就是给一个字符串,这个字符串是由若干个零散的"croak"组成的,而一个croak就是一个叫声,我们要判断要形成所给字符串,最少要几只青蛙

那么就会出现3种情况:

(1)类似"croakcroak"

是由若干个完整的croak组成的,那么一个青蛙叫完"croak"后,还可以继续叫第二个"croak",因此最少要1只青蛙

(2)类似"crcoakroak"

那么在第一只青蛙叫到"cr"后,又出现了c,因此是由2个零散的croak组成的,最少要2只

(3)类似"croakcrook"

会出现不是"croak"的组合,那么就不能被青蛙叫出来,直接返回-1

我们的核心就在于一只青蛙能否叫出一个完整的"croak"

我们可以利用哈希表来存当前这个"croak"的情况

如图所示,当我们判断的字符是c的时候,对应哈希表中的c的个数就要++,继续遍历

当我们继续遍历到'r'的时候,就要回头判断记录'c'字符是否大于0,即c字符是否被叫过,如果没有(为0),那么直接返回-1;如果有,那么说明此时青蛙叫到了'r'字符,那么'r'字符在哈希表中的数量就+1,而先前的'c'就-1;依次类推,当判断到'o'的时候就要回头看r是否被叫过.....,这样,但最后k = 1的时候,说明一个完整的"croak"被叫完了.

但是如上述例子,但我们遍历到第二个c的时候,实际上是可以由第一只青蛙继续叫的,因此我们在遍历到c字符的时候,就要判断此时哈希表中的'k'的数量是否>0.如果>0则要让这个'k'的数量-1,而'c'的数量+1,模拟重复叫的过程

当我们遍历完字符串后,哈续表中k的数量就是最少青蛙的个数,而此时其余的"croa"字符数量一定都是0,如果不是,说明有多余字符,那么返回-1

优化

如果我们直接按照上面的思路,在遇到'c'的时候判断'k',遇到'r'的时候判断'c'....,那么我们需要写5个if-else,

这道题是把"croak"当成一个已知条件,但是如果"croak"未知,或者这个字符串长度不止5,而是更长,那么我们就不能写那么多if-else

如果我们能把"croak"每个对应的位置关系记录下来就好了,像数组那样

我们可以利用哈希表来记录下"croak"每个字符对应的位置关系.

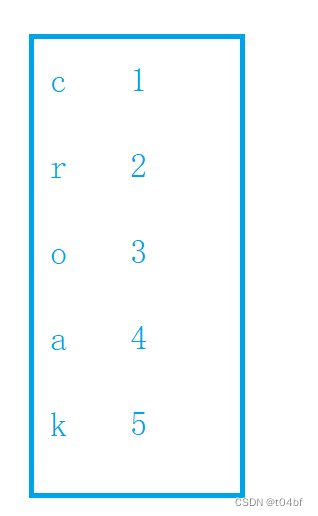
那么我们在遍历到每个字符的时候,就可以直接从哈希表中拿到这个字符的前一个字符进行判断了

5.2题解

 class Solution {
     public static int minNumberOfFrogs(String croakOfFrogs) {
         String t = "croak";
         int len = t.length();
         char[] str = croakOfFrogs.toCharArray();
         int[] hash = new int[len];
         Map<Character,Integer> index = new HashMap<>();
         for(int i = 0; i < len; i++){
             index.put(t.charAt(i),i);
         }
         for(char ch : str){
             if(ch == t.charAt(0)){
                 if(hash[len-1] != 0){
                     hash[len-1]--;
                 }
                 hash[0]++;
             }else{
                 int i = index.get(ch);
                 if(hash[i-1] == 0){
                     return -1;
                 }
                 hash[i-1]--;
                 hash[i]++;
             }
         }
         for(int i = 0; i < len-1; i++){
             if(hash[i] != 0){
                 return -1;
             }
         }
         return hash[len-1];
     }
 }

---

谢谢您的访问!!期待您的关注!!