使用Sklearn中线性回归（LinearRegression）模型与决策树回归（DecisionTreeRegressor）模型解决身高预测问题_多元线性回归与决策树

一、数据集height

1.1 数据集规格

身高数据集样本数量：共2700个样本

• 两个特征：足长、步幅（cm）
• 一个标签：身高（cm）

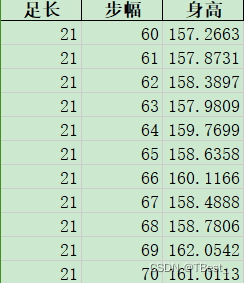
1.2 导入数据

利用pandas包，导入Excel文件，在命令行中安装pandas库：

pip install pandas

import pandas as pd
 
data = pd.read_excel("height.xlsx").values

二、数据预处理

2.1 获取数据并处理

        按照日常习惯，身高保留两位小数，顾在获取数据的时候，同时对身高进行保留两位小数的处理，但也可以不保留，保证数据训练出来的准确率。

import numpy as np
 
x_data = data[:, 0:2]  # 取数据集种的前两列
y_data = np.around(data[:, 2], 2)  # 身高保留两位小数

2.2 划分数据集

        划分训练集80%，测试集20%，随机种子12：

from sklearn.model_selection import train_test_split
 
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(
    x_data, y_data,
    test_size=0.2,
    random_state=12
)

三、建模分析

3.1 建立线性回归模型

3.1.1 线性回归

        线性回归(Linear Regression)是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法.

        线性回归利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模。 这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。

3.1.2 函数官方参数

1. fit_intercept: 是否计算截距项，默认为True。

2. normalize: 是否将数据正规化，默认为False。

3.1.3 代码

from sklearn.linear_model import LinearRegression
 
# 建立模型
model = LinearRegression()
model.fit(X_train, y_train)  # 使用训练集多模型进行训练

3.2 建立决策树回归模型

3.2.1 决策树

        什么是决策树，所谓决策树，就是一个类似于流程图的树形结构，树内部的每一个节点代表的是对一个特征的测试，树的分支代表该特征的每一个测试结果，而树的每一个叶子节点代表一个类别。树的最高层是就是根节点。下图即为一个决策树的示意描述，内部节点用矩形表示，叶子节点用椭圆表示。

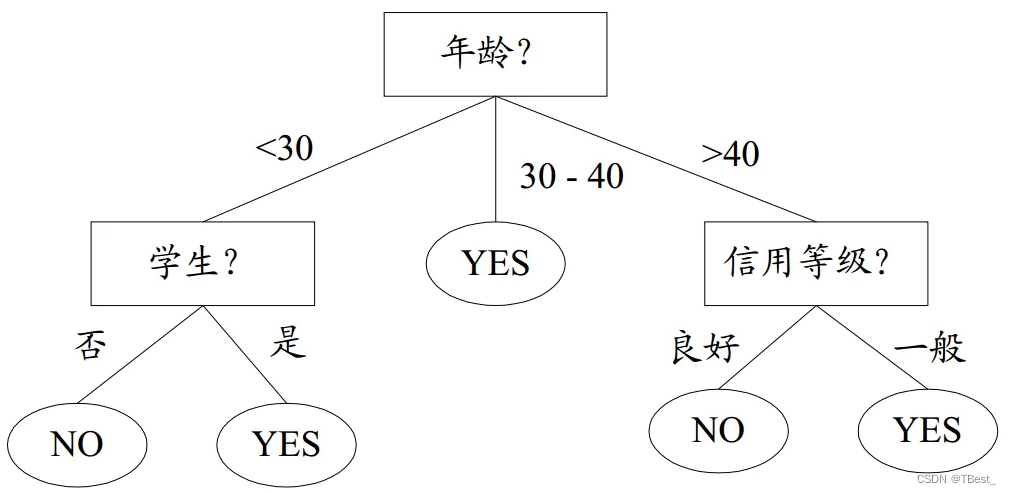
3.2.2 函数官方参数

class sklean.ree.DedisionTreeClassier(
criterione=gn ,pliter=tbest, 
max_depth=None, min_samples_sli=2, 
min samples_eaF-1, min_weight_fracion_JeaF=0.0,
 max_features=None, random_state=None, 
max_leaf_nodes=None min_inpurity_decrease=0.0,
min_impurity_split=None,
class_weight=None, presot=False)

以下是一些主要的参数：

criterion: 决定了决策树的分裂方式。可以选择"mse"（均方误差）或"mae"（平均绝对误差）。默认是"mse"。

splitter: 决定了在每个节点上进行特征的选择的算法。可以选择"best"或"random"。默认是"best"。

max_depth: 决策树的最大深度。默认是None，意味着除非树变得纯净，否则将会增长直到达到所有叶子都是纯净的状态。

min_samples_split: 节点在进一步划分所需的最小样本数。默认是2。

min_samples_leaf: 叶子节点中的最小样本数。默认是1。

max_features: 决策树构建过程中的最大特征数。默认是"auto"，意味着最大特征数是sqrt(n_features)。

random_state: 随机状态。设置之后，可以保证结果的可复现性。默认是None。

3.2.3 代码 

from sklearn.tree import DecisionTreeRegressor
 
model = DecisionTreeRegressor(max_depth=3)
model.fit(X_train, y_train)  # 训练模型

四、模型评估

4.1 评估指标

4.1.1 均方误差 (Mean Squared Error, MSE)

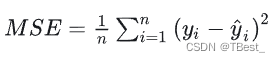
4.1.2 均方根误差 (Root Mean Squard Error, RMSE)

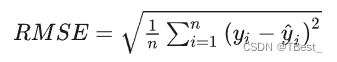
4.1.3 平均绝对误差（Mean Absolute Error, MAE)

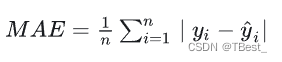
4.1.4 决定系数R-square (Coefficient of determination，$R^2$)

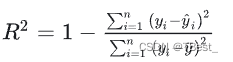
通过数据的变化来表征一个拟合的好坏

4.2 线性回归代码

from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
import math
 
# 对测试集进行预测
y_test_pred = model.predict(X_test)
# print(y_test_pred)
MSE = mean_squared_error(y_test_pred, y_test)  # 均方误差
RMSE = math.sqrt(MSE)
R2 = r2_score(y_test_pred, y_test)
MAE = mean_absolute_error(y_test_pred, y_test)
print(f'score:{model.score(X_test, y_test)}')
print(f'均方误差:{MSE}\n'
      f'均方根误差:{RMSE}\n'
      f'R2决定系数:{R2}\n'
      f'平方绝对误差:{MAE}')

4.3 决策树回归代码

from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
import math
 
# 对测试集进行预测
y_test_pred = model.predict(X_test)
# print(y_test_pred)
MSE = mean_squared_error(y_test_pred, y_test)  # 均方误差
RMSE = math.sqrt(MSE)
R2 = r2_score(y_test_pred, y_test)
MAE = mean_absolute_error(y_test_pred, y_test)
print(f'score:{model.score(X_test, y_test)}')
print(f'均方误差:{MSE}\n'
      f'均方根误差:{RMSE}\n'
      f'R2决定系数:{R2}\n'
      f'平方绝对误差:{MAE}')

4.4 总结

4.4.1 线性回归结果

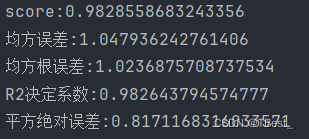
4.4.2 决策树回归结果

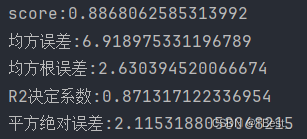
 4.4.3 结论

综上比较，可知一般线性回归模型拟合较好，预测数据准确率高于决策树回归。统一数据，不同模型，预测效果不同，可尝试多种模型进行训练预测。

五、总结

        线性回归假设特征与输出之间存在线性关系，并通过最小化残差平方和来拟合最优的参数。线性回归容易理解和实现，但要求特征与输出之间的关系是线性的。

        决策树回归基于树的叶节点上的均值或中位数来预测输出。决策树回归易于解释和理解，但容易过拟合。

六、源码

6.1 线性回归

from sklearn.linear_model import LinearRegression
import pandas as pd
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
from sklearn.model_selection import train_test_split
import math
import numpy as np
 
# 导入数据
data = pd.read_excel("height.xlsx").values
x_data = data[:, 0:2]
y_data = np.around(data[:, 2], 2)  # 身高保留两位小数
 
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(
    x_data, y_data,
    test_size=0.2,
    random_state=12
)
 
# 建立模型
model = LinearRegression()
model.fit(X_train, y_train)  # 使用训练集多模型进行训练
 
# 对测试机进行预测
predict = model.predict(X_test)
 
# 模型分析
MSE = mean_squared_error(predict, y_test)
RMSE = math.sqrt(MSE)
R2 = r2_score(predict, y_test)
MAE = mean_absolute_error(predict, y_test)
print(f'score:{model.score(X_test, y_test)}')
print(f'均方误差:{MSE}\n'
      f'均方根误差:{RMSE}\n'
      f'R2决定系数:{R2}\n'
      f'平方绝对误差:{MAE}')

6.2 决策树回归

from sklearn.tree import DecisionTreeRegressor
import pandas as pd
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
from sklearn.model_selection import train_test_split
import math
import numpy as np
 
# 导入数据
data = pd.read_excel("height.xlsx").values
x_data = data[:, 0:2]  # 取数据集种的前两列
y_data = np.around(data[:, 2], 2)  # 身高保留两位小数
 
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(
    x_data, y_data,
    test_size=0.2,
    random_state=12
)
 
# 建立模型
model = DecisionTreeRegressor(max_depth=3)
model.fit(X_train, y_train)  # 训练模型
 
# 对测试集进行预测
y_test_pred = model.predict(X_test)
# print(y_test_pred)
MSE = mean_squared_error(y_test_pred, y_test)  # 均方误差
RMSE = math.sqrt(MSE)
R2 = r2_score(y_test_pred, y_test)
MAE = mean_absolute_error(y_test_pred, y_test)
print(f'score:{model.score(X_test, y_test)}')
print(f'均方误差:{MSE}\n'
      f'均方根误差:{RMSE}\n'
      f'R2决定系数:{R2}\n'
      f'平方绝对误差:{MAE}')