平衡二叉树的插入调整_有一棵平衡二叉树,在其中添加1元素,构成新的平衡二叉树为

平衡二叉树

概念： 它或者是一颗空树，或它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1，且它的左子树和右子树都是一颗平衡二叉树。
平衡二叉树一定是二叉排序树！

平衡二叉树的插入调整

平衡二叉树中插入新节点方式与二叉排序树相似，只是插入后可能破坏了平衡二叉树的平衡性，有四种失衡失衡模式，则对应有四种调整方式：
在此先规定两个概念：
不平衡的发现者：在插入一个结点后，从下往上数的第一个平衡因子（左子树的高度-右子树的高度）变为2或者-2的结点。
麻烦结点：破坏了平衡的结点，就是刚刚插入的结点。

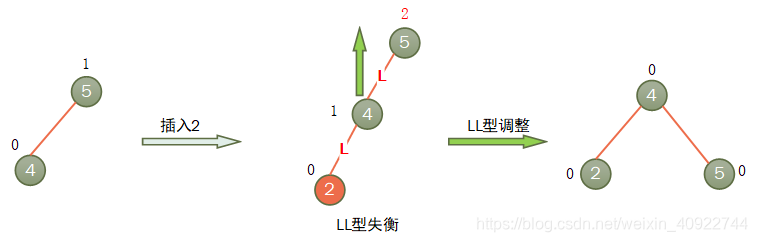
1. LL型调整
   LL型失衡：麻烦结点在不平衡发现者的左子树的左子树上，因而叫LL型插入，需要LL型调整；
   LL型调整：把不平衡发现者的左儿子提到不平衡发现者的位置，使他成为新的根，而不平衡发现者则插入到之前他左儿子的右儿子上，新根之前的右儿子插入到不平衡发现者的左儿子上面。
   具体图示如下：
   
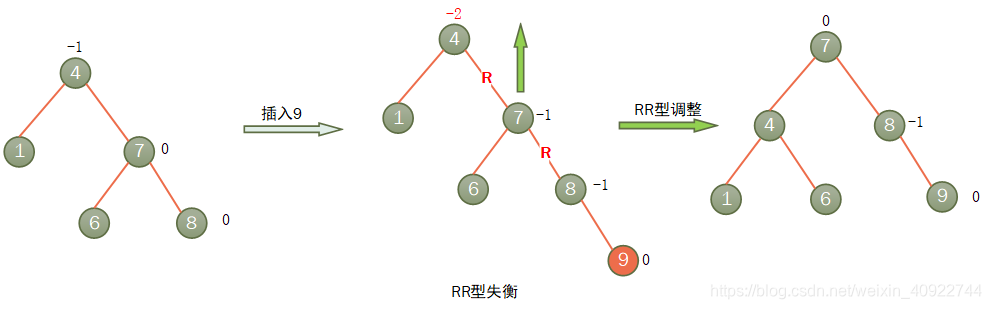
2. RR型调整
   RR型失衡：麻烦结点在不平衡发现者的右子树的右子树上，因而叫RR型插入，需要RR型调整。
   RR型调整：把不平衡发现者的右儿子提到不平衡发现者的位置，使他成为新的根，而不平衡发现者则插入到之前他右儿子的左儿子上，新根之前的左儿子插入到不平衡发现者的右儿子上面。
   具体图示如下：
   
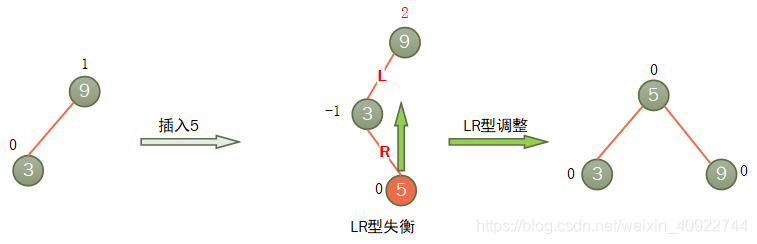
3. LR型调整
   LR型失衡：麻烦结点在不平衡发现者的左子树的右子树上，因而叫LR型插入，需要LR型调整。
   LR型调整：把不平衡发现者的左儿子的右儿子提到不平衡发现者的位置，使他成为新的根，不平衡发现者则插入到新根的右儿子上，而不平衡发现者的左儿子则插入到新根的左儿子上面，新根之前的右儿子则插入到不平衡发现者的左儿子上面。
   具体图示如下：
   
4. RL型调整
   RL型失衡：麻烦节点在不平衡发现者的右子树的左子树上，因而叫RL型插入，需要RL型调整。
   RL型调整：把不平衡发现者右儿子的左儿子提到不平衡发现者的位置，使他成为新的根，不平衡发现者则插入到新根的左儿子上，而不平衡发现者的右儿子则插入到新根的右儿子上面，新根之前的左儿子则插入到不平衡发现者的右儿子上面。
   具体图示如下：
   
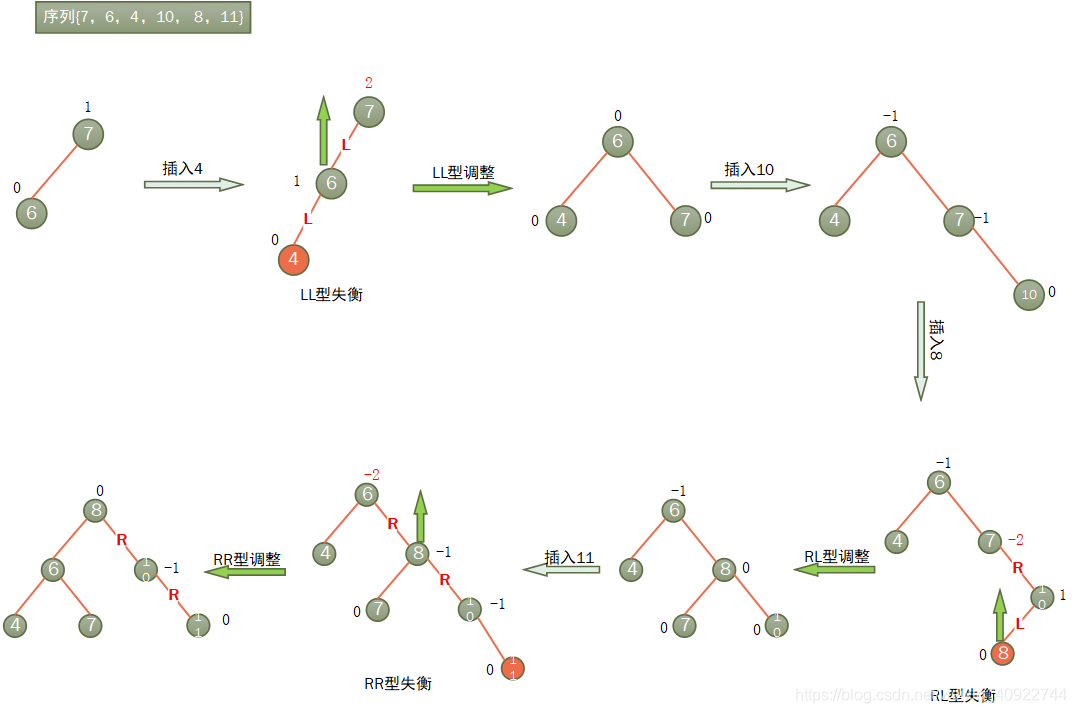
   平衡二叉树的构造实例：
   输入关键字序列{7，6，4，10， 8，11}， 给出构造一棵AVL树的步骤。
   具体图示如下：
   
   
   

特别鸣谢

• 各种结构的查找
• 平衡二叉树的调整