【算法整理】快慢指针-链表的环检测_链表的环的检测快慢指针

算法解决的问题

链表是编程中最常见的数据结构，当我们遍历链表时如果链表中存在闭环(如下图)，会造成无限循环的情况。为了解决这个问题我们需要在遍历之前对链表做环检测。

算法解决方案-快慢指针

我们设置两个指针如下图

然后快指针每次移动两个节点，慢指针每次移动一个节点，就像两个人在操场上跑，一个跑得快一个跑得慢，那么如果一直跑下去两人总会相遇。当两个指针相遇就代表链表存在闭环。此时的代码实现应该是这样的:

LinkedNode<T>* checkCycle()
{
	LinkedNode<T> *fast, *slow;
	fast = this->head;
	slow = this->head;

	while (fast->next != nullptr && fast->next->next != nullptr)
	{
		slow = slow->next;
		fast = fast->next->next;
		if (fast == slow)
		{
			std::cout << "存在闭环，相遇点的值：" << fast->value << std::endl;
			
			return fast;
		}
	}
	return nullptr;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

这个时候我们已经可以确定链表是否有闭环，那么在进一步我们还可以找到闭环的入口。就是上图6的节点。

闭环点分析

如下图所示，设链表中环外部分的长度为 L。指针进入环后，又走了 E的距离与 fast 相遇。此时，fast 指针已经走完了环的 n 圈,环长C。由于我们设定快指针是慢指针的2倍速度。因此有：R+E=n*C,演算过程如下：

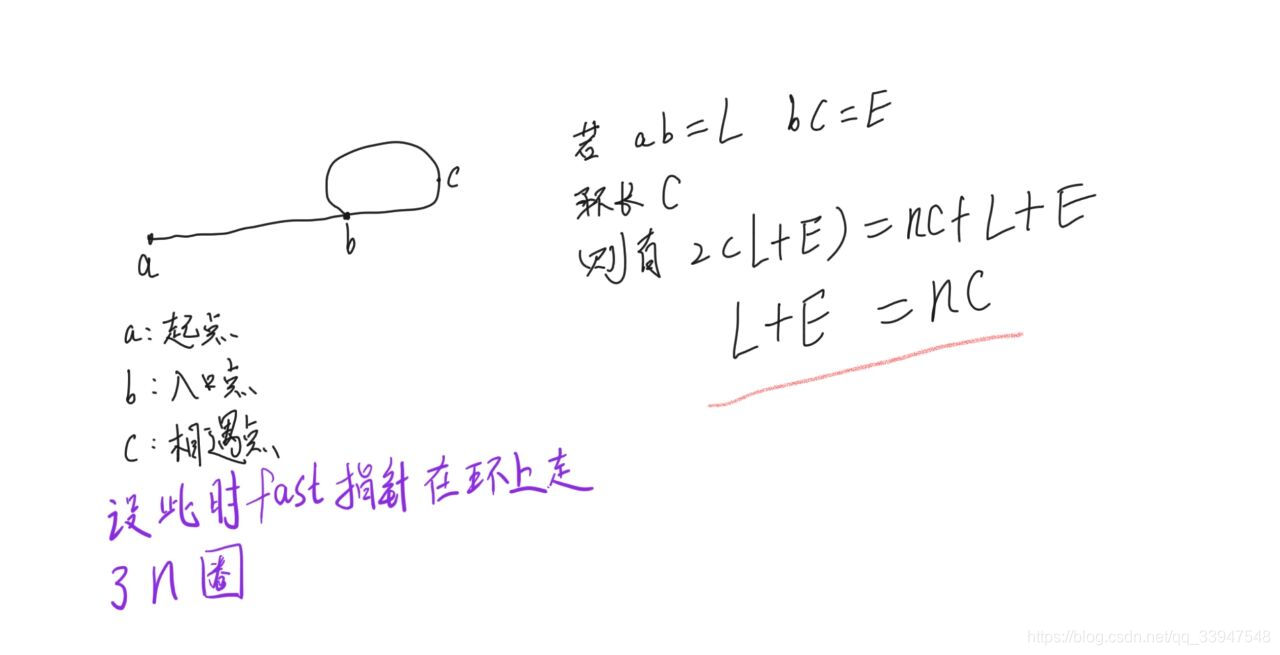
由以上结果可知：如果此时第三个指针以和慢指针一样的速度从链表头开始出发，它和慢指针一定会在c点相遇，那么可以得知它们的第一次相遇点就是环入口。进一步完善上面的代码：

LinkedNode<T>* checkCycle()
	{
		LinkedNode<T> *fast, *slow;
		fast = this->head;
		slow = this->head;

		while (fast->next != nullptr && fast->next->next != nullptr)
		{
			slow = slow->next;
			fast = fast->next->next;
			if (fast == slow)
			{
				std::cout << "存在闭环，相遇点的值：" << fast->value << std::endl;
				fast = this->head;
				while (fast != slow)
				{
					fast = fast->next;
					slow = slow->next;
				}
				std::cout << "环入口值: " << fast->value << std::endl;
				return fast;
			}
		}
		return nullptr;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

全部代码

/*
	List的单向链表实现
*/
template <class T>
class LinkedNode
{
public:
	T value;
	LinkedNode *next;
	LinkedNode(T value) {
		this->value = value;
		next = nullptr;
	}
	LinkedNode() {
		// value = default();
		next = nullptr;
	}
};


template <class T>
class LinkedList
{
public:
	LinkedNode<T> *head;
	LinkedList(LinkedNode<T> *head) {
		this->head = head;
	}

	// 尾插法
	bool add(LinkedNode<T> *node)
	{
		// 滑动指针
		LinkedNode<T> *temp = this->head;
		while (temp->next != nullptr)
		{
			temp = temp->next;
		}
		temp->next = node;
		return true;
	}
	bool add(T t)
	{
		LinkedNode<T> *node = new LinkedNode<T>(t);
		this->add(node);
		return true;
	}

	
	int size()
	{
		if (checkLoop() != nullptr)
		{
			// 存在闭环则返回-1
			return -1;
		}
		LinkedNode<T> *temp;
		temp = this->head;
		int size = 0;
		while (temp != nullptr)
		{
			size++;
			temp = temp->next;
		}
		return size;
	}

	LinkedNode<T>* checkLoop()
	{
		LinkedNode<T> *fast, *slow;
		fast = this->head;
		slow = this->head;

		while (fast->next != nullptr && fast->next->next != nullptr)
		{
			slow = slow->next;
			fast = fast->next->next;
			if (fast == slow)
			{
				std::cout << "存在闭环，相遇点的值：" << fast->value << std::endl;
				fast = this->head;
				while (fast != slow)
				{
					fast = fast->next;
					slow = slow->next;
				}
				std::cout << "环入口值: " << fast->value << std::endl;
				return fast;
			}
		}
		return nullptr;
	}
	// 遍历操作
	void foreach( void(*fun)(T item, int index)) const
	{

		LinkedNode<T> *temp = this->head->next;
		int i = 0;
		while (temp != nullptr)
		{
			
			fun(temp->value, i++);
			temp = temp->next;
		}

	}
	// 映射操作
	template<typename V> 
	LinkedList<V> map(V(*fun)(T item, int index))
	{
		LinkedList<V> newList(new LinkedNode<V>());

		LinkedNode<T> *temp = this->head->next;
		int i = 0;
		while (temp != nullptr)
		{

			V res = fun(temp->value, i++);
			newList.add(res);
			temp = temp->next;
		}
		return newList;
	}


	

};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128