从零实现机器学习算法（十二）DBSCAN_accord.machinelearning.cluseter.dbscanclusterer

作者：知新_RL | 2024-07-11 17:39:11

踩

accord.machinelearning.cluseter.dbscanclusterer

1. DBSCAN简介

1. DBSCAN简介

DBSCAN(Density-based spatial clustering of applications with noise）是一种基于密度的聚类算法。与划分和层次聚类方法不同，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇。KMeans对于非球状的数据聚类效果不好，但DBSCAN可在噪声的空间数据库中发现任意形状的聚类。

2. DBSCAN模型

2.1 相关名词

首先介绍几个概念：

$\varepsilon$ -邻域：对于某一对象点来说，在其半径为 $\varepsilon$ 的区域为 $\varepsilon$ -邻域。

核心对象：对于给定的数目 $m$ ，如果一个对象的 $\varepsilon$ -邻域内至少包含 $m$ 个对象，那么称该对象为核心对象。

直接密度可达：给定一个集合 $D$ ，如果 $P$ 是在 $Q$ 的 $\varepsilon$ -邻域内而且 $Q$ 是一个核心对象，那么对象 $Q$ 从对象 $P$ 出发是直接密度可达( $P$ 可以是核心对象也可以不是)

密度可达：如果存在一个对象链 $P_{1}P_{2}...P_{n}$ , $P=P_{1}$ , $Q=P_{n}$ 。如果 $P_{i}$ 从 $P_{i-1}$ 直接密度可达，那么对象 $Q$ 从对象 $P$ 出发是直接密度可达(直接密度可达就是对象 $P$ 在 $Q$ 的邻域内，而密度可达对象 $P$ 不在 $Q$ 的邻域内）

密度相联：存在样本集合 $D$ 中的一点 $O$ ，如果对象 $O$ 到对象 $P$ 和对象 $Q$ 都是密度可达的，那么 $P$ 和 $Q$ 密度相联。

噪声：与任何点都不可达的对象称为噪声

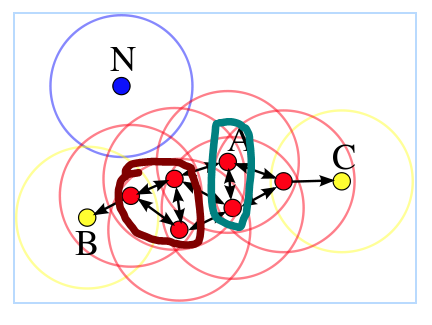
举个例子, 如图所示, 其中 $m=4$ ，圆形范围为 $\varepsilon$ -邻域。由于图中红色的点的 $\varepsilon$ -邻域内都存在至少四个点，因此它们都是核心对象, 并且它们都是密度可达。 $B,C$ 由于邻域内的点少于四个因此它们不是核心对象。图中青色圈中的点是直接密度可达的。图中褐色的圈中的点是密度相联。由于 $N$ 与任何点都不可达，因此它是噪声点。

2.2聚类算法

首先我们通过计算所有样本的 $\varepsilon$ -邻域内样本数目找出数据集中所有的核心对象，剩余的样本点暂时记为噪声点。这里的距离可以使用欧式距离也可以使用其他距离，本文采用的是欧式距离。


    def getCenters(self, train_data):
        neighbor = {}
        for i in range(len(train_data)):
            distance = self.calculateDistance(train_data[i], train_data)
            index = np.where(distance <= self.eps)[0]
            if len(index) > self.m:
                neighbor[i] = index
        return neighbor

然后我们任一选取一个未被访问的核心对象 $P$ ，开始合并与它密度相联的所有其他的点。即依次访问被选择核心对象邻域内的点 $Q$ ，首先判断 $Q$ 点是否为核心对象，如果 $Q$ 是核心对象，则将该点领域中的点划为 $P$ 所属的簇，然后对 $Q$ 进行相同的操作（有点像深度优先遍历）。如果该点不是核心对象，那么访问下一个点，示意图如下。

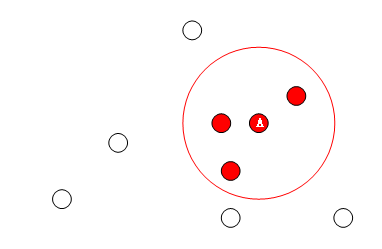
选取核心对象A点，找出其邻域内的所有样本，都属于簇A，依次访问领域内的点

访问A邻域内的点B，点B是核心对象，访问B邻域内的点

访问B领域内的点C，C属于簇A，C不是核心对象，访问B领域的其他点

访问B领域内另一个样本点D，D是核心对象，访问D领域内的点

访问E，E不是核心对象，此时没有其他点与簇A密度可达，停止簇A聚类。


        k = 0
        unvisited = list(range(sample_num))               # samples which are not visited
        while len(centers) > 0:
            visited = []
            visited.extend(unvisited)
            cores = list(centers.keys())
            # choose a random cluster center
            randNum = np.random.randint(0, len(cores))
            core = cores[randNum]
            core_neighbor = []                              # samples in core's neighbor
            core_neighbor.append(core)
            unvisited.remove(core)
            # merege the samples density-connectivity
            while len(core_neighbor) > 0:
                Q = core_neighbor[0]
                del core_neighbor[0]
                if Q in initial_centers.keys():
                    diff = [sample for sample in initial_centers[Q] if sample in unvisited]
                    core_neighbor.extend(diff)
                    unvisited = [sample for sample in unvisited if sample not in diff]
            k += 1
            label[k] = [val for val in visited if val not in unvisited]
            for index in label[k]:
                if index in centers.keys():
                    del centers[index]

2.3 参数选择

DBSCAN包括两种参数一种是领域大小 $\varepsilon$ 它决定了样本点簇之间的距离，另一个参数是 $m$ 它决定了每个簇应该包含多少个样本。对于 $\varepsilon$ ，我们计算每个样本到同一个领域内最近样本点的距离，并画出直方图。我们可以看到在大多数样本满足距离小于22这一条件，因此 $\varepsilon=22$