强化学习的基本求解方法(一)_强化算法求解复杂函数的极值

1. 简介

上一节主要介绍了强化学习的基本概念，主要是通过设定场景带入强化学习的策略、奖励、状态、价值进行介绍。有了基本的元素之后，就借助马尔可夫决策过程将强化学习的任务抽象出来，最后使用贝尔曼方程进行表述。本次内容主要是介绍强化学习的求解方法。也等同于优化贝尔曼方程。

2. 贝尔曼方程

首先我们回顾一下贝尔曼方程。贝尔曼方程可以用于表示在当前时刻t状态的价值和下一时刻t+1状态的价值之间的关系。因此状态值函数v(s)和动作值函数q(s,a)的动态关系都可套用贝尔曼方程进行表示。

这里以状态值函数v(s)为例使用贝尔曼方程进行表示。那么就需要将式子1进行带入，整体可以分为两个部分：第一部分可以理解为即时的奖励rt；另一部分表示的是未来状态的折扣价值γv(st+1)：

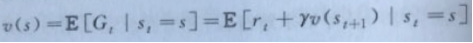
式子1

那么，状态值函数的贝尔曼方程进化变成为：

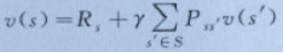
式子2

式子2表示当前状态s的价值函数，由当前状态获得的奖励Rs加上经过状态间转换概率Pss`乘以下一状态的状态值函数v(s`)得到，其中γ是未来折扣因子。最后可以将表达式简化为式子3的形态：