python GUI 编程_python gui编程

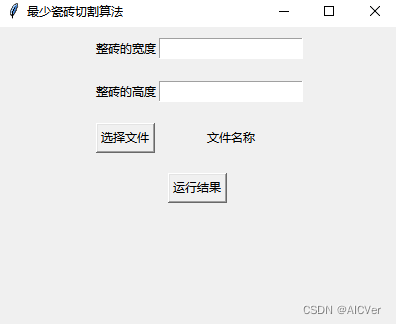
界面程序

"""测试一个经典的GUI程序的写法，使用面向对象的方式"""
import time
from tkinter import *
from tkinter import messagebox
from tkinter import filedialog
import threading
from cut_brick import cal_brick

class Application(Frame):
    """一个经典的GUI程序的类的写法"""
    def __init__(self, master=None):
        super().__init__(master)      #super()代表的是父类的定义，而不是父类对象
        self.master=master
        self.pack()
        self.createWidget()
        self.file_name = ""

    def createWidget(self):
        """创建组件"""
        self.result = Label(self,text="")

        self.label_width = Label(self, text="整砖的宽度")
        self.label_height = Label(self, text="整砖的高度")
        self.width_entry = Entry(self)
        self.height_entry = Entry(self)

        self.label_width.grid(row=0, column=0,pady=10)
        self.width_entry.grid(row=0, column=1,pady=10)
        self.label_height.grid(row=1, column=0,pady=10)
        self.height_entry.grid(row=1, column=1,pady=10)

        self.select_file = Button(self,text="选择文件", command=self.select_file_path)
        self.file_path = Label(self, text="文件名称")
        self.select_file.grid(row=2, column=0, pady=10)
        self.file_path.grid(row=2, column=1, pady=10)

        self.btn01 = Button(self)
        self.btn01["text"] = "运行结果"
        self.btn01["command"] = self.cal_brick_num
        self.btn01.grid(row=3, column=0, columnspan=2,pady=10)
        self.result.grid(row=4, column=0, columnspan=2,pady=10)
        # 创建一个退出按钮
        # self.btnQuit= Button(self, text="退出", command=root.destroy)
        # self.btnQuit.pack()

    def cal_brick_num(self):
        def run():
            self.result["text"] = "运行中"
            self.btn01.config(state=DISABLED)
            save_path = self.file_name.replace(self.file_path["text"], "") + "cut_img\\"
            excel_file_path = self.file_name

            brick_num = cal_brick(excel_file_path,int(input_width),int(input_height), save_path)
            self.result["text"] = "所需砖数为" + str(brick_num)
            self.btn01.config(state=NORMAL)

        input_width = self.width_entry.get()
        input_height = self.height_entry.get()
        if input_width == "" or input_height == "" or self.file_name == "":
            messagebox.showinfo("提示", "存在输入为空，请检查输入！")
            return

        # 创建
        t = threading.Thread(target=run)
        t.setDaemon(True)
        t.start()



    def select_file_path(self):
        img_path = filedialog.askopenfilename()
        self.file_name = img_path
        self.file_path["text"] = img_path.split("/")[-1]


if __name__ == "__main__":
    root=Tk()
    root.geometry("400x300+200+300")
    root.title("最少瓷砖切割算法")
    app = Application(master=root)
    root.mainloop()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

其它文件

1. cut_brick.py

# coding=utf-8
import sys,os
from tools import *
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import random
# matplotlib.use('Agg')

Bin=[600,600] #箱子宽度与高度
excel_path = "D:\project\C\LayoutAapter\Layout\data\dong\\floor3\\237\\brick.xlsx"
img_save_path = "D:\\Data\\myimg\\brick_img\\"
sheet_name = "整层"

def draw_bin(AllItem,RPNXY,name_index = 0):
    global img_save_path
    fig, ax = plt.subplots(1, 1)
    ax1 = fig.gca()
    for i in RPNXY:
        width,height = AllItem[i[0]]
        rx,ry = i[1],i[2]
        lx,ly = rx-width,ry-height
        plt.xlim((0, Bin[0]))
        plt.ylim((0, Bin[1]))
        color = "#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])
        rect = patches.Rectangle((lx, ly), width,height,linewidth=1, facecolor = color)
        ax1.text(lx + width/2 - 30, ly + height / 2, str(width) + "*" + str(height))
        ax1.add_patch(rect)
    plt.savefig(img_save_path + str(name_index) + ".jpg")
    # plt.show()
    # plt.imsave(str(name_index) + ".png",fig)
    plt.close()


def arr_sort(AllItem):
    item_dict = {}
    for i in range(len(AllItem)):
        item_dict[i] = AllItem[i].copy()
    item_dict = dict(sorted(item_dict.items(), key=lambda x: -x[1][1]))

    for i, key in enumerate(item_dict.keys()):
        # print(i, item_dict[key])
        AllItem[i] = item_dict[key]
    # print(AllItem)
    return AllItem


def get_all_item_by_excel(file_path=None):
    import pandas as pd

    global excel_path,sheet_name
    if file_path is None:
        file_path = excel_path

    xlsx = pd.ExcelFile(file_path)
    # sheet_name = "整层"
    # print(pd.read_excel(xlsx, sheet_name))
    df = pd.read_excel(xlsx, sheet_name)
    AllItem = []
    for i in range(len(df) - 1):
        print(df.iloc[i,0],df.iloc[i,1])
        brick_size = np.asarray(df.iloc[i,0].split("*")[:2],dtype=int)
        for j in range(int(df.iloc[i,1])):
            if sum(brick_size) == sum(Bin):
                continue
            AllItem.append(brick_size)
    return np.asarray(AllItem)


def get_data_by_excel(file_path=None):
    import pandas as pd

    global excel_path
    if file_path is None:
        file_path = excel_path

    xlsx = pd.ExcelFile(file_path)

    if file_path.__contains__("floor"):
        sheet_name = "整层"
    else:
        sheet_name = "整栋"
    print(pd.read_excel(xlsx, sheet_name))
    df = pd.read_excel(xlsx, sheet_name)

    AllItem = []
    for i in range(len(df) - 1):
        print(df.iloc[i,0],df.iloc[i,1])
        brick_size = np.asarray(df.iloc[i,0].split("*")[:2],dtype=int)
        brick_size[np.where(brick_size>600)] = 600
        for j in range(int(df.iloc[i,1])):
            if sum(brick_size) == sum(Bin):
                continue
            AllItem.append(brick_size)
    box_size = [Bin]
    return box_size, AllItem


def get_1D_data_by_excel(file_path=None):
    import pandas as pd

    global excel_path
    if file_path is None:
        file_path = excel_path

    xlsx = pd.ExcelFile(file_path)

    if file_path.__contains__("floor"):
        sheet_name = "整层"
    else:
        sheet_name = "整栋"
    print(pd.read_excel(xlsx, sheet_name))
    df = pd.read_excel(xlsx, sheet_name)

    AllItem = []
    for i in range(len(df) - 1):
        print(df.iloc[i,0],df.iloc[i,1])
        brick_size = np.asarray(df.iloc[i,0].split("*")[:2],dtype=int)
        brick_size[np.where(brick_size>600)] = 600
        for j in range(int(df.iloc[i,1])):
            AllItem.append(brick_size[1])
    box_size = [Bin[0]]
    return box_size, AllItem


def put_bin(AllItem):
    #   BL（bottom-up left-justified）法求解二位装箱问题
    #   @BetterBench
    #   思想：首先将选中的物体放在箱子的右上角，然后尽量向下向左作连续移动，直到不能移动为止
    # 输入参数
    itemNum=len(AllItem) #物品数目

    ran=list(range(itemNum))
    # random.shuffle(ran) #随机生成装箱序列
    AllItem = arr_sort(AllItem)

    ansBXY=np.zeros((itemNum,3))  #[箱子编号，X坐标，Y坐标]

    boxes = []
    RPNXY=[]
    BinNum=0
    flagItem=np.zeros(itemNum) #标记物品是否被装入箱子，0没有装入，1装入
    # 开始装箱

    for i in range(itemNum):
        if flagItem[ran[i]]==0:
            item=AllItem[ran[i],:]
            itemRP=Bin  #起点全部在箱子右上角顶点
            is_put = False
            for j in range(len(boxes)):
                RPNXY = boxes[j]
                flagOL=overlap(item,AllItem,itemRP,RPNXY) #如果重合flagOL=1；反之flagOL=0
                if flagOL==0:
                    itemRP=finalPos(item,AllItem,itemRP,RPNXY) #更新物品从当前位置向下向左移动后到最终位置后右上角顶点坐标
                    if len(itemRP)>0:
                        RPNXY.append([ran[i],itemRP[0],itemRP[1]])
                        flagItem[ran[i]]=1
                        boxes[j] = RPNXY
                        is_put = True
                        break
            # 启用第下一个箱子
            if not is_put:
                BinNum=BinNum+1
                RPNXY=[[ran[i], item[0], item[1]]]
                flagItem[ran[i]] = 1
                boxes.append(RPNXY)

    return boxes,AllItem


def cal_brick(file_name, width, height, save_path):
    global excel_path,Bin,img_save_path
    excel_path = file_name
    Bin = [width, height]
    img_save_path = save_path
    if not os.path.exists(save_path):
        os.mkdir(save_path)

    for file_name in os.listdir(img_save_path):
        os.remove(img_save_path+file_name)

    all_items = get_all_item_by_excel()
    boxes,AllItem = put_bin(all_items)
    for index in range(len(boxes)):
        draw_bin(AllItem,boxes[index],index)
    return len(boxes)


if __name__ == "__main__":
    # global Bin,excel_path,img_save_path

    argv_path = None
    argv_save_path = None
    argv_width = None
    excel_sheet_name = None

    for index in range(1, len(sys.argv)):
        if index == 1:
            argv_path = sys.argv[1]
        if index == 2:
            argv_save_path = sys.argv[2]
        if index == 3:
            argv_width = sys.argv[3]
        if index == 4:
            excel_sheet_name = sys.argv[4]

    if argv_width is not None:
        Bin = [int(argv_width),int(argv_width)]

    if argv_path is not None:
        excel_path = argv_path

    if argv_save_path is not None:
        img_save_path = argv_save_path

    if excel_sheet_name is not None:
        sheet_name = excel_sheet_name

    for file_name in os.listdir(img_save_path):
        os.remove(img_save_path + file_name)

    all_items = get_all_item_by_excel()
    boxes, AllItem = put_bin(all_items)
    print(len(boxes))
    for index in range(len(boxes)):
        draw_bin(AllItem, boxes[index], index)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226

2. tools.py

# -*- coding: UTF-8 -*-
import numpy as np

def Horizontal_Lines_Intersect(line1,line2):
    # 判断两条水平线段经过竖直移动后是否会相交，如果相交，计算两条水平线段竖直距离是多少
    # 思路：分5种情况：1）左方不相交；2）左方相交；3）右方相交；4）右方不相交；5）line1完全包含line2
    # 输入line1：  第一条线段[x1,y1,x2,y2]
    # 输入line2：  第二条线段[x1,y1,x2,y2]
    # 输出flag：  判断两条水平线段经过竖直移动后是否会相交，flag=1相交，flag=0不相交
    # 输出HD：  两条竖直线段距离是多少，如果平移动后相交，HD为正数，反之为负数
    #第一种情况，line1完全在line2左方，即line1右端顶点x坐标小于等于line2左端顶点x坐标，且两条线段经过竖直移动后不会相交
    if line1[2]<=line2[0]:
        flag=0
        HD=line1[1]-line2[1]
    #第二种情况，line1在line2左方，即line1右端顶点x坐标大于line2左端顶点x坐标且小于等于且line2右端顶点x坐标，但两条线段经过竖直移动后会相交
    elif (line1[2]>line2[0]) and (line1[2]<=line2[0]):
        flag=1
        HD=line1[1]-line2[1]
    #第三种情况，line1在line2右方，即line1左端顶点x坐标大于等于line2左端顶点x坐标且小于且line2右端顶点x坐标，但两条线段经过竖直移动后会相交
    elif (line1[0]>=line2[0]) and (line1[0]<line2[2]):
        flag=1
        HD=line1[1]-line2[1]
    #第四种情况，line1完全在line2右方，即line1左端顶点x坐标大于等于line2右端顶点x坐标，且两条线段经过竖直移动后不会相交
    elif line1[0]>=line2[2]:
        flag=0
        HD=line1[1]-line2[1]
    #第五种情况，line1完全包含line2，即line1左端顶点x坐标小于等于line2左端顶点x坐标，
    #line1右端顶点x坐标大于等于line2右端顶点x坐标，且两条线段经过竖直移动后会相交
    else:
        flag=1
        HD=line1[1]-line2[1]
    return flag,HD

######################################
# 根据物品右上角顶点坐标和物品宽度和高度，求出物品下端水平线段左右两端坐标[leftx,lefty,rightx,righty]
# 输入item：  物品[宽度，高度]
# 输入RPXY：物品右上角顶点坐标[x,y]
# 输出leftLine：  物品下端水平线段左右两端坐标[leftx,lefty,rightx,righty]
def Point_Horizontal_Line(item,RPXY):
    RBPXY=[RPXY[0],RPXY[1]-item[1]]#  物品右下角顶点坐标
    LBPXY=[RPXY[0]-item[0],RPXY[1]-item[1]]  #物品左下角顶点坐标
    bottomLine=[]
    bottomLine.extend(LBPXY)
    bottomLine.extend(RBPXY)
    return bottomLine

# 计算在当前箱子中，物品item在箱子内任意位置可以下降的最大高度
# 输入item：   物品[宽度，高度]
# 输入AllItem：   各个物品[宽度，高度]
# 输入itemRP： 此时物品右上角顶点坐标[x,y]
# 输入RPNXY：  当前箱子中所有物品右上角顶点坐标数组
# 输出downH：  物品item在箱子内任意位置可以下降的最大高度（如果能装入当前箱子，则downH为正数；如果不能装入当前箱子，则为负数）
def downHAtPoint(item,AllItem,itemRP,RPNXY):
    bottomLine=Point_Horizontal_Line(item,itemRP)  #物品下端水平线段左右两端坐标[leftx,lefty,rightx,righty]
    RP_NUM=len(RPNXY) #箱子内物品数目
    if RP_NUM!=0:
        sRPNXY=np.array(sorted(list(RPNXY), key=lambda x:x[2],reverse=True))#将RPNXY按照Y坐标降序排列
        sRBPNXY=sRPNXY.copy()
        sRBPNXY[:,1]=sRPNXY[:,1]-AllItem[sRPNXY[:,0],0]  #将RPNXY按照Y坐标降序排列后的左上角顶点坐标
        
        topLine=np.concatenate((sRBPNXY[:,1:3],sRPNXY[:,1:3]),axis=1)  #物品按照Y坐标降序排列后，物品上端水平线段左右两端坐标[leftx,lefty,rightx,righty]
        # 逐个遍历sRPNXY中的物品
        alldownH=[]  # 储存所有满足相交条件的下降距离
        for i in range(RP_NUM):
            #判断两条水平线段经过竖直移动后是否会相交，flag=1相交，flag=0不相交
            #两条水平线段距离是多少，如果竖直移动后相交，HD为正数，反之为负数
            flag,HD=Horizontal_Lines_Intersect(bottomLine,topLine[i,:])
            if (flag==1) and (HD>=0):
                alldownH.append(HD)
        # 如果不存在满足相交条件的物品，则直接下降到箱子最底端
        if len(alldownH)==0:
            downH=itemRP[1]-item[1]
        else:  # 如果存在满足相交条件的物品，则下降距离为alldownH中的最小值
            downH=min(alldownH)
    else:
        downH=itemRP[1]-item[1]  #此时箱子没有物品，物品直接下降到箱子底端
    return downH

# 判断两条竖直线段经过水平移动后是否会相交，如果相交，计算两条竖直线段水平距离是多少
# 思路：分5种情况：1）上方不相交；2）上方相交；3）下方相交；4）下方不相交；5）line1完全包含line2
# 输入line1：  第一条线段[topx,topy,bottomx,bottomy]
# 输入line2：  第二条线段[topx,topy,bottomx,bottomy]
# 输出flag：  判断两条竖直线经过水平移动后是否会相交，flag=1相交，flag=0不相交
# 输出HD：  两条竖直线段距离是多少，如果平移动后相交，HD为正数，反之为负数
def Vertical_Lines_Intersect(line1,line2):
    # 第一种情况，line1完全在line2上方，且两条线段经过平移后不会相交
    if line1[3]>=line2[1]:
        flag=0
        HD=line1[0]-line2[0]
    # 第二种情况，line1在line2上方，但两条线段经过平移后会相交
    elif (line1[3]<line2[1])and (line1[3]>=line2[3]):
        flag=1
        HD=line1[0]-line2[0]
    # 第三种情况，line1在line2下方，但两条线段经过平移后会相交
    elif (line1[1]<=line2[1]) and (line1[1]>line2[3]):
        flag=1
        HD=line1[0]-line2[0]
    # 第四种情况，line1完全在line2下方，且两条线段经过平移后不会相交
    elif line1[1]<=line2[3]:
        flag=0
        HD=line1[0]-line2[0]
    else:
        flag=1
        HD=line1[0]-line2[0]
    return flag,HD

# 根据物品右上角顶点坐标和物品宽度和高度，求出物品左端竖直线段上下两端坐标[topx,topy,bottomx,bottomy]
# 输入item：  物品[宽度，高度]
# 输入RPXY：物品右上角顶点坐标[x,y]
# 输出leftLine：  物品左端竖直线段上下两端坐标[topx,topy,bottomx,bottomy]
def Point_Vertical_Line(item,RPXY):
    LUPXY=[RPXY[0]-item[0],RPXY[1]]  #物品左上角顶点坐标
    LBPXY=[RPXY[0]-item[0],RPXY[1]-item[1]] #物品左下角顶点坐标
    leftLine=[]
    leftLine.extend(LUPXY)
    leftLine.extend(LBPXY)
    return leftLine

# 计算在当前箱子中，物品item在箱子内任意位置可以向左移动的最大距离
# 输入item：   物品[宽度，高度]
# 输入Item：   各个物品[宽度，高度]
# 输入itemRP： 此时物品右上角顶点坐标[x,y]
# 输入RPNXY：  当前箱子中所有物品右上角顶点坐标数组
# 输出leftW：  物品item在箱子内任意位置可以向左移动的最大距离
def leftWAtPoint(item,Item,itemRP,RPNXY):
    leftLine=Point_Vertical_Line(item,itemRP)  #物品左端竖直线段上下两端坐标[topx,topy,bottomx,bottomy]
    RP_NUM=len(RPNXY)#箱子内物品数目
    if RP_NUM!=0:
        sRPNXY=np.array(sorted(list(RPNXY), key=lambda x:x[0]))  #将RPNXY按照X坐标降序排列
        sRBPNXY=sRPNXY.copy()
        sRBPNXY[:,2]=sRPNXY[:,2]-Item[sRPNXY[:,0],1] #将RPNXY按照X坐标降序排列后的右下角顶点坐标
        rightLine=np.concatenate((sRPNXY[:,1:3],sRBPNXY[:,1:3]),axis=1)#物品按照X坐标降序排列后，右端线段上下两端坐标[topx,topy,bottomx,bottomy]
        #逐个遍历sRPNXY中的物品
        allLeftW=[]  #储存所有满足相交条件的左移距离
        for i in range(RP_NUM):
            #判断两条竖直线经过水平移动后是否会相交，flag=1相交，flag=0不相交
            #两条竖直线段距离是多少，如果平移动后相交，HD为正数，反之为负数
            flag,HD=Vertical_Lines_Intersect(leftLine,rightLine[i,:])
            if (flag==1) and (HD>=0):
                allLeftW.append(HD)
        # 如果不存在满足相交条件的物品，则直接移动箱子最左端
        if len(allLeftW)==0:
            leftW=itemRP[0]-item[0]
        else: #如果存在满足相交条件的物品，则左移距离为allLeftW中的最小值
            leftW=min(allLeftW)
    else:
        leftW=itemRP[0]-item[0]
    return leftW

# 计算物品在箱子中从右上角下降downH又向左移动leftW后，右上角顶点的坐标
# 输入itemRP： 此时物品右上角顶点坐标[x,y]
# 输入downH：  物品item从右上角可以下降的最大高度
# 输入leftW：  物品item从右上角下降最大高度以后，可以向左移动的最大距离
# 输出itRPXY： 物品item在箱子中下降downH又向左移动leftW后，右上角顶点的坐标
def Update_itemRP(itemRP,downH,leftW):
    h=itemRP[1]-downH  #y坐标
    w=itemRP[0]-leftW   #x坐标
    return [w,h]
# 矩形类，[x,y,width,height]左下角坐标、长和宽
class Rectangle:
    def __init__(self, x, y,w,h):
      self.x = x
      self.y = y
      self.width = w
      self.height = h
# 计算物品从当前位置向下向左移动后到最终位置后右上角顶点坐标
# 输入item：   物品[宽度，高度]
# 输入Item：   各个物品[宽度，高度]
# 输入itemRP： 此时物品右上角顶点坐标[x,y]
# 输入RPNXY：  当前箱子中所有物品右上角顶点坐标数组
# 输出finalRP：物品item在箱子内任意位置向下向左移动后到最终位置后右上角顶点坐标
def finalPos(item,Item,itemRP,RPNXY):
    # 当物品item不能再继续下降或不能继续左移的时候，跳出循环
    while 1:
        downH=downHAtPoint(item,Item,itemRP,RPNXY) #计算物品item在箱子内itemRP位置处可以下降的最大高度
        leftW=0
        itemRP=Update_itemRP(itemRP,downH,leftW) #更新物品item当前位置右上角顶点坐标
        downH=0
        leftW=leftWAtPoint(item,Item,itemRP,RPNXY) #计算物品item在箱子内itemRP位置处可以向左移动的最大距离
        itemRP=Update_itemRP(itemRP,downH,leftW) #更新物品item当前位置右上角顶点坐标
        if (downH==0)and (leftW==0):
            finalRP=itemRP
            break
    return finalRP

# 判断物品item在当前位置itemRP与箱子中其他物品是否有重合
# 输入item：   物品[宽度，高度]
# 输入Item：   各个物品[宽度，高度]
# 输入itemRP： 此时物品右上角顶点坐标[x,y]
# 输入RPNXY：  当前箱子中所有物品右上角顶点坐标数组
# 输出flagOL： 如果重合flagOL=1；反之flagOL=0
def overlap(item,Item,itemRP,RPNXY):
    flagOL=0  # 初始化不存在重合情况
    itemLBP=[itemRP[0]-item[0],itemRP[1]-item[1]] #左下角顶点坐标
    A = Rectangle(itemLBP[0],itemLBP[1],item[0],item[1])
    num=len(RPNXY) # 箱子中物品数目
    if num>0:
        for i in range(num):
            width=Item[RPNXY[i][0],0]  #Item(RPNXY(i,1),:)宽度
            height=Item[RPNXY[i][0],1]  #Item(RPNXY(i,1),:)高度
            LBPXY=[RPNXY[i][1]-width,RPNXY[i][2]-height]  #在箱子中的当前矩形Item(RPNXY(i,1),:)的左下角顶点坐标
            B = Rectangle(LBPXY[0],LBPXY[1],width,height)
            area=rectint(A,B)#计算物品A与B相交的面积
            #如果AB相交，则满足下列关系
            if area>0:
                flagOL=1
                break
    return flagOL
# 计算两个矩形相交的面积，和MATLAB中rectint函数作用一样
def rectint(rect1, rect2):
    xl1, yb1, xr1, yt1 = rect1.x,rect1.y,rect1.x+rect1.width,rect1.y+rect1.height # （xl1, yb1）为矩形左下角坐标， （xr1, yt1）为右上角坐标
    xl2, yb2, xr2, yt2 = rect2.x,rect2.y,rect2.x+rect2.width,rect2.y+rect2.height # （xl2, yb2）为矩形左下角坐标， （xr2, yt2）为右上角坐标
    xmin = max(xl1, xl2)
    ymin = max(yb1, yb2)
    xmax = min(xr1, xr2)
    ymax = min(yt1, yt2)
    width = xmax - xmin
    height = ymax - ymin
    if width <= 0 or height <= 0:
        return 0
    cross_square = width * height
    return cross_square
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222