kmeans聚类算法_聚类算法之——K-Means算法

聚类算法属于无监督学习，它将相似的对象归到同一个簇中。K-Means算法是聚类算法中最常用到算法；

1. 预备知识点

距离计算

闵可夫斯基距离

点

之间的闵可夫斯基距离为

欧式距离

点

之间的欧氏距离为：

曼哈顿距离（Manhattan Distance ）

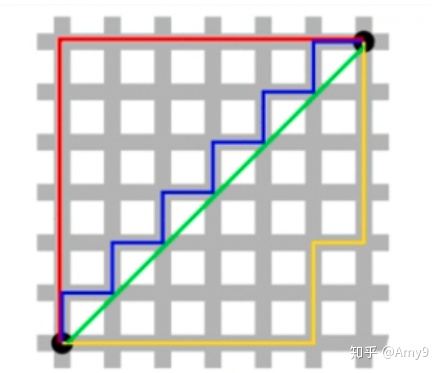
图中红线代表曼哈顿距离，绿线代表欧式距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。

曼哈顿距离：两点在南北方向上的距离加上在东西方向上的距离。

点

之间的曼哈顿距离为：

余弦距离

两个向量 A 和 B，其余弦距离（即两向量夹角的余弦）由点积和向量长度给出，计算公式如下：

其中，

分别代表向量 A 和 B 的各分量 。

2. K-Means算法步骤

输入：样本集{

}

​ 聚类簇数k

输出：簇划C={

}

1. 随机初始化k个点作为簇质心；
2. 将样本集中的每个点分配到一个簇中；
   计算每个点与质心之间的距离（常用欧式距离和余弦距离），并将其分配给距离最近的质心所对应的簇中；
3. 更新簇的质心。每个簇的质心更新为该簇所有点的平均值；
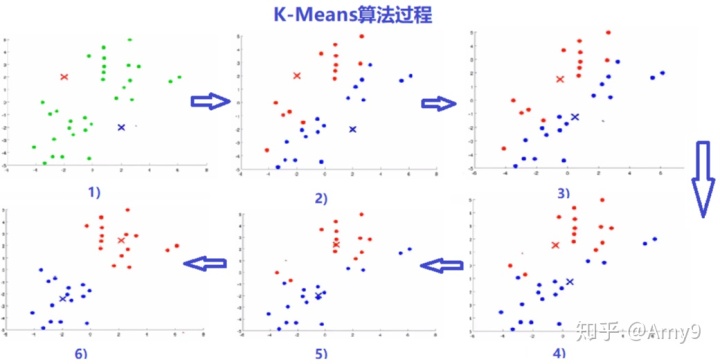
4. 反复迭代2 - 3 步骤，直到达到某个终止条件；
   常用的终止条件有：1）达到指定的迭代次数；2）簇心不再发生明显的变化，即收敛；3）最小误差平方和SSE；

3. 聚类效果的评价指标SSE

SSE(Sum of Square Error, 误差平方和)，SSE值越小表示数据点越接近于它们的质心，聚类效果也越好。

4. python脚本

调用sklearn包里的K-Means算法来实现

完整版脚本，直接运行即可

import 

运行结果

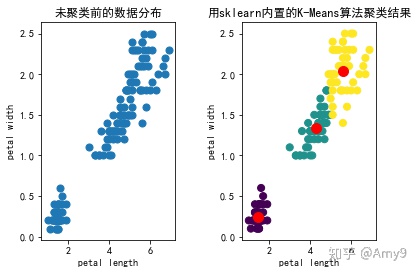
按原理来实现K-Means算法

import 

运行结果

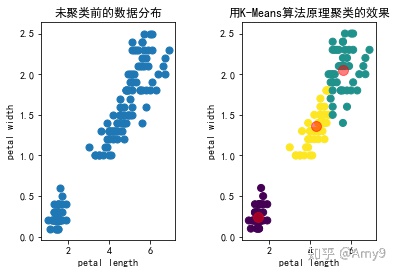
算法优缺点和适用场景

优点：容易实现

缺点：可能收敛到局部最小值，在大规模数据集上收敛较慢

适用数据类型：数值型数据

如何避免陷入局部最优

1. 当k=2~10之间时，可运行多次，一般次数在50到1000之间，在得到的多个损失函数中选取最小的；
   例如：循环100次，选取损失函数最小的那个聚类结果作为最终的聚类结果；
   for i =1 to 100: 随机初始化中心点； 运行k-means算法步骤； 计算损失函数J（即第3部分的误差平方和SSE）；
   选取损失函数最小的那个聚类结果作为最终的聚类结果；
2. 当k比较大时，不建议采取（1）的方法。

如何选择K的数量

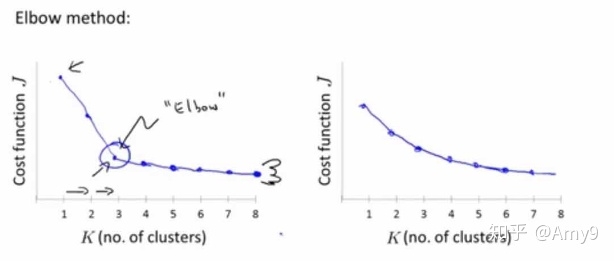
• 用“Elbow Method”(肘部法则)来选择K的数量；
  需要画图（横轴聚类的数量，纵轴损失函数），选择曲线明显的拐点作为K；
  但也会存在没有清晰的拐点，无法选出K的数；

• 根据后续目标来选择聚类数目；
  比如哪种衬衫尺码会更好的满足我的顾客。
  衬衫的尺码数k=3（S M L）还是k=5（XS S M L XL），选哪个会让顾客更满意（这是目标）；

补充

如果没有数据，也可以通过python现有库模拟产生数据，代码如下

from 

用模拟生成的数据替换上面代码中的x和k，则调算法包和用原理实现的运行效果分别如下

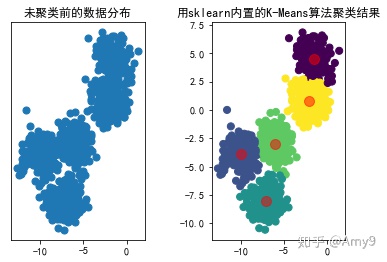
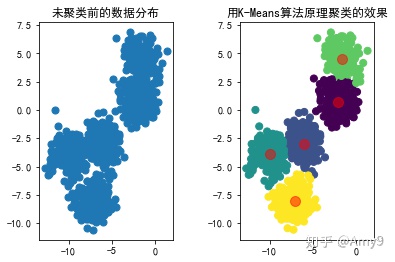
总结

用封装好的算法和用原理实现的算法相比，从时间上来看，封装好的算法要比按原理实现的速度快，后续探索到其他方面再补充。