Leetcode 4.2

回溯

1.全排列

全排列
回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> tmp;

    vector<vector<int>> permute(vector<int>& nums) {
        vector<bool> used(nums.size(), false);
        dfs(nums, used);
        return ans;
    }

    void dfs(vector<int>& nums, vector<bool>& used) {
        if (tmp.size() == nums.size()) {
            ans.push_back(tmp);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {
            if (used[i] == true) continue;
            tmp.push_back(nums[i]);
            used[i] = true;
            dfs(nums, used);
            tmp.pop_back();
            used[i] = false;
        }
    }

};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

2.子集

子集

题解参考链接
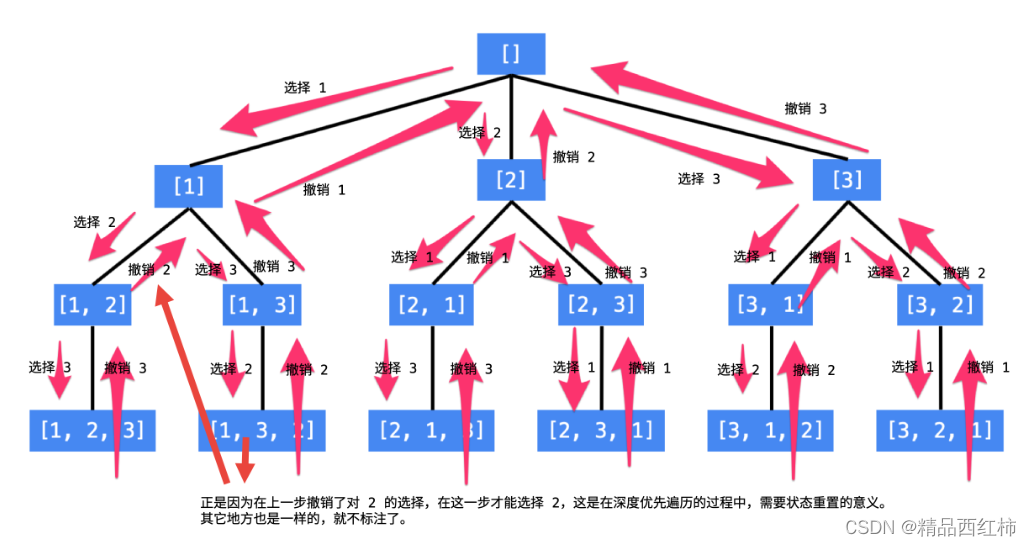
①递归树
观察上图可得，选择列表里的数，都是选择路径(红色框)后面的数，比如[1]这条路径，他后面的选择列表只有 “2、3”，[2] 这条路径后面只有 “3” 这个选择，那么这个时候，就应该 使用一个参数 start，来标识当前的选择列表的起始位置。也就是标识每一层的状态，因此被形象的称为 “状态变量”.

//nums为题目中的给的数组
//path为路径结果，要把每一条 path 加入结果集
void backtrack(vector<int>nums,vector<int>&path,int start)
1
2
3

②找结束条件
此题非常特殊，所有路径都应该加入结果集，所以不存在结束条件。或者说当 start 参数越过数组边界的时候，程序就自己跳过下一层递归了，因此不需要手写结束条件,直接加入结果集

**res为结果集，是全局变量vector<vector<int>>res,到时候要返回的
res.push_back(path);//把每一条路径加入结果集
1
2

③找选择列表
在①中已经提到过了，子集问题的选择列表，是上一条选择路径之后的数,即

for(int i=start;i<nums.size();i++)
1

④判断是否需要剪枝
从递归树中看到，路径没有重复的，也没有不符合条件的，所以不需要剪枝

⑤做出选择(即for 循环里面的)

void backtrack(vector<int>nums,vector<int>&path,int start)
{
    for(int i=start;i<nums.size();i++)
    {
        path.push_back(nums[i]);//做出选择
        backtrack(nums,path,i+1);//递归进入下一层，注意i+1，标识下一个选择列表的开始位置，最重要的一步
    }
}
1
2
3
4
5
6
7
8

⑤撤销选择
整体的 backtrack 函数如下

C++
void backtrack(vector<int>nums,vector<int>&path,int start)
{
    res.push_back(path);
    for(int i=start;i<nums.size();i++)
    {
        path.push_back(nums[i]);//做出选择
        backtrack(nums,path,i+1);//递归进入下一层，注意i+1，标识下一个选择列表的开始位置，最重要的一步
        path.pop_back();//撤销选择
    }
}
1
2
3
4
5
6
7
8
9
10
11

代码

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> tmp;
    vector<vector<int>> subsets(vector<int>& nums) {
        dfs(nums, 0);
        return ans;
    }
    
    void dfs(vector<int>& nums, int start) {
        ans.push_back(tmp);
        for (int i = start; i < nums.size(); i++) {
            tmp.push_back(nums[i]);
            dfs(nums, i + 1);
            tmp.pop_back();
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3.组合总和

组合总和

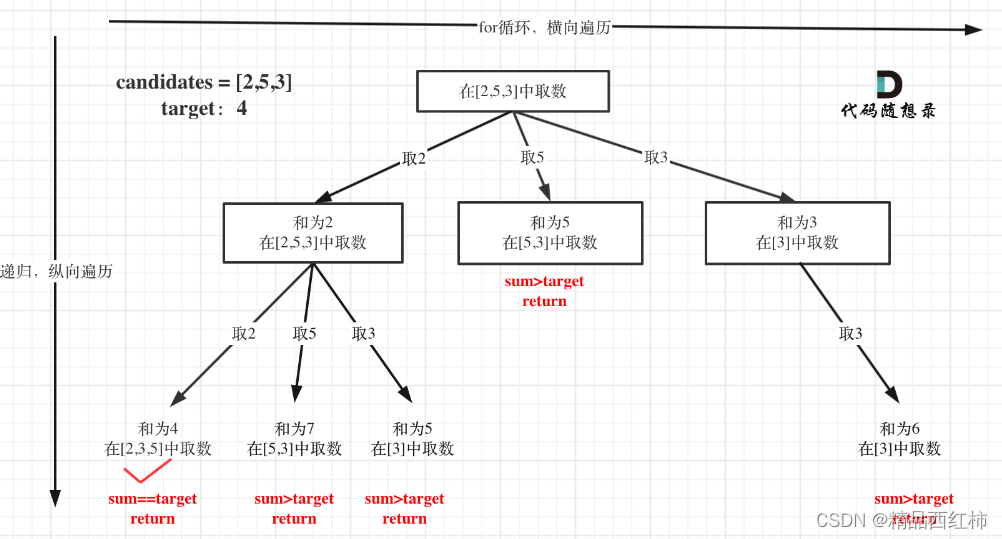
这里依然是定义两个全局变量，二维数组ans存放结果集，数组tmp存放符合条件的结果。（这两个变量可以作为函数参数传入）

首先是题目中给出的参数，集合candidates, 和目标值target。

本题还需要start Index来控制for循环的起始位置。

• 递归终止条件

从叶子节点可以清晰看到，终止只有两种情况，sum大于target和sum等于target。
sum等于target的时候，需要收集结果。

• 单层搜索的逻辑

单层for循环依然是从startIndex开始，搜索candidates集合。

注意本题元素为可重复选取的。

如何重复选取呢，看代码，注释部分：

for (int i = startIndex; i < candidates.size(); i++) {
    sum += candidates[i];
    path.push_back(candidates[i]);
    backtracking(candidates, target, sum, i); // 关键点:不用i+1了，表示可以重复读取当前的数
    sum -= candidates[i];   // 回溯
    path.pop_back();        // 回溯
}
1
2
3
4
5
6
7

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> tmp;
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        dfs(candidates, target, 0, 0);
        return ans;
    }
    void dfs(vector<int>& candidates, int target, int sum, int start) {
        if (target < sum) {
            return;
        }
        if (target == sum) {
            ans.push_back(tmp);
            return;
        }
        for (int i = start; i < candidates.size(); i++) {
            tmp.push_back(candidates[i]);
            sum += candidates[i];
            dfs(candidates, target, sum, i); //i不需要+1，因为可以重复取数
            tmp.pop_back();
            sum -= candidates[i];
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25