热门标签
热门文章
- 1深度学习(11)之Anchor-Free详解
- 2算法训练营第六十九天 | 并查集理论基础、寻找存在的路径、冗余连接、冗余连接II_卡码网
- 3Git常用命令大全_git rename
- 4弹出框 custombox.min.js 使用时候由于滚动条隐藏造成网页抖动变形的解决办法
- 5【前端系列】20种 Button 样式_前端按钮
- 6uniapp:完成商品分类页面(scroll-view),左侧导航,右侧商品_uniapp左侧导航右侧内容
- 7深度学习实战—基于TensorFlow 2.0的人工智能开发应用_深度学习实战:基于tensorflow
- 8QT网络编程之实现TCP客户端和服务端_qt tcp客户端
- 9哈工大(HIT)计算机网络 翻转课堂 实验 mooc答案 总结_哈工大计网mooc答案
- 10Stable Diffusion学习笔记_马尔科夫链的反向过程是
当前位置: article > 正文
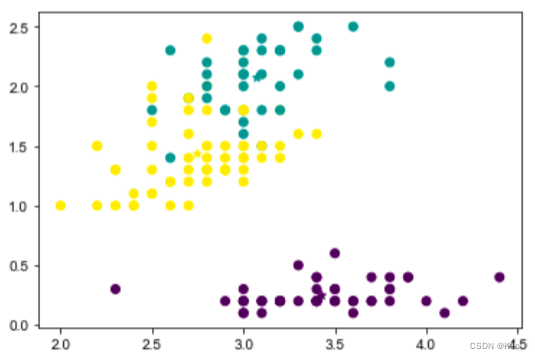
python数据挖掘——聚类_python 数组 聚类
作者:盐析白兔 | 2024-06-14 22:52:50
赞
踩
python 数组 聚类
划分聚类
Kmeans
原理
(1)任意选择k个对象作为初始的簇中心;(2)根据距离(欧式距离)中心最近原则,将其他对象分配到相应类中;(3) 更新簇的质心,即重新计算每个簇中对象的平均值;(4) 重新分配所有对象,直到质心不再发生变化
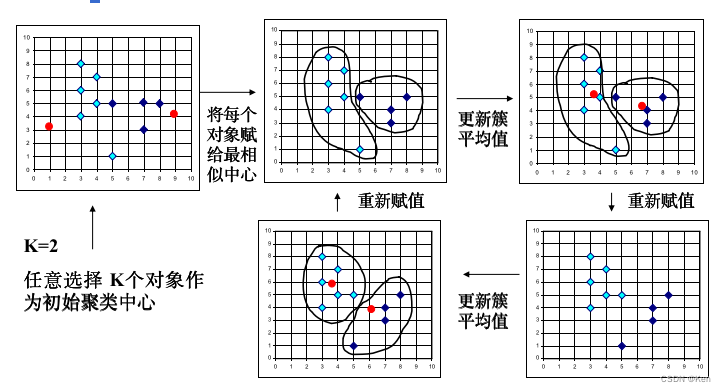
调包实现
- import time
- import pandas as pd
- from sklearn import preprocessing
-
- data = pd.read_csv("/.../iris.csv")
- iris = data.iloc[:,:4] # 获取iris数据
- target = data.iloc[:,4:] # 单独存放species属性
-
- # 预处理
- # 将species转换成数字
- class_encoder = preprocessing.LabelEncoder()
- target['species'] = class_encoder.fit_transform(target['species'].values)
- # K-means
- from sklearn.cluster import KMeans
- # 将数据聚为3类
- kms = KMeans(n_clusters = 3)
- # 训练数据
- kms.fit(iris)
- # 预测结果
- kms_label = kms.labels_
- kms_label = pd.DataFrame(kms_label,columns=["聚类结果"])
- kms_iris = iris.copy()
- kms_iris["聚类结果"] = kms_label
- kms_iris

参数调优
- # 肘方法确定参数
- SSE_list = []
- for n in range(1,10):
- kms = KMeans(n_clusters=n)
- kms.fit(iris)
- SSE_list.append(kms.inertia_)
-
- plt.xlabel = "n_clusters"
- plt.ylabel = "SSE"
- plt.plot(range(1,10),SSE_list,"o-")
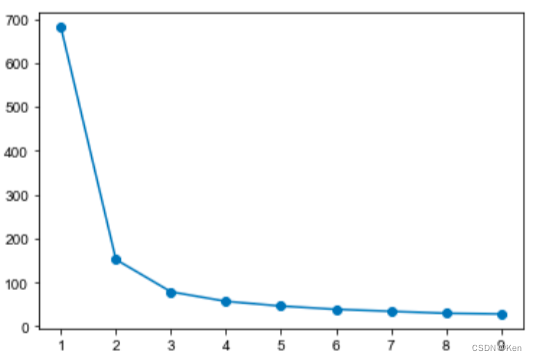
结果可视化
- kms_cc = pd.DataFrame(kms.cluster_centers_,
- index=[0,1,2],
- columns=['sepal_length','sepal_width','petal_length','petal_width'])
- kms_iris = pd.concat([kms_iris,kms_cc])
- fig = plt.figure()
- ax = fig.add_subplot()
- ax.scatter(x=kms_iris.iloc[:150,1:2],y=kms_iris.iloc[:150,3:4],c=kms.labels_,label=[1,2,0])
- ax.scatter(x=kms_iris.iloc[150:,1:2],y=kms_iris.iloc[150:,3:4],c=[0,1,2],marker='*')
- plt.show()
自己实现

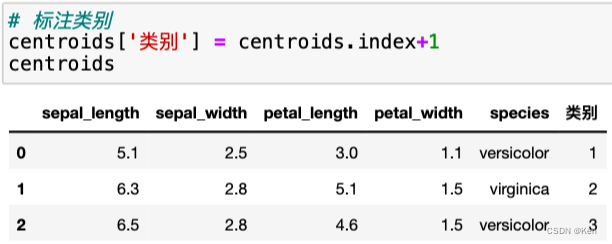


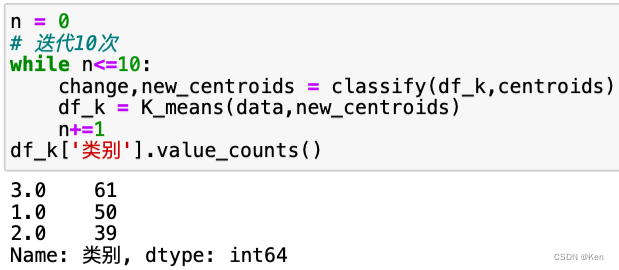

K-Medoids
不采用簇中对象的平均值作为参照点, 而是选用簇中位置最中心的对象, 即中心点作为参照点
PAM算法
反复地用非代表对象替代代表对象,以改进聚类的质量
CLARA算法
随机地抽取多个样本,针对每一个样本寻找代表对象medoids,并进行全部数据对象的聚类,然后从中选择质量最好的聚类结果作为最终结果,并分配其余对象。
层次聚类
分裂型层次聚类法
分割最不相似的两个部分,从所有的对象归属在唯一的一个簇中开始,逐层向下分解,直到每一个对象形成一个簇。
凝聚型AGNES
(1)首先将每一个对象独立地作为一个簇。 (2)然后根据各个簇之间的相似程度(距离)逐层向上聚结,形成越来越大的簇。 (3)最终形成包含全部对象的唯一的一个簇,也可以在满足一定的聚结终止条件时终止聚结。
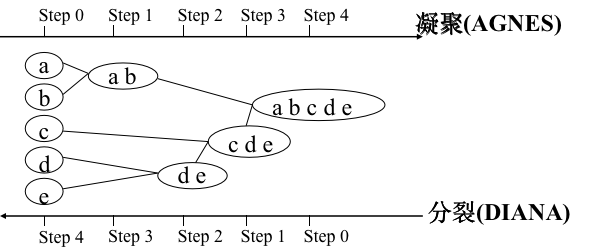
代码实现
- # AGNES聚类
- from sklearn.cluster import AgglomerativeClustering
- # 将数据聚为3类
- ac = AgglomerativeClustering(linkage='complete',n_clusters=3)
- # 训练数据
- ac.fit(iris)
- # 得到结果
- ac_label = ac.labels_
- ac_label = pd.DataFrame(ac_label,columns=["聚类结果"])
- ac_iris = iris.copy()
- ac_iris["聚类结果"] = ac_label
- # 数据匹配
- ac_iris["聚类结果"].loc[ac_iris["聚类结果"]==2] = 'x'
- ac_iris["聚类结果"].loc[ac_iris["聚类结果"]==0] = 2
- ac_iris["聚类结果"].loc[ac_iris["聚类结果"]==1] = 0
- ac_iris["聚类结果"].loc[ac_iris["聚类结果"]=='x'] = 1
- ac_iris

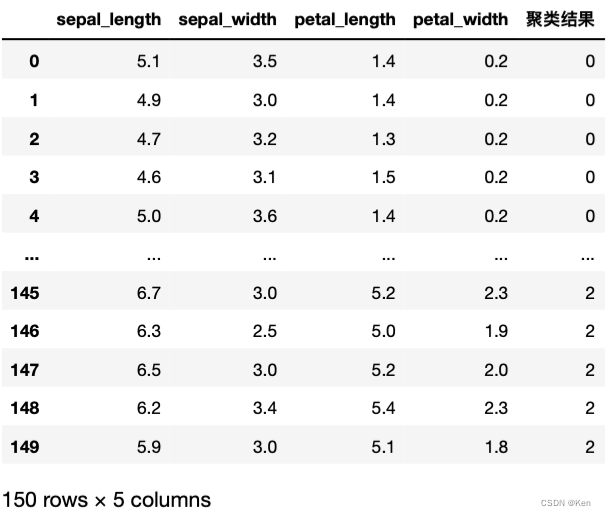
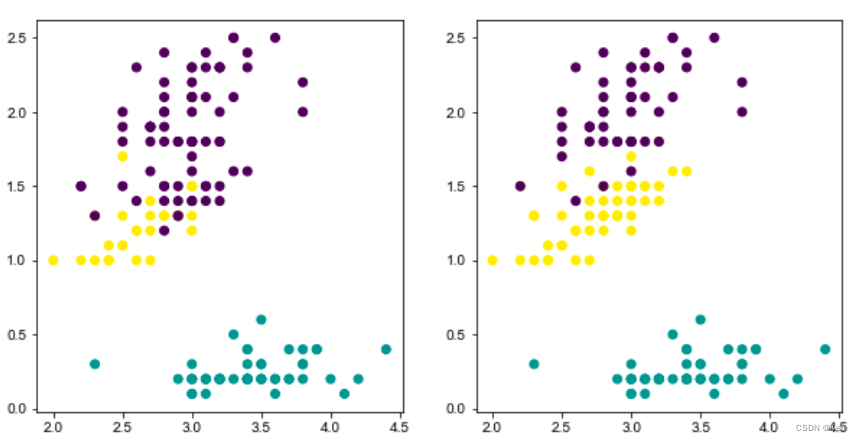
层次聚类树
- # 层次聚类树
- from scipy.cluster import hierarchy
- plt.figure(figsize=(15,5))
- # 生成聚类树
- Z = hierarchy.linkage(ac_iris,method='weighted',metric='euclidean')
- hierarchy.dendrogram(Z)
- plt.show()

BIRCH算法
假设在给定的一个簇中,有n个m维的数据点,
该簇的聚类特征向量CF = (N, LS, SS):(1) N是该类中的数据点数目;(2) LS是该n个数据点的线性和,即 ;(3) SS是该n个数据点的平方和,即
密度聚类
DBSCAN
关键概念:核心对象、直接密度可达、密度可达、密度相连、簇与噪声
调包实现
- # DBSCAN
- from sklearn.cluster import DBSCAN
- # 设置邻域半径为0.81,MinPts为10
- db = DBSCAN(eps=0.81, min_samples=10)
- # 训练数据
- db.fit(iris)
- # 得到结果
- db_label = db.labels_
- db_label = pd.DataFrame(db_label,columns=["聚类结果"])
- db_iris = iris.copy()
- db_iris["聚类结果"] = db_label
- db_iris
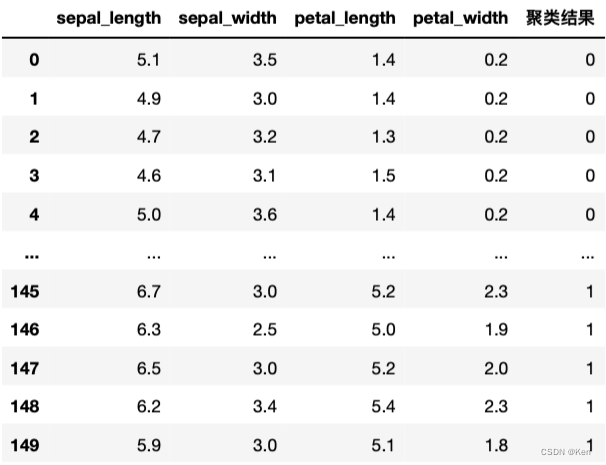
由于聚类是无监督学习,聚类结果可能与本身的标签不匹配,所以还需要做数据匹配。下图还没有做数据匹配,可以通过颜色看出聚类结果与本身标签并不对应。

参数调优
- # 确定最佳参数
- db_list = []
- for each_eps in np.arange(0.01,10,0.10):
- for each_minpts in range(5,11):
- db = DBSCAN(eps=each_eps,min_samples=each_minpts)
- # 训练模型
- db.fit(iris)
- db_label = db.labels_
- db_label = pd.DataFrame(db_label,columns=["聚类结果"])
- n = pd.DataFrame(db.labels_).value_counts().size-1 # 簇数
- db_iris = iris.copy()
- db_iris["聚类结果"] = db_label
- try:
- score = silhouette_score(db_iris,db.labels_) # 轮廓系数
- db_list.append({'eps':each_eps,'min_samples':each_minpts,
- 'n_clusters':n,'轮廓系数':score})
- except:
- continue

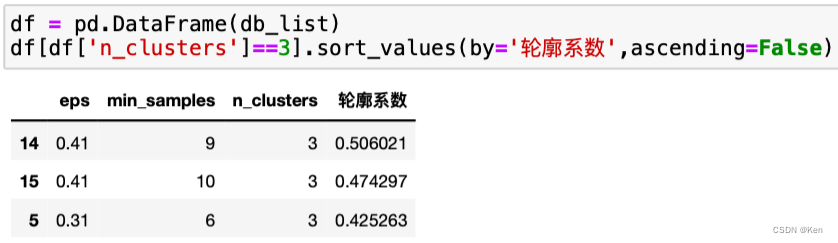
所以设置邻域半径为0.81,MinPts为10
自己实现(待完善)
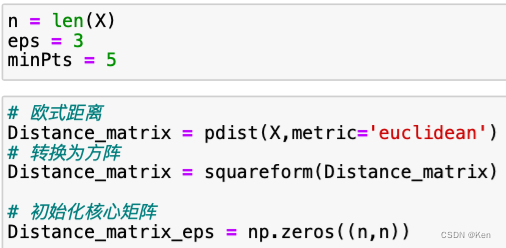

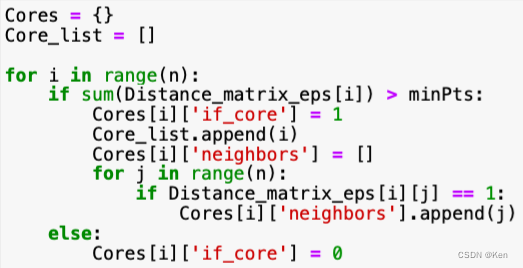
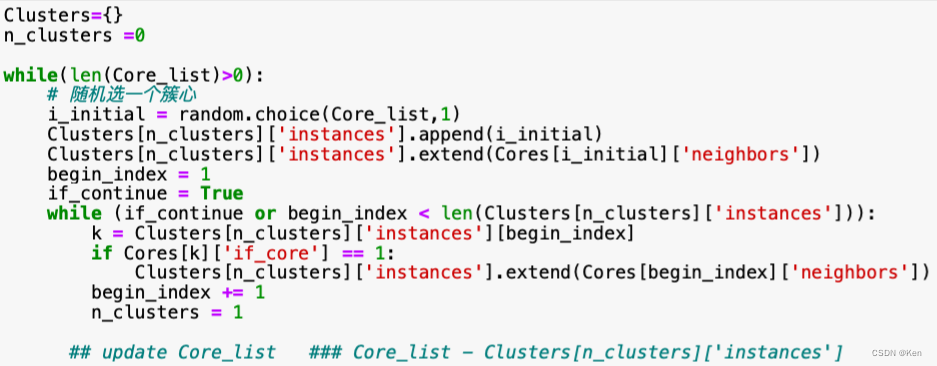
OPTICS算法
优先选择最小的值密度可达的对象, 以便高密度的聚类能被首先完成
聚类评价
下图是已经做过数据匹配之后的结果,p4是原分类结果

兰德系数
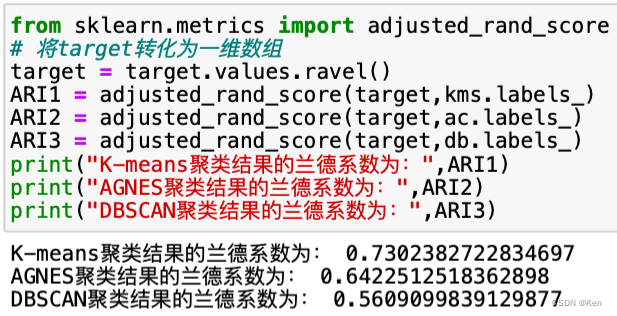
FMI

DBI 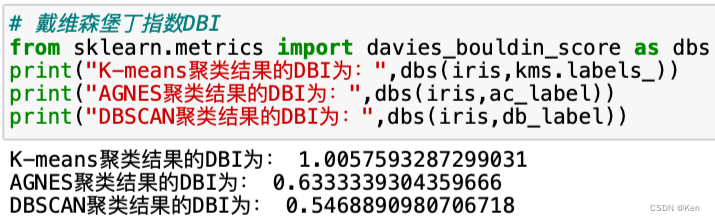
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/盐析白兔/article/detail/719940
推荐阅读
相关标签