SIFT算法提取关键点_sift手工选择关键点

这里只是用了一层图像
原理框图：

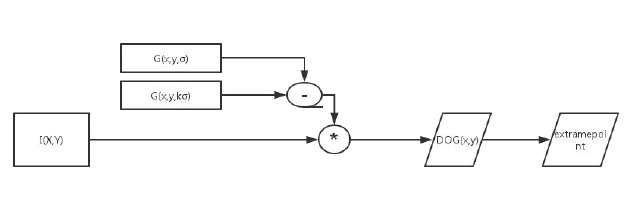
而为了简化计算，我们不直接求二维的高斯卷积核，而是将它变成两个一维的卷积核，原理如下图

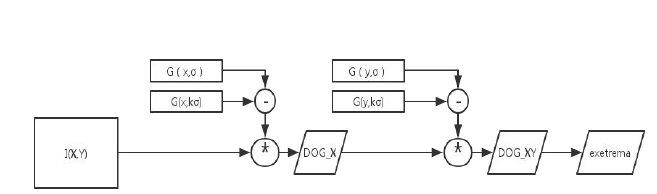
1. 构建图像尺度空间(图像的高斯金字塔)
所谓高斯金字塔，是指假设一个金字塔型的结构，金字塔的第一层为原图像，然后将图像做一次高斯平滑（高斯卷积或者高斯模糊），而在高斯平滑里有一个参数σ，然后将σ乘以一个系数k之后得到的值作为新的平滑因子来平滑第二层作为第三层，重复多次，我们就可以得到一组高斯金字塔，而在本次实验中，我们只做到了第三层，即只对原图做了两次高斯平滑处理。
2. 获得DOG(Difference of Gaussian)金字塔
DOG是指高斯差分，是从高斯金字塔构造出来的。它的第一层是有高斯金字塔的第二层减去第一层，第二层是由高斯金字塔的第三层减去第二层，如此类推。
3. 定位极值点
由于关键点是由DOG空间的局部极值点组成的。所以为了定位极值点，我们需要将每一个像素点和它所有的相邻像素点进行比较，看它是否比相邻像素点大或者小。这里我们使用每个像素和它的八邻域作比较，如果该像素是该区域内最大并且大于一定阀值的话，则为极大值点，相同地，如果该像素是该区域最小并且小于一定阀值时，则视为极小值点。
代码如下：

clear all
close all
% 读取图片
I = imread('TENNIS.png');
% 将图片转为灰度图
F = rgb2gray(I);
subplot(221):imshow(F):title('原图');
% 分别求出高斯尺度变换
GX_k = fspecial('gaussian',[5 1],0.8*sqrt(2))
GX = fspecial('gaussian',[5 1],0.8);
% 求在x方向的高斯卷积核
DOG_X = conv2(GX,F) - conv2(GX_k,F);
subplot(222):imshow(DOG_X):title('DOG X');    % DOG_X
% 分别求出高斯尺度变换
GY_k = fspecial('gaussian',[1 5],0.8*sqrt(2));
GY = fspecial('gaussian',[1 5],0.8);
% % 求xy方向的高斯卷积核，得到图片F的DOG图
DOG_XY = conv2(GY,DOG_X) - conv2(GY_k,DOG_X);
subplot(223):imshow(DOG_XY):title('DOG XY');   % DOG_XY
% 定位极值点，0.15为阈值
[m n] = size(DOG_XY);
extream = zeros(m,n);
for i = 1:m;
    for j = 1:n;
        if i==1||j==1||i==m||j==n
            if i==1&&j==1||i==1&&j==n||i==m&&j==1||i==m&&j==m

            else
            end
        else
             a = [DOG_XY(i-1,j-1),DOG_XY(i-1,j),DOG_XY(i-1,j+1),DOG_XY(i,j-1),DOG_XY(i,j),DOG_XY(i,j+1),DOG_XY(i+1,j-1),DOG_XY(i+1,j),DOG_XY(i+1,j+1)];
        end
             % 极大值点
             if DOG_XY(i,j) == max(a) && DOG_XY(i,j)>=0.15
                extream(i,j) = 1;
             end
            % 极小值点
            if DOG_XY(i,j) == min(a) && DOG_XY(i,j)<=-0.15
                extream(i,j) = -1;
            end
    end
end
% 显示极值点 
 subplot(224):imshow(I):title('Extream Points');
 hold on;
 [a b] = size(extream);
 for i = 2:a-1
     for j = 2:b-1
         if extream(i,j) == 1
             line('xdata',[j-1,j+1],'ydata',[i-1,i-1],'color','red');
             line('xdata',[j-1,j+1],'ydata',[i+1,i+1],'color','red');
             line('xdata',[j-1,j-1],'ydata',[i-1,i+1],'color','red');
             line('xdata',[j+1,j+1],'ydata',[i-1,i+1],'color','red');
         end
         if extream(i,j) == -1
             line('xdata',[j-1,j+1],'ydata',[i-1,i-1],'color','green');
             line('xdata',[j-1,j+1],'ydata',[i+1,i+1],'color','green');
             line('xdata',[j-1,j-1],'ydata',[i-1,i+1],'color','green');
             line('xdata',[j+1,j+1],'ydata',[i-1,i+1],'color','green');
         end
     end
 end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63