[论文分享] jTrans: Jump-Aware Transformer for Binary Code Similarity

jTrans: Jump-Aware Transformer for Binary Code Similarity [ISSTA 2022]

二进制代码相似性检测(Binary code similarity detection, BCSD)在漏洞检测、软件构件分析、逆向工程等领域具有重要应用。最近的研究表明，深度神经网络(DNNs)可以理解二进制代码的指令或控制流图(CFG)，并支持BCSD。本文提出一种新的基于transformer的方法，即jTrans，来学习二进制代码的表示。它是第一个将二进制代码的控制流信息嵌入到基于transformer的语言模型中的解决方案，通过使用所分析的二进制代码的新的跳跃感知表示和新设计的预训练任务。此外，我们向社区发布了一个新创建的大型二进制数据集BinaryCorp，这是迄今为止最多样化的。评估结果表明，jTrans在这个更具挑战性的数据集上比最先进的(SOTA)方法性能提高了30.5%(即从32.0%到62.5%)。在一个真实的已知漏洞搜索任务中，jTrans取得了比现有SOTA基线高2倍的召回率。

一句话：jTrans，对二进制代码的控制流信息结合到transformer的嵌入中

导论

在机器学习应用于该领域之前，传统的BCSD解决方案严重依赖二进制代码的特定特征，即函数的控制流图(CFGs)，它捕获程序的语法知识。BinDiff[64]、BinHunt[23]和iBinHunt[46]等解决方案采用图同构技术来计算两个函数CFGs的相似度。然而，这种方法既耗时又不稳定，因为CFGs可能根据编译器优化而改变。BinGo[5]和Esh[8]等研究通过计算CFG片段的相似度，对CFG变化具有更强的鲁棒性。然而，这些方法基于人工设计的特征，难以捕捉二进制代码的精确语义。因此，这些解决方案往往具有相对较低的精度。
随着机器学习技术的快速发展，目前大多数最先进的BCSD解决方案都是基于学习的。通常，这些解决方案将目标二进制代码(如函数)嵌入到向量中，并计算函数在向量空间中的相似度。一些解决方案，如Asm2Vec[14]和SAFE[43]，使用受自然语言处理(NLP)启发的语言模型来建模汇编语言(机器代码)。其他研究使用图神经网络(GNNs)来学习CFGs的表示并计算它们的相似性。一些研究结合了这两种方法，通过NLP技术学习基本块的表示，并通过GNN进一步处理CFG中的基本块特征，例如[44,62]。尽管性能有所提高，但现有方法有一些局限性。

通过在指令的每个跳转目标的标记嵌入和位置嵌入之间共享参数，修改Transformer来捕获控制流信息。首先利用无监督学习任务对jTrans进行预训练，以学习二进制函数的指令语义和控制流信息;接下来，对预训练的jTrans进行微调，以匹配语义相似的函数。请注意，我们的方法能够使用语言模型组合每个基本块的特征，而不依赖gnn遍历相应的CFG。
除了所提出的新方法，还提出了一个大型和多样化的数据集BinaryCorp，从ArchLinux的官方存储库[2]和Arch用户存储库(AUR)[3]中提取。新创建的数据集使我们能够缓解现有数据集的过拟合和多样性缺乏。我们自动地从包含大多数流行开源软件的仓库中收集所有的c/c++项目，并使用不同的编译器优化来构建它们以生成不同的二进制文件。据我们所知，我们的数据集是迄今为止用于BCSD任务的最大、最多样化的二进制程序数据集。

Contributions

(1) 本文提出了一种新的基于Transformer的跳变感知模型jTrans，这是第一个将控制流信息嵌入Transformer的解决方案。该方法能够学习二进制代码表示，并支持真实世界的BCSD。我们在https://github.com/vul337/jTrans上发布jTrans的代码。
(2) 本文创建了一个新的大规模、结构良好和多样化的数据集BinaryCorp，用于BCSD的任务。据我们所知，BinaryCorp是迄今为止最多样化的，它可以显著减轻以前基准的过拟合问题。
(3) 进行了广泛的实验，表明该模型可以明显优于SOTA方法。

PROBLEM DEFINITION

BCSD是计算两个二元函数相似度的基本任务。它可以用于中讨论的三种类型的场景，包括(1)一对一(OO)，其中返回一个源函数与一个目标函数的相似度分数;(2)一对多(OM)，其中目标函数池将根据它们与一个源函数的相似度得分进行排序;(3)多对多(MM)，函数池将根据相似度分成组。
在不失一般性的情况下，本文关注OM任务。注意，我们可以通过将目标函数的大小设置为1来将OM问题简化为OO问题。我们也可以将OM问题扩展到MM，将池中的每个函数作为源函数，同时求解多个OM问题。为了使演示更加清晰，我们对这些问题进行了如下的正式定义:

Related Works

基于学习的BCSD研究受到了自然语言处理(NLP)最新发展的启发，该发展使用称为嵌入的实值向量来编码单词和句子的语义信息。在这些技术的基础上，之前的研究将深度学习方法应用于二进制相似性检测。这些研究的共同思想是将二进制函数嵌入到数值向量中，然后使用向量距离来近似不同二进制函数之间的相似性。如图2所示，这些方法使用深度学习训练算法，使逻辑上相似的二进制函数的向量距离更近。

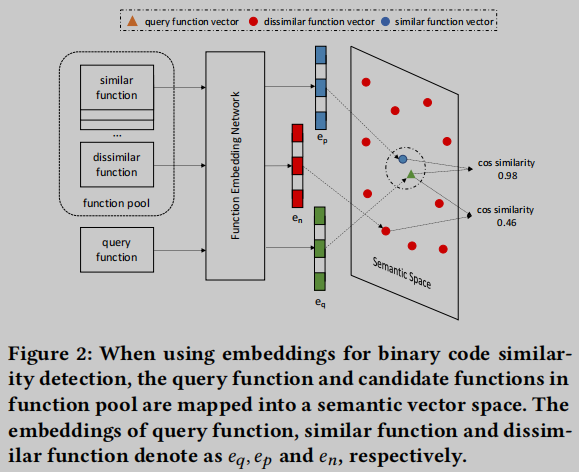
大多数基于学习的方法使用孪生网络[6]，它需要训练等价的二元函数的基本真值映射。