- 1去哪里找抖音短视频素材?告诉大家几个抖音短视频素材下载资源_抖音资源哪里找
- 2Linux权限有哪些?500代表什么意思?_权限500啥意思
- 3软件测试面试题及答案_软件测试上机考试面试
- 4【机器学习入门】拥抱人工智能,从机器学习开始
- 5微信小程序使用ColorUI组件库_微信小程序只引用部分colorui组件
- 6使用Typecho搭建个人博客网站,并内网穿透实现公网访问
- 7算法沉淀——BFS 解决拓扑排序(leetcode真题剖析)_bfs拓扑排序
- 8pytorch实现word embedding :torch.nn.Embedding_pytorch embedding python 实现
- 9JVM笔记_java 虚拟机的类型
- 10【OpenVINO】基于 OpenVINO Python API 部署 RT-DETR 模型_openvino 的github链接
Leetcode - 周赛395
赞
踩
目录
一,3131. 找出与数组相加的整数 I

本题本质就是求两个数组最小值的差。
代码如下:
- class Solution {
- public int addedInteger(int[] nums1, int[] nums2) {
- Arrays.sort(nums1);
- Arrays.sort(nums2);
- return nums2[0]-nums1[0];
- }
- }
二,3132. 找出与数组相加的整数 II

本题要先将数组排序,然后暴力枚举移除的两个数,然后判断两个数组对应下标的差值是否相同,如果全部相同,就直接返回差值。题目中还要求差值必须时最小的,这点不用担心,因为上述的枚举实际上就是按照差值从小到大的顺序,所以第一个满足条件的一定是最小的
代码如下:
- class Solution {
- public int minimumAddedInteger(int[] nums1, int[] nums2) {
- Arrays.sort(nums1);
- Arrays.sort(nums2);
- for(int i=0; i<nums1.length; i++){
- for(int j=i+1; j<nums1.length; j++){
- int ans = Integer.MAX_VALUE;
- int idx = 0;
- for(int k=0; k<nums1.length; k++){
- if(k!=i && k!=j){
- if(ans==Integer.MAX_VALUE || ans==nums2[idx]-nums1[k]){
- ans = nums2[idx]-nums1[k];
- idx++;
- }else{
- break;
- }
- }
- }
- if(idx == nums2.length) return ans;
- }
- }
- return -1;
- }
- }

除了上述做法,还有一种更简单的做法,题目中说了只删除两个数,也就是说排完序后,其实差值只有这三种情况:
- nums2[0] - nums1[0]
- nums2[0] - nums1[1]
- nums2[0] - nums1[2]
然后依次判断这三中情况是否符合条件,如果符合就返回答案,题目还要求差值必须是最小的,所以要反过来遍历。
代码如下:
- class Solution {
- public int minimumAddedInteger(int[] nums1, int[] nums2) {
- Arrays.sort(nums1);
- Arrays.sort(nums2);
- for(int i=2; i>=0; i--){
- int ans = nums2[0] - nums1[i];
- int idx = 0;
- for(int j=i; j<nums1.length; j++){
- if(ans == nums2[idx]-nums1[j]){
- idx++;
- if(idx == nums2.length)
- return ans;
- }
- }
- }
- return -1;
- }
- }

三,3133. 数组最后一个元素的最小值

本题是一道二进制运算题,由&的性质可知:
- &的数越多,&的值就越小
- &的值一定小于等于所有参与&运算的数中的最小值
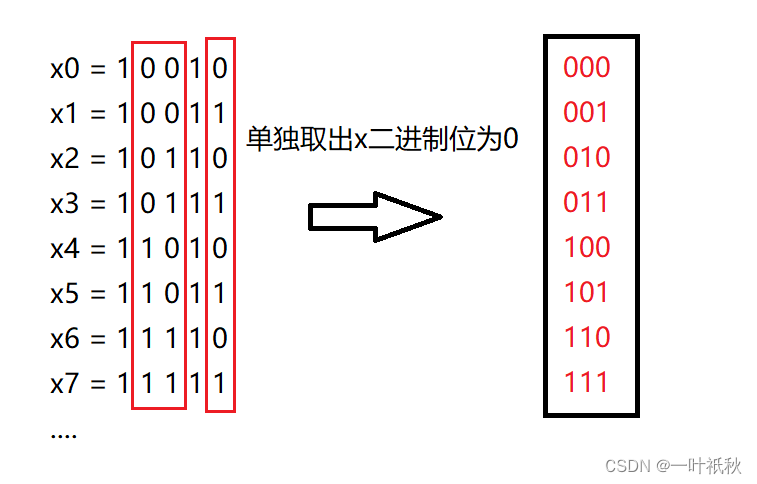
所以nums中第一个元素一定是x,那剩下的数该如何确定呢?我们知道1&0=0,要想使得nums数组的&值不变,只能改变x二进制位为0的部分(因为0&0=0,0&1=0,不会对&值产生影响),所以就可以去除x二进制位为1的部分,问题就变成了,将剩下的0如何变化,可以得到第n-1小的数,这不就是 001,010,011,100.....也就是说,我们只要将n-1的二进制位全部插入到x二进制位为0的位置就得到了答案。
- class Solution {
- public long minEnd(int n, int x) {
- n -= 1;
- long ans = x;
- int i = 0, j = 0;
- while(n>>i > 0){
- if((ans>>j&1)==0){//判断x的第j位二进制位是否为0
- ans |= (long)(n>>i&1)<<j;
- i++;
- }
- j++;
- }
- return ans;
- }
- }
优化做法:
- class Solution {
- public long minEnd(int n, int x) {
- n -= 1;
- long ans = x;
- int j = 0;
- long t = ~x;
- while(n>>j > 0){
- long lb = t&-t;//得到最低位的1
- ans |= (long)(n>>j&1)*lb;
- j++;
- t ^= lb;
- }
- return ans;
- }
- }
四,3134. 找出唯一性数组的中位数

二分答案 + 滑窗
题目问中位数,而中位数就是第n/2小的数,所以可以直接想到二分,二分需要有单调性,而
题目中说由distinct(nums[i...j)组成的distinct数组是递增数组,所以它具有单调性,就可以使用二分。接下来要解决的就是check方法如何实现。
我们知道满足check方法的条件就是在dis数组中<=mid的数的数量要>=((n+1)*n/2+1)/2,那么如何计算distinct数组中<=mid的数的数量呢,答案是滑窗:使用map不断的统计每个数出现的次数,如果map.size() > mid,就需要收缩窗口,cnt += r-l+1,不断的重复上述过程。
代码如下:
- class Solution {
- public int medianOfUniquenessArray(int[] nums) {
- Set<Integer> set = new HashSet<>();
- for(int x : nums)
- set.add(x);
- int l = 1, r = set.size();
- while(l <= r){
- int mid = (l + r) / 2;
- if(check(mid, nums)){
- r = mid - 1;
- }else{
- l = mid + 1;
- }
- }
- return r + 1;
- }
- boolean check(int k, int[] nums){
- Map<Integer, Integer> map = new HashMap<>();
- long cnt = 0;
- int n = nums.length;
- for(int l=0,r=0; r<n; r++){
- map.merge(nums[r], 1, Integer::sum);
- while(map.size() > k){
- if(map.merge(nums[l], -1, Integer::sum)==0)
- map.remove(nums[l]);
- l++;
- }
- cnt += r-l+1;
- }
- return cnt >= ((long)(n+1)*n/2+1)/2;
- }
- }