1.Leetcode刷题之数组篇_数组值和leetcode

题目分析与刷题记录

刷题顺序参考： 有没有人一起从零开始刷力扣
纯小白，有错误欢迎指正讨论，谢谢！

一、数组的遍历

414.第三大的数

给你一个非空数组，返回此数组中第三大的数。如果不存在，则返回数组中最大的数。
1

解法1： 维护一个有序数组，可以理解成有序的队列。遍历数组nums，使用insert插入有序数组，元素会自动排序、摆放。当有序数组超过3个元素时，使用erase删除最小的元素。最后判断有序数组元素个数是否小于3，小于则返回最大值，否则返回最大值。
代码：

class Solution {
public:
    int thirdMax(vector<int>& nums) {

    // 维护一个有序数组，进行删减操作
    set<int> s;
    for(int i = 0; i < nums.size(); i++)
    {
        s.insert(nums[i]);
        if(s.size() > 3)  s.erase(*s.begin());
    }
    return s.size() == 3 ? *s.begin() : *s.rbegin(); 
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

思考：
学习新建有序数组、及插入和删除元素方法，注意begin()、rbegin()和rend()的区别。

set<int> s; //创建有序数组s
s.insert(A)； //插入元素A
s.erase(B)； //删除元素B
/* s.begin()、s.rbegin()、s.end()的区别*/
s = {0,1,2,3,4}
s.begin()指向的是第一个元素0；
s.rbegin()指向的是反向后的第一个元素，即最后一个元素4；
s.end()指向的是最后一个元素的下一个，*s.end()返回的是存储单元中的一个随机数。
1
2
3
4
5
6
7
8

解法2： 遍历数组的方式来找第三大的数，a,b,c三个值用来维护nums数组中的最大值、次小值和第三大的数。a,b,c类似数组，根据输入数组的元素对abc进行更新。考虑三种情况：①若遍历的数组值num大于a，则num变为最大值，最大值变为次小值，次小值变为第三大的数；②// 若遍历的数组值num小于a但大于b，则a仍为最大值，num变为次小值，b变为第三大的数；③// 若遍历的数组值num小于b但大于c，则a仍为最大值，b仍为次小值，num变为第三大的数
代码：

class Solution {
public:
    int thirdMax(vector<int>& nums) {
        long a = LONG_MIN, b = LONG_MIN, c = LONG_MIN;  // a,b,c三个值用来维护nums数组中的最大值、次小值和第三大的数
        for(long num : nums)
        {
            if(num > a)  // 若遍历的数组值num大于a，则num变为最大值，最大值变为次小值，次小值变为第三大的数
            {
                c = b; b = a; a = num;
            }
            else if(num < a && num > b) // 若遍历的数组值num小于a但大于b，则a仍为最大值，num变为次小值，b变为第三大的数
            {
                c = b; b = num;  
            }
            else if(num < b && num > c) // 若遍历的数组值num小于b但大于c，则a仍为最大值，b仍为次小值，num变为第三大的数
                c = num;
        }
        return c == LONG_MIN ? a : c;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

思考：
1.进行数组元素比较时，可以初始化为T_MIN，T表示LONG、INT等；
2.为了不对原数组的值造成改变，可以新建数组来进行维护。

628.三个数的最大乘积

给你一个整型数组 nums ，在数组中找出由三个数组成的最大乘积，并输出这个乘积。
1

分析： 分成三种情况进行讨论：①若数组元素都是正数，则所求值应为最大的三个整数的乘积；②若数组元素都是负数，则所求值也是最大的三个整数的乘积；③若数组元素有正有负，则所求值应为$max${最大的三个整数的乘积，最大值和最小的两个整数的乘积}。
解法1： 关键在于找出最大的三个整数和最小的两个整数。采用$sort$函数对数组进行递减排序即可。
代码：

class Solution {
public:
    int maximumProduct(vector<int>& nums) {
    // 先对数组进行排序
    sort(nums.begin(),nums.end(),greater<>());
    return max(nums[0]*nums[1]*nums[2],nums[0]*nums[nums.size()-2]*nums[nums.size()-1]);
    }
};
1
2
3
4
5
6
7
8

思考：
学习$sort$函数的使用，对数组进行排序。
解法2： 使用线性扫描的方式找到三个最大值和两个最小值，并返回三个数的最大乘积。线性扫描的思想就是考虑插入值在几个数中的位置，对几个数进行更新，例如有$a,b,c$三个值，且依次递减，新插入一个值$n$，若$n>a$，则最大值$a=n$，次大值$b=a$，第三大的值$c=b$，其他情况类似。注意：写程序时，顺序要反过来，先完成第三大的值的替换，再是次大值，最后才是最大值。
代码：

class Solution {
public:
    int maximumProduct(vector<int>& nums) {
        int maxa = INT_MIN, maxb = INT_MIN, maxc = INT_MIN; //最大的三个数的初始化，依次为最大值、次大值、第三大的数
        int mina = INT_MAX, minb = INT_MAX;   //最小的两个数的初始化，依次为最小值、次小值
        //线性扫描找最大值
        for(auto& num : nums){
            if(num > maxa){
                maxc = maxb; maxb = maxa; maxa = num;
            }
            else if(num > maxb){
                maxc = maxb; maxb = num;
            }
            else if(num > maxc){
                maxc = num;
            }
        }
        //线性扫描找最小值
        for(auto& num : nums){
            if(num < mina){
                minb = mina; mina = num;
            }
            else if(num < minb)  minb = num;
        }
    return max(maxa*maxb*maxc, maxa*mina*minb);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

思考：
理解线性扫描的实现过程，掌握数组维护、更新和删除等操作。

二、统计数组中的元素

645.错误的集合

集合 s 包含从 1 到 n 的整数。不幸的是，因为数据错误，导致集合里面某一个数字复制了成了集合里面的另外一个数字的值，导致集合 丢失了一个数字 并且 有一个数字重复 。给定一个数组 nums 代表了集合 S 发生错误后的结果。请你找出重复出现的整数，再找到丢失的整数，将它们以数组的形式返回。
1

分析： 分成两个步骤：寻找重复的整数和寻找丢失的整数。
解法1： 哈希表。统计哈希表中元素出现的数目，若为2，则对应的元素为重复的数；若为0，则对应的元素为缺少的数。
代码：

class Solution {
public:
    vector<int> findErrorNums(vector<int>& nums) {
        unordered_map<int,int> hmap;
        for(auto& num:nums){
            hmap[num]++;
            // 存储地址改变，每个元素对应一个存储地址。
        }
        int a = 0, b = 0;
        for(int i = 1; i <= nums.size(); i++){
            int cnt = hmap[i];
            if(cnt == 2)
                a = i;
            else if(cnt == 0)
                b = i;
        }
    return {a,b};
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

思考：
哈希表是在关联词和存储位置之间建立映射关系（不同对不同，相同对相同），比如将关键词组“西瓜、香蕉、苹果”对应到存储地址$hash[i]$，详见以下哈希表的操作：

unordered_map<S,T> hmap; //创建key为S类型，映射到hash中存储为T类型的哈希表
hmap[num]++; //将num数值作为hash的下标，将该位置的值＋1，返回来理解,hash[i]中的i就是原数组中的元素，hash[i]表示数组中该元素的个数；
hmap.count(num);//判断哈希表中是否有重复的元素num，若有返回1，无则返回0；
hmap.first;//表示对应的关键字S元素
hmap.second;//表示对应的T元素
1
2
3
4
5

解法2： 采用线性扫描和讨论的方式求解，重复的元素好求解，通过遍历即可，复杂之处在于寻找缺少的数。首先对数组进行排序，再分成两种情况：①若缺少的数在$1-n$之间，其中$n=nums.size()$，则必然存在相邻两个元素的差为2；②若缺少的数字为$n$，对应的判断条件是第一个元素不为1；若缺少的数字为$n$，对应的判断条件是最后一个元素等于$n$。
代码：

class Solution {
public:
    vector<int> findErrorNums(vector<int>& nums) {
        vector<int> outarr = {0,0};
        sort(nums.begin(),nums.end());
        // 找出重复的数字
        for(int i = 0; i < nums.size()-1; i++){
            if(nums[i] == nums[i+1]){
                outarr[0] = nums[i];break;
            }
        }
        // 找出丢失的数字
        for(int i = 0; i < nums.size()-1; i++){
            if(nums[i+1]-nums[i] == 2)
                outarr[1] = nums[i] + 1;
                else if(nums[0] != 1) outarr[1] = 1;
                    else if(nums[nums.size()-1] != nums.size()) 
                            outarr[1] = nums[nums.size()-1] + 1;
        }
        return outarr;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

思考：
数组排序在统计数组元素中应用广泛，掌握递增、递减两种排序。

697. 数组的度 **

给定一个非空且只包含非负数的整数数组 nums，数组的 度 的定义是指数组里任一元素出现频数的最大值。你的任务是在 nums 中找到与 nums 拥有相同大小的度的最短连续子数组，返回其长度。
1

分析： 可分成三个步骤：S1.计算数组nums的度；S2.寻找拥有相同度的数组，统计初始和终止元素的下标；S3.返回最短数组的长度。
解法： 哈希表。创建三个哈希表，分别用来维护起始元素位置、终止元素位置以及该元素对应的度。S1.用哈希表统计元素num出现的个数，不断更新较大值得数组nums的度。S2.先维护统计初始和终止元素的下标的两个数组，如果统计初始元素下标的数组$left$满足$left.count(nums[i])=0$，即该元素在数组中只有1个，将此作为起点，终点对应的下标数组$right$就是最终的nums数组对应的下标$i$。S3.在元素对应的度中寻找相同度对应的初始和终止元素的下标，计算数组长度并返回最小值。
代码：

class Solution {
public:
    int findShortestSubArray(vector<int>& nums){
        unordered_map<int,int> left,right,counter;
        int degree = 0;
        for(int i = 0; i < nums.size(); i++){
            if(!left.count(nums[i]))
                left[nums[i]] = i;   // 如果left中没有nums[i]元素，则记下下标i为数组的起始位置
            right[nums[i]] = i;  // right中更新nums[i]的最新值，对应数组的最后位置
            counter[nums[i]]++;
            degree = max(degree, counter[nums[i]]);   
        }
    int minlen = nums.size();
        for(auto& cnt : counter){
            if(cnt.second == degree)
                minlen = min(minlen, right[cnt.first] - left[cnt.first] + 1);
        }
    return minlen;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

思考：
巩固哈希表的使用，尤其是$hmap.count(nums[i])$、$hmap.first$、$hmap.second$的使用，以及$max$、$min$函数的使用。

448.找到所有数组中消失的数字

给你一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果。
1

分析： 直接使用哈希表，统计哈希表中的元素。
解法： 哈希表。哈希表$1:nums.size()$中计数为0对应的下标$i$就是所求的元素，$push\_back(i)$。
代码：

class Solution {
public:
    vector<int> findDisappearedNumbers(vector<int>& nums) {
        unordered_map<int,int> hmap;
        vector<int> res;
        for(auto& num : nums){
            hmap[num]++;
        }
        int n = nums.size();
        for(int i = 1; i <= n; i++){
            if(!hmap[i])
                res.push_back(i);
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

442.数组中重复的数据 **

给你一个长度为 n 的整数数组 nums ，其中 nums 的所有整数都在范围 [1, n] 内，且每个整数出现 一次 或 两次 。请你找出所有出现 两次 的整数，并以数组形式返回。你必须设计并实现一个时间复杂度为 O(n) 且仅使用常量额外空间的算法解决此问题。
1

分析： 统计数组元素的常见方法就是借助哈希表，但是哈希表的时间复杂度为$O(N)$，空间复杂度最多也是$O(N)$，不符合题意，但是注意到本题整数的范围为$1-N$，可以使用原地哈希，即将数组本身作为哈希表，不需要单独开闭空间了。
解法： 哈希表对应两个要素：关键字$(nums[i])$和存储地址$(\ast nums[index],index=abs(nums[i])-1)$，哈希表中计数方式为翻转计数，即将$nums[index]$正负翻转计数，如果$nums[index]＞0$，则对应$nums[i]=index+1$在数组中是第一次出现，若$nums[index]<0$，则说明是第二次出现，对应$nums[i]=index+1$就是所求的数。
代码：

class Solution {
public:
    vector<int> findDuplicates(vector<int>& nums) {
        vector<int> res;
        int n = nums.size();
        for(int i = 0; i < n; i++){
            int index = abs(nums[i]) - 1;
            if(nums[index] > 0)
                nums[index] *= (-1);
            else
                res.push_back(index + 1);
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

思考：
深度理解哈希表的两个要素，以及在统计数组中的重复元素的应用。

41.缺失的第一个正数

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
1

分析： 同上，考虑到空间复杂度，应该构造原地哈希表，其中重要的一点是将哈希表的下标（存储地址）和数组的值（key）对应起来。所求正数范围应该在1-n+1之间，分为1-n和n+1两种情况，所以可以将数组中的负数变为n+1。
解法： S1.将数组中不在1-n的数据全部变为n+1，n为数组元素个数。S2.数组中元素值取绝对值-1刚好在0-n-1中，可以作为哈希表的下标。S3.对于哈希表的key（原数组中在1-n之间的数），若出现，不管一次、两次，均打上负号的标记，用负的绝对值来表示。S4.从哈希表第一个元素（下标0）开始搜索第一个正数，增加计数器，若全部为负数，则说明所求最小正数应该为n+1。
代码：

class Solution {
public:
    int firstMissingPositive(vector<int>& nums) {
        int n = nums.size();
        // 建立原地哈希表
        for(auto& num : nums){
            if(num < 1)
            num = n+1;
        }
        for(int i = 0; i < n; ++i){
                int index = abs(nums[i])-1 ;
                if(index < n){
                    nums[index] = -abs(nums[index]);
            }
        }
        int cnt = 0;
        int res = 0;
        // 寻找没有出现的元素
        for(int j = 0; j < n; ++j){
            if(nums[j] > 0){
                res = j+1;
                break;
            }
            else
                ++cnt;
        }
        return cnt==n ? n+1: res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

思考：
制作原地哈希表时，首要考虑的是筛选“入组”的条件，以及如何打标记以尽量减少对原数组的干扰和避免原数组重复元素的干扰。

274.H指数

给你一个整数数组 citations ，其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。根据维基百科上 h 指数的定义：h 代表“高引用次数”，一名科研人员的 h指数是指他（她）的 （n 篇论文中）总共有 h 篇论文分别被引用了至少 h 次。且其余的 n - h 篇论文每篇被引用次数 不超过 h 次。如果 h 有多种可能的值，h 指数 是其中最大的那个。
1

分析： 对数组进行排序，从大到小排列，下标刚好h指数。
解法： 排序后，判断数组中的第i个元素和hindex的大小。
代码：

class Solution {
public:
    int hIndex(vector<int>& citations) {
        int n = citations.size();
        sort(citations.begin(),citations.end(),greater<>());
        int hindex = 1;
        vector<int> nums;
        for(int i = 0; i < n; ++i){
            if(citations[i] >= hindex) ++hindex;
            else
                break;
        }
        return hindex-1;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

思考：
巩固数组排序。

274.H指数

给你一个整数数组 citations ，其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。根据维基百科上 h 指数的定义：h 代表“高引用次数”，一名科研人员的 h指数是指他（她）的 （n 篇论文中）总共有 h 篇论文分别被引用了至少 h 次。且其余的 n - h 篇论文每篇被引用次数 不超过 h 次。如果 h 有多种可能的值，h 指数 是其中最大的那个。
1

分析： 对数组进行排序，从大到小排列，下标刚好h指数。
解法： 排序后，判断数组中的第i个元素和hindex的大小。
代码：

class Solution {
public:
    int hIndex(vector<int>& citations) {
        int n = citations.size();
        sort(citations.begin(),citations.end(),greater<>());
        int hindex = 1;
        vector<int> nums;
        for(int i = 0; i < n; ++i){
            if(citations[i] >= hindex) ++hindex;
            else
                break;
        }
        return hindex-1;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

思考：
巩固数组排序。

三、数组的改变、移动

453.最小操作次数使数组元素相等

给你一个长度为 n 的整数数组，每次操作将会使 n - 1 个元素增加 1 。返回让数组所有元素相等的最小操作次数。
1

分析： 反过来考虑，每次操作使数组中的$1$个元素减少$1$，返回让数组所有元素相等的最小操作数，对数组排序后，计算操作次数即可，如$[1,3,2]$，排序完后是$[1,2,3]$，第一步操作应该是变为$[1,2,2]$，需要$1$次；第二、三步应该是变为$[1,1,2]$、$[1,1,1]$，需要$[2-1]\ast (2)$次。考虑总体规律，将$[a,b,b,b\dots \dots ]$其中有$1$个$a$，$m$个$b$，且$b＞a$，变为$[a,a,a,a\dots \dots ]$，至少需要$(b-a)\ast m$次。
解法： 先对数组进行排序，按照分析中的规律，$nums[i+1]$和$nums[i]$之间的操作数应该为$(nums[i+1]-nums[i])\ast m$，其中$m$是$nums[i+1]$后面的元素个数，即$nums.sizes()-i-1$。
代码：

class Solution {
public:
    int minMoves(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        int cnt = 0;
        for(int i = 0; i < nums.size()-1; i++){
            cnt+=((nums[i+1]-nums[i])*(nums.size()-i-1));
        }
        return cnt;
    }
};
1
2
3
4
5
6
7
8
9
10
11

665.非递减数列 **

给你一个长度为 n 的整数数组 nums ，请你判断在 最多 改变 1 个元素的情况下，该数组能否变成一个非递减数列。我们是这样定义一个非递减数列的： 对于数组中任意的 i (0 <= i <= n-2)，总满足 nums[i] <= nums[i + 1]。
1

分析： 如果数列中存在两组相邻元素满足$nums[i]>nums[i+1]$，则肯定无法修改1个元素成非递减数列。但是对于3 4 2 3这样的数列，就容易造成错判，还需要瞻前顾后。当$nums[i]>nums[i+1]$时，还要判断$nums[i-1]$和$nums[i+1]$的关系，再对$nums[i+1]$进行放缩变为$nums[i]$，即保留最大值，以便后续数列实现非递减，所谓之顾后。而$nums[i]>nums[i+1]$为瞻前，两者一起限制了相邻三个元素的大小关系。
解法： 满足$nums[i]>nums[i+1]$进行计数，之后修改$nums[i-1]$和$nums[i+1]$。
代码：

class Solution {
public:
    bool checkPossibility(vector<int>& nums) {
        int n = nums.size();
        int cnt = 0;
        for(int i = 0; i < n-1; ++i){
            if(nums[i] > nums[i+1]){
                ++cnt;
                if(cnt > 1) return false;
                // 注意下面if要放在if(nums[i] > nums[i+1])之中
            if(i > 0 && nums[i-1] > nums[i+1]){
                nums[i+1] = nums[i];
            }
            }
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

283.移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。请注意 ，必须在不复制数组的情况下原地对数组进行操作。
1

分析： 主要有两个步骤，寻找0元素，和移动0元素。
解法1： 首先找到0元素，再从该位置开始往后面寻找首位非零元素，与该0元素交换值。缺点是挨个寻找，效率较低。
代码：

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int n = nums.size();
        int temp = 0;
        for(int i = 0; i < n; ++i){
            if(nums[i] == 0){
                for(int j = 1; j < n - i; ++j){
                    if(nums[i+j] != 0)
                    {
                        temp = nums[i+j];
                        nums[i+j] = nums[i];
                        nums[i] = temp;
                        break;
                    }
                }
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

四、二维数组及滚动数组

118.杨辉三角

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。在「杨辉三角」中，每个数是它左上方和右上方的数的和。
1

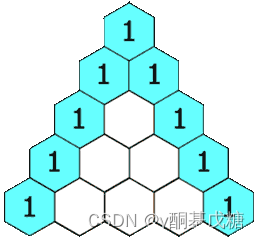
分析： 遍历数组，输出即可。
解法1： 遍历
代码：

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> yhtrigle(numRows);
        for(int i = 0; i < numRows; ++i){
            yhtrigle[i].resize(i+1);
            yhtrigle[i][0] = 1;
            yhtrigle[i][i] = 1;
            for(int j = 1; j < i; ++j){
                yhtrigle[i][j] = yhtrigle[i-1][j-1] + yhtrigle[i-1][j];
            }
        }
        return yhtrigle;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

思考：
注意数组的初始化，和resize(n)的使用——初始化大小为n的数组，全为0.

119.杨辉三角2

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。在「杨辉三角」中，每个数是它左上方和右上方的数的和。
1

分析： 遍历数组，输出即可。
解法1： 遍历
代码：

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<vector<int>> yhtrige(rowIndex+1);
        vector<int> res(rowIndex+1);
        for(int i = 0; i < rowIndex+1; ++i){
            yhtrige[i].resize(i+1);
            yhtrige[i][0] = yhtrige[i][i] = 1;
            for(int j = 1; j < i; ++j){
                yhtrige[i][j] = yhtrige[i-1][j-1] + yhtrige[i-1][j];
            }
        }
        for(int k = 0; k < rowIndex+1; ++k){
            res[k] = yhtrige[rowIndex][k];
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

661.图片平滑器 **

图像平滑器 是大小为 3 x 3 的过滤器，用于对图像的每个单元格平滑处理，平滑处理后单元格的值为该单元格的平均灰度。每个单元格的  平均灰度 定义为：该单元格自身及其周围的 8 个单元格的平均值，结果需向下取整。（即，需要计算蓝色平滑器中 9 个单元格的平均值）。如果一个单元格周围存在单元格缺失的情况，则计算平均灰度时不考虑缺失的单元格（即，需要计算红色平滑器中 4 个单元格的平均值）。
1

分析： 遍历数组，加减输出。
解法1： 扩展中心像素点的图窗，按3x3的来计算。
代码：

class Solution {
public:
    vector<vector<int>> imageSmoother(vector<vector<int>>& img) {
        int m = img.size();
        int n = img[0].size();
        vector<vector<int>> ret(m,vector<int>(n));
        for(int i = 0; i < m; ++i){
            for(int j = 0; j < n; ++j){
                int num = 0, sum = 0;
                for(int x = i - 1; x <= i + 1; ++x){
                    for(int y = j - 1; y <= j + 1; ++y){
                        if(x >= 0 && x < m && y >= 0 && y < n){
                            ++num;
                            sum += img[x][y];
                        }
                    }
                }
                ret[i][j] = sum/num;
            }
        }
        return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

思考：
注意使用vector构造二维数组，其中img是m*n的二维数组，则构造同样尺寸的二维数组代码为：

int m = img.size();
int n = img[0].size();
vector<vector<int>> ret(m,vector<int>(n));
1
2
3

598.范围求和Ⅱ **

给你一个 m x n 的矩阵 M ，初始化时所有的 0 和一个操作数组 op ，其中 ops[i] = [ai, bi] 意味着当所有的 0 <= x < ai 和 0 <= y < bi 时， M[x][y] 应该加 1。在 执行完所有操作后 ，计算并返回 矩阵中最大整数的个数 。
1

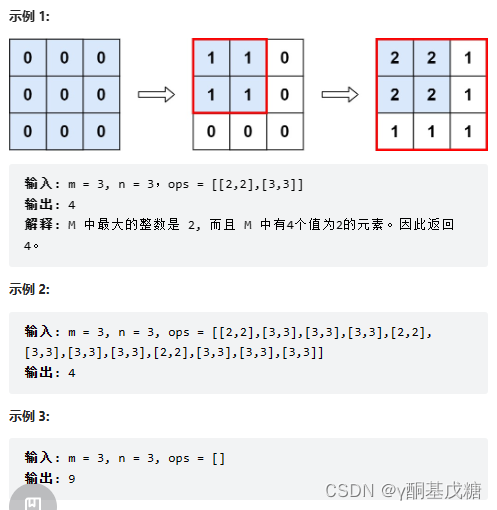
分析： 观察矩阵的元素变换情况，发现所求最大整数个数应该为操作数组OP中最小的x、y的乘积。
解法1： 见分析。
代码：

class Solution {
public:
    int maxCount(int m, int n, vector<vector<int>>& ops) {
        int a = m, b = n;
        for(auto & op : ops){
            a = min(a,op[0]);
            b = min(b,op[1]);
        }
        return a*b;
    }
};
1
2
3
4
5
6
7
8
9
10
11

思考：
理解vector构造的二维数组，op:ops就是访问ops中的每一个子项，如[2,2],[3,3]等，此时op就是一个一维数组。

419.甲板上的战舰

给你一个大小为 m x n 的矩阵 board 表示甲板，其中，每个单元格可以是一艘战舰 'X' 或者是一个空位 '.' ，返回在甲板 board 上放置的 战舰 的数量。战舰 只能水平或者垂直放置在 board 上。换句话说，战舰只能按 1 x k（1 行，k 列）或 k x 1（k 行，1 列）的形状建造，其中 k 可以是任意大小。两艘战舰之间至少有一个水平或垂直的空位分隔 （即没有相邻的战舰）。
1

分析： 根据题意，两艘战舰之间至少有一个空位，因此对于连续的一列或者一行就只能算一艘战舰。
解法1： 寻找战舰，之后将所在行或列的其他战舰全部标记为空。具体是对每个位置，向右、向下寻找是否有相邻的战舰，有的话就标记为空。
代码：

class Solution {
public:
    int countBattleships(vector<vector<char>>& board) {
        int m = board.size();
        int n = board[0].size();
        int num = 0;
        for(int i = 0; i < m; ++i){
            for(int j = 0; j < n; ++j){
                if(board[i][j] == 'X')
                {
                    board[i][j] = '.';
                    for(int k = i + 1; k < m && board[k][j] == 'X'; ++k){
                        board[k][j] = '.';
                    }
                    for(int q = j + 1 ; q < n && board[i][q] == 'X'; ++q){
                        board[i][q] = '.';
                    }
                    ++num;
                }
            }
        }
        return num;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

思考：
注意continue和break的区别，两者都有跳出循环的作用，但是还有区别。当有多层循环时，例如循环 if board[i][j]中，如果是break，则会执行board[i+1][j]，即跳出了上一层的循环，而continue则是执行board[i][j+1]，即结束本次循环开始下一个循环，不往上跳层。

        for(int i = 0; i < m; ++i){
            for(int j = 0; j < n; ++j){
                if(board[i][j] == 'X')
                {
                    ++num;
                    break;	//continue;
                }
            }
        }
1
2
3
4
5
6
7
8
9

五、数组的旋转

189.轮转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。
1

分析： 考虑一题多解。
解法1： 注意到数组轮转，其实是将数组元素向右移动k个位置，对于“溢出”的元素可以通过取余来更新位置。为了不在移动过程中改变数组元素，可以开辟一个数组来存储。
代码：

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
 int n = nums.size();
        vector<int> copy(n,0);
        for(int i = 0; i < n; i++){
            copy[(i+k)%n] = nums[i];
        }
        // for(int i = 0; i < n; ++i){
        //     nums[i] = copy[i];
        // }
        nums.assign(copy.begin(),copy.end());
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

思考：
注意assign的使用，将容器中的元素拷贝到另一个容器中。
解法2：

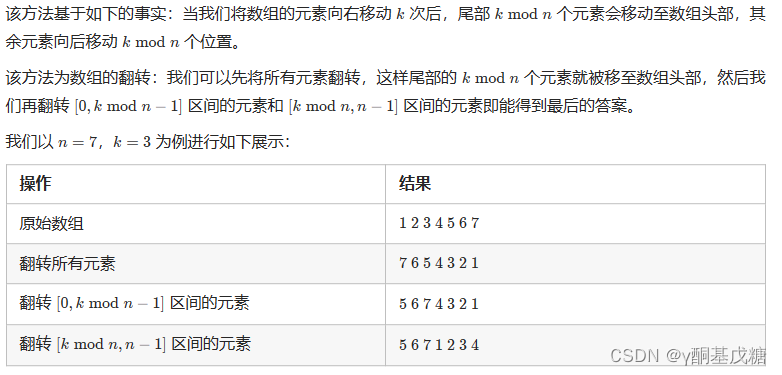
代码：

class Solution {
public:
    void reverse(vector<int>& nums, int start, int end) {
        while (start < end) {
            swap(nums[start], nums[end]);
            start += 1;
            end -= 1;
        }
    }

    void rotate(vector<int>& nums, int k) {
        k %= nums.size();
        reverse(nums, 0, nums.size() - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.size() - 1);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

思考：
类似于双指针的使用。
解法3： 环状替换：在不开辟新数组（复制）的情况下，只在原来的数组中复制更新，使用temp完成每一次的替换。

396.旋转函数

给定一个长度为 n 的整数数组 nums 。假设 arrk 是数组 nums 顺时针旋转 k 个位置后的数组，我们定义 nums 的 旋转函数  F 为：F(k) = 0 * arrk[0] + 1 * arrk[1] + ... + (n - 1) * arrk[n - 1]返回 F(0), F(1), ..., F(n-1)中的最大值 。生成的测试用例让答案符合 32 位 整数。
1

分析： 承接上题，首先想到的就是遍历各个k值下的f值，之后取较大值即可，但是最终报错耗时时间不通过；因此需要找规律来减少计算时间。
解法1： 找规律：
$$F(0)=0\ast arrk[0]+1\ast arrk[1]+2\ast arrk[2]+\dots \dots +(n-1)\ast arrk[n-1]$$
$$F(1)=0\ast arrk[n-1]+1\ast arrk[0]+2\ast arrk[1]+\dots \dots +(n-1)\ast arrk[n-2]$$
$$F(2)=0\ast arrk[n-2]+1\ast arrk[0]+2\ast arrk[1]+\dots \dots +(n-1)\ast arrk[n-2]$$
记原数组中所有元素和$$sumA=arrk[0]+arrk[1]+arrk[2]+\dots \dots +arrk[n-1]$$
则有下式成立：
$$F(i)=F(i-1)+sumA-n\ast arrk[n-i]$$
代码：

class Solution {
public:
    int maxRotateFunction(vector<int>& nums) {
        int n = nums.size(), sum = 0, f = 0;
        for(int i = 0; i < n; ++i){
            sum += nums[i];
            f += i*nums[i];
        }
        int res = f;
        for(int j = 1; j < n; ++j){
            f = f + sum - n*nums[n-j];
            res = max(res,f);
        }
        return res;
    }
};
// 遍历超时
// class Solution {
// public:
//     int RotateArr(vector<int>& nums, int k){
//         int n = nums.size();
//         int ret = 0;
//         for(int i = 0; i < n; ++i){
//             ret += ((i+k)%n)*nums[i];
//         }
//         return ret;
//     }
//     int maxRotateFunction(vector<int>& nums) {
//         int ans = INT_MIN;
//         for(int k = 0; k < nums.size(); ++k){
//             ans = max(ans,RotateArr(nums,k));
//         }
//         return ans;
//     }
// };
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

思考：
注意降低算法的复杂度，提高效率。

六、特定顺序遍历二维数组

54.螺旋矩阵 **

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。
1

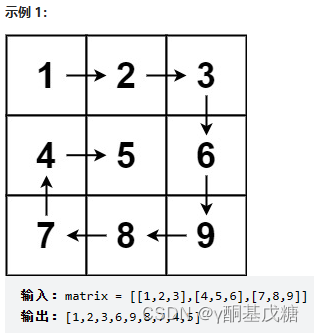
分析： 注意螺旋矩阵的输出顺序就是按层遍历，怎么设置转向条件才是关键。
解法1： 设立边界参数up, down, left, right，每到一个转角转向后更新边界，如+1、-1，这样矩阵最外层就被逐步剥离了。接下来就是转向的设计，从最外层开始，①从左向右遍历，碰到右边界为止，之后向下+1，若越过了下边界，说明已经遍历完成了；②从上向下遍历，碰到下边界为止，之后向左-1，若越过了左边界，说明已经遍历完成了；③从右向左遍历，碰到左边界为止，之后向上-1，若越过了上边界，说明已经遍历完成了；④从下向上遍历，碰到上边界为止，之后向右+1，若越过了右边界，说明已经遍历完成了。至此，实现了最外层的遍历，并进入第二层的遍历。
代码：

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        // 记录上下左右边界
        int up = 0, left = 0;
        int down = m - 1;
        int right = n - 1;
        // 输出数组
        vector<int> ret;

        // 输入数组为空数组
        if(matrix.empty())  return {};
        
        // 按层模拟
        while(true){
        // 向右遍历，到右边界为止
            for(int i = left; i <= right; ++i){
                ret.push_back(matrix[up][i]);
            }
        // 更新上边界，上面一排的数据就被丢弃了，如果上边界大于下边界，则遍历完成
            if(++up > down) break;
        // 向下遍历
            for(int j = up; j <= down; ++j){
                ret.push_back(matrix[j][right]);
            }
            if(--right < left) break;
        // 向左遍历
            for(int p = right; p >= left; --p){
                ret.push_back(matrix[down][p]);
            }
            if(--down < up) break;
        // 向上遍历
            for(int q = down; q >= up; --q){
                ret.push_back(matrix[q][left]);
            }
            if(++left > right) break;
        }
        return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

59.螺旋矩阵Ⅱ

给你一个正整数 n ，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
1

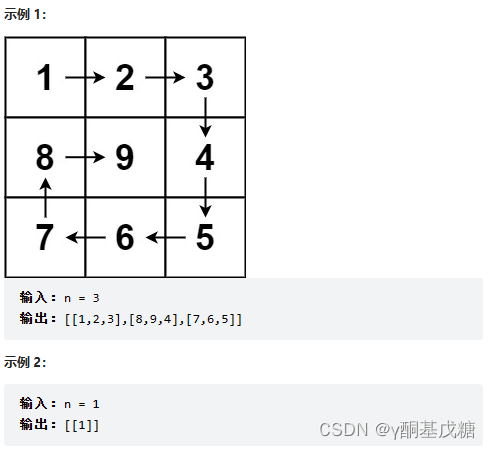
分析： 同上题。
解法1： 同上题。
代码：

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> ret(n,vector<int>(n));
        int up = 0, down = n-1, left = 0, right = n-1;
        int cnt = 1;
        while(true){
            for(int i = left; i <= right; ++i){
                ret[up][i] = cnt;
                ++cnt;
            }
            if(++up > down) break;
            for(int j = up; j <= down; ++j){
                ret[j][right] = cnt;
                ++cnt;
            }
            if(--right < left)  break;
            for(int p = right; p >= left; --p){
                ret[down][p] = cnt;
                ++cnt;
            }
            if(--down < up) break;
            for(int q = down; q >= up; --q){
                ret[q][left] = cnt;
                ++cnt;
            }
            if(++left > right)  break;
        }
        return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

498.对角线遍历 **

给你一个大小为 m x n 的矩阵 mat ，请以对角线遍历的顺序，用一个数组返回这个矩阵中的所有元素。
1

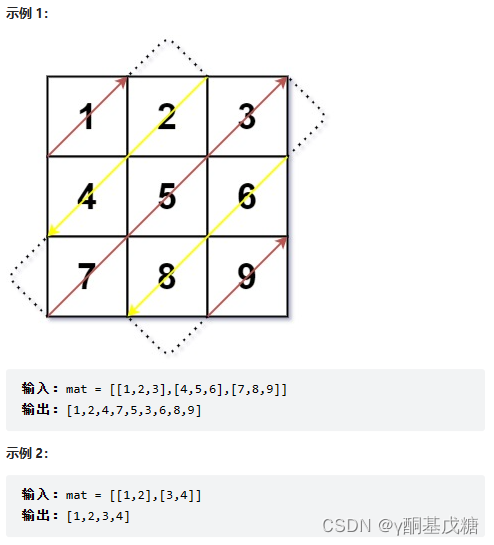
分析： 直接模拟，关键在于找规律：对角线遍历方向+遍历起点+边界条件。
解法1： 总共有$m+n-1$条对角线，$i\in [0,m+n-2],[m,n]=mat.shape()$；①若$i$为偶数，遍历起点：若$i<m$，为$(i,0)$，否则为$(m-1,i-m+1)$，遍历路径为：行减1，列加1；②若$i$为奇数，遍历起点：若$i<n$，为$(0,i)$，否则为$(i-n-1,n-1)$，遍历路径为：行加1，列减1。边界条件为数组边界，即遍历终点。
代码：

class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& mat) {
        int m = mat.size();
        int n = mat[0].size();
        vector<int> ret;
        for(int i = 0; i < m+n-1; ++i){
            if(i%2 == 0){
                int x = ( i < m ? i : m - 1 );
                int y = ( i < m ? 0 : i - m + 1 );
                while( x >= 0 && y < n){
                    ret.push_back(mat[x][y]);
                    --x;
                    ++y;
                }
            }
            else{
                int x = ( i < n ? 0 : i - n + 1 );
                int y = ( i < n ? i : n - 1 );
                while( x < m && y >= 0){
                    ret.push_back(mat[x][y]);
                    ++x;
                    --y;
                }
            }
        }
        return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

七、二维数组变换

566.重塑矩阵

在 MATLAB 中，有一个非常有用的函数 reshape ，它可以将一个 m x n 矩阵重塑为另一个大小不同（r x c）的新矩阵，但保留其原始数据。给你一个由二维数组 mat 表示的 m x n 矩阵，以及两个正整数 r 和 c ，分别表示想要的重构的矩阵的行数和列数。重构后的矩阵需要将原始矩阵的所有元素以相同的 行遍历顺序 填充。如果具有给定参数的 reshape 操作是可行且合理的，则输出新的重塑矩阵；否则，输出原始矩阵。
1

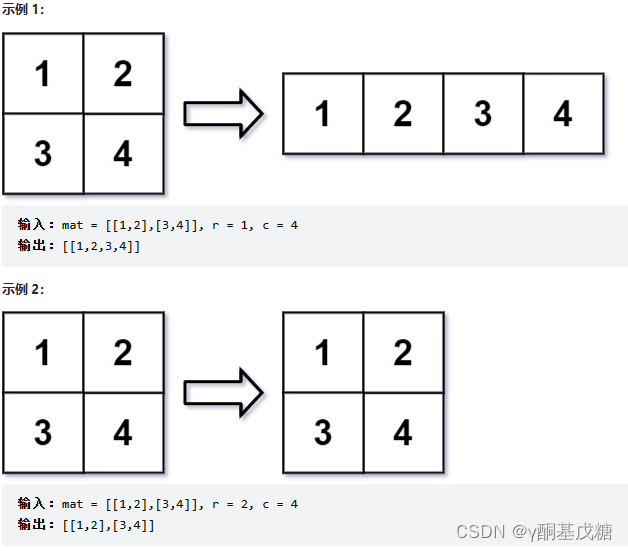
分析： 假设原矩阵$m\times n$中元素下标为$(x,y),x\in [0,m-1],y\in [0,n-1]$，到重塑矩阵$r\times c$中元素下标为$(i,j),i\in [0,r-1],j\in [0,c-1]$，应有等式成立$x\bullet n+y=i\bullet c+j$，则$x=(i\bullet c+j)/n,y=(i\bullet c+j)\%n$，这样就能直接赋值。
解法1： 见分析。
代码：

class Solution {
public:
    vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {
        int m = mat.size();
        int n = mat[0].size();
        if(m*n != r*c)  return mat;
        vector<vector<int>> ret(r,vector<int>(c));
        for(int i = 0; i < r; ++i){
            for(int j = 0; j < c; ++j){
                ret[i][j] = mat[(i*c+j)/n][(i*c+j)%n];
            }
        }
        return ret; 
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

解法2： 去掉一个循环，降低时间复杂度。
代码：

class Solution {
public:
    vector<vector<int>> matrixReshape(vector<vector<int>>& nums, int r, int c) {
        int m = nums.size();
        int n = nums[0].size();
        if (m * n != r * c) {
            return nums;
        }

        vector<vector<int>> ans(r, vector<int>(c));
        for (int x = 0; x < m * n; ++x) {
            ans[x / c][x % c] = nums[x / n][x % n];
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

思考：
注意时间复杂度。

48.旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
1

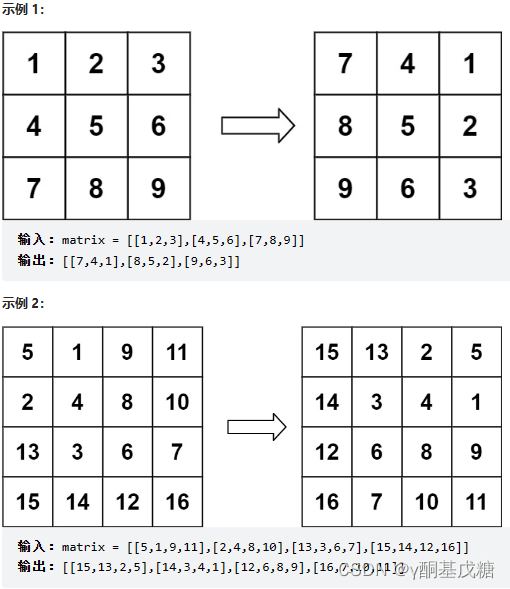
分析： 将矩阵块看成一个二维的骰子，观察顺时针旋转行元素的变化，可以得到结论：原矩阵中的第$i$行第$j$个元素，旋转后位于倒数第$n-i-1$列第$i$个元素。
解法1： 新建一个过渡数组，以不改变原数组的值。
代码：

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        vector<vector<int>> copy(n,vector<int>(n));
        for(int i = 0; i < n; ++i){
            for(int j = 0; j < n; ++j)
            {
                copy[j][n-i-1] = matrix[i][j];
            }
        }
        matrix.assign(copy.begin(),copy.end());
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

解法2： 原地旋转，降低空间复杂度。
①新建temp变量，发现旋转四次后元素回到原点，因此有以下原地旋转公式：
$temp=matrix[row][col]$
$matrix[row][col]=matrix[n-col-1][row]$
$matrix[n-col-1][row]=matrix[n-row-1][n-col-1]$
$matrix[n-row-1][n-col-1]=matrix[col][n-row-1]$
$matrix[col][n-row-1]=temp$
②确定遍历范围：当$n$为偶数时，需要遍历$n^2/4=(n/2)\ast (n/2)$个位置；当$n$为奇数时，需要遍历$(n^2-1)/4=(n-1)/2\ast (n-1)/2$个位置。

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < (n + 1) / 2; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

思考：
注意降低算法的空间复杂度，减少额外空间的使用。

73.矩阵置零

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
1

分析： 如果在寻找0元素的过程中将行和列设为0，会造成后面的误判。
解法1： 新建行、列标记数组，最后将涉及的行列元素都变为0。
代码：

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        vector<int> rowflag;
        vector<int> colflag;
        // 记录0元素所处的行、列
        for(int i = 0; i < m; ++i){
            for(int j = 0; j < n; ++j){
                if(matrix[i][j] == 0)
                {
                    rowflag.push_back(i);
                    colflag.push_back(j);
                }
            }
        }
        // 将所处行变为0
        for(int i = 0; i < rowflag.size(); ++i){
            for(int j = 0; j < n; ++j)
            matrix[rowflag[i]][j] = 0;
        }
        // 将所处列变为0
        for(int j = 0; j < colflag.size(); ++j){
            for(int i = 0; i < m; ++i){
                matrix[i][colflag[j]] = 0;
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

解法2： 将数组的第一行、第一列作为标记变量，有的话就将第一行、列对应元素置0，特别注意需要提前判断第一行、列是否存在0元素，防止置零时发生冲突。

289.生命游戏

根据 百度百科 ， 生命游戏 ，简称为 生命 ，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。
给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：
1.如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
2.如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
3.如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
4.如果死细胞周围正好有三个活细胞，则该位置死细胞复活；
下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。
1
2
3
4
5
6
7

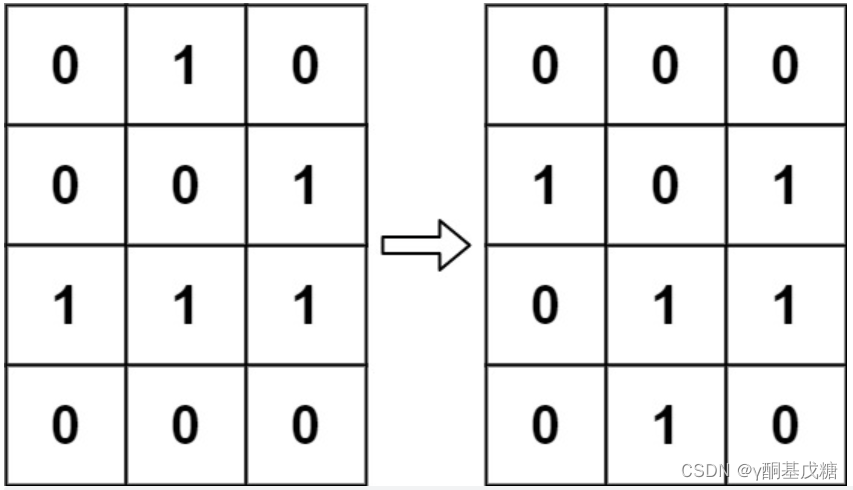
分析： 按照题述条件设置翻转条件即可。
解法1： 为了防止反转后改变原数组的值，设置一个状态矩阵flag。然后每个元素设置滑窗，根据规则计算flag状态，1或者0。
代码：

class Solution {
public:
    void gameOfLife(vector<vector<int>>& board) {
        int m = board.size();
        int n = board[0].size();
        vector<vector<int>> flag(m, vector<int>(n));
        // 标记需要翻转状态的元素
        for(int i = 0; i < m; ++i){
            for(int j = 0; j < n; ++j){
                if(board[i][j] == 1)
                {
                    int cnt = 0;
                    // 创建滑窗
                    for(int x = i - 1; x <= i + 1; ++x){
                        for(int y = j - 1; y <= j + 1; ++y){
                            if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 1)
                            ++cnt;
                        }
                    }
                    if(cnt < 3 || cnt > 4)    flag[i][j] = 1;
                }
                else
                {
                    int cnt = 0;
                    for(int x = i - 1; x <= i + 1; ++x){
                        for(int y = j - 1; y <= j + 1; ++y){
                            if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 1)
                            ++cnt;
                        }
                    }
                    if(cnt == 3)    flag[i][j] = 1;
                }
            }
        }
        // 反转元素
        for(int i = 0; i < m; ++i){
            for(int j = 0; j < n; ++j){
                if(flag[i][j] == 1 && board[i][j] == 0)
                    board[i][j] = 1;
                else if(flag[i][j] == 1 && board[i][j] == 1)
                    board[i][j] = 0;
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

解法2： 为了防止元素的更新影响后续的判断，可以将反转后的状态改为符合状态，即0和1外的其他元素。举个例子，如果细胞之前的状态是 0，但是在更新之后变成了 1，我们就可以给它定义一个复合状态 2。这样我们看到 2，既能知道目前这个细胞是活的，还能知道它之前是死的。
思考：
注意复合状态的思路，在避免元素更新带来的冲突上的应用。

八、前缀和数组

303. 区域和检索 - 数组不可变 **

给定一个整数数组  nums，处理以下类型的多个查询:
计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的 和 ，其中 left <= right
实现 NumArray 类：
NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + ... + nums[right] )
1
2
3
4
5

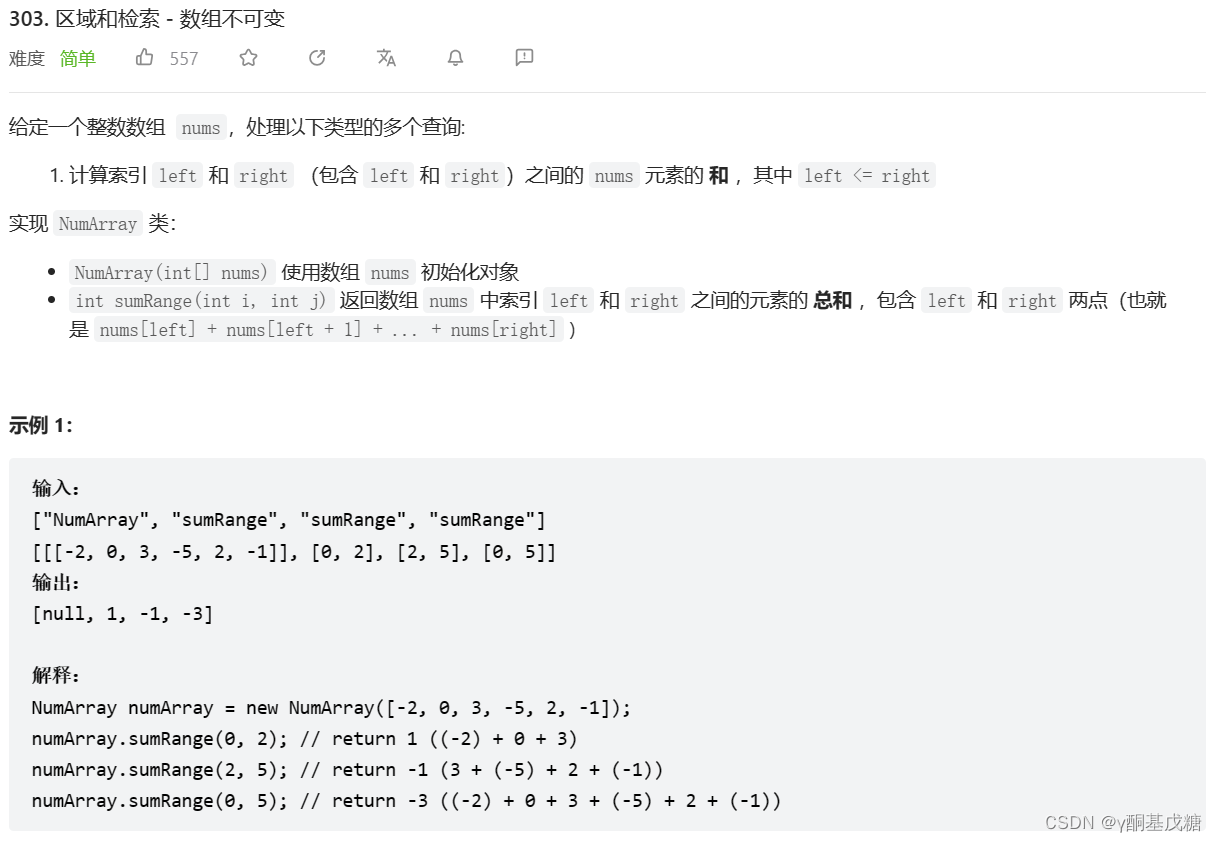
分析： 考查前缀和。前缀和的理解：求解数组[1 2 3 4 5 6 7 8 9 10]的前1、2、3、4、……、10个元素的和，一般的解法是分别求1、1+2、1+2+3、1+2+3+4、……、1+2+3+……+9+10，前缀和的解法，sum1、sum2 = sum1 + 2、sum3 = sum2 + 3、sum4 = sum3 + 4、……、sum10 = sum9 + 10。
解法1： 应用前缀和求解。为了避免出现-1的下标，sum大小为n+1，n为原数组元素个数，数组的前 j 项和对应sum[j+1]，相当于外后一格。
代码：

class NumArray {
public:
    vector<int> sum;
    NumArray(vector<int>& nums) {
        int n = nums.size();
        sum.resize(n+1);
        for(int i = 0; i < n; ++i){
            sum[i+1] = sum[i] + nums[i];
        }
    }
    
    int sumRange(int left, int right) {
        return sum[right+1] - sum[left];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

思考：
注意前缀和的使用。

304. 二维区域和检索 - 矩阵不可变

给定一个二维矩阵 matrix，以下类型的多个请求：
计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。
实现 NumMatrix 类：
NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。
1
2
3
4
5

分析： 考查前缀和。
解法1： 对行应用前缀和，一维的前缀和数组。
代码：

class NumMatrix {
public:
    vector<vector<int>> sum;
    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        sum.resize(m,vector<int>(n + 1));
        for(int i = 0; i < m; ++i){
            for(int j = 0; j < n; ++j){
                sum[i][j+1] = sum[i][j] + matrix[i][j];
            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        int retsum = 0;
        for(int i = row1; i <= row2; ++i){
            retsum += (sum[i][col2+1]-sum[i][col1]);
        }
        return retsum;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

解法2： 对行列一起应用前缀和，二维的前缀和数组，根据相交的区域进行加减的理解。

class NumMatrix {
    int[][] sums;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        if (m > 0) {
            int n = matrix[0].length;
            sums = new int[m + 1][n + 1];
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    sums[i + 1][j + 1] = sums[i][j + 1] + sums[i + 1][j] - sums[i][j] + matrix[i][j];
                }
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return sums[row2 + 1][col2 + 1] - sums[row1][col2 + 1] - sums[row2 + 1][col1] + sums[row1][col1];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

238.除自身数组以外的乘积

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在  32 位 整数范围内。请不要使用除法，且在 O(n) 时间复杂度内完成此题。
1

分析： 题目提到不要使用除法，那么只能使用乘法来计算。时间复杂度为n，意味着数组遍历只能套一个循环。
解法1： 分别计算左侧前缀和及右侧后缀和，两者相乘便是所求的乘积。
代码：

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n = nums.size();
        vector<int> leftarr(n+1,1);
        vector<int> rightarr(n+1,1);
        vector<int> ret(n);
        for(int i = 0; i < n; ++i){
            leftarr[i+1] = leftarr[i] * nums[i];
            rightarr[i+1] = rightarr[i] * nums[n-1-i];
        }
        for(int j = 0; j < n; ++j){
            ret[j] = leftarr[j]*rightarr[n-1-j];
        }
        return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

写在最后

听听我的故事吧。

我是一枚从事自动驾驶点云处理方向的研一学生，只有一个快90岁的院士老师，几乎是完全散养。研一上明确自己要读博，开始准备科研成果+项目，不过课程较多最后只产出了2篇发明专利。进入研一下，节奏完全变化，2月开学准备考试，3月初被告知最爱的妈妈得了癌症，晚期且手术已经做完，动身去北京。之后3-5月初两个月暂时停滞了我的脚步，两个月里开始跑北京、杭州、长春、安庆等地的医院，化疗、问诊，算是开始了医学的一些调研，写了一些文章和总结，推翻了北京301给的治疗方案，确定了后续几个月的化疗和维持治疗方案。然后爸爸也生病了，开始看精神科、心理科医生，加住院检查治疗。两个月里经历了妈妈癌症晚期检测及治疗、爸爸重度焦虑抑郁、女朋友和我分手，生命中最重要的前三个人同时倒下或离开，我也改变了未来的规划——工作和结婚。

5月初忙完妈妈的第三次化疗和爸爸的治疗，回到长春开始人生的新阶段。虽说是过来的，但是家里的事我依旧放不下，很多时间还是在调研妈妈的治疗，以及和医生、病友交流。因为要工作，所以准备开始刷力扣，到今天为止，大概1个月，才刷了30+题目，最后7道是在这两天刷完的，至此数组篇完整结束。我也终于开始重建我的生活和工作，今天的我终于像是回到了三个月开学初的那段日子，我一直没倒下，这次反而挺的更直。

陌生人，我想说，你们一定要努力再努力、且行且珍惜。而我，也将继续开始我的另一段路，继续刷题。我可以，你也可以，共勉！
2023.06.09